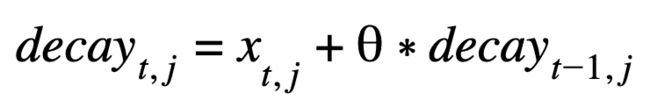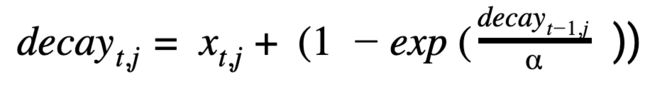Robyn MMM2.0 - Facebook Marketing Science（R）市场营销-广告投放

代码链接： https://github.com/facebookexperimental/Robyn

教学使用视频：https://www.youtube.com/watch?v=aIiadcfL4uw

目录

1 原文翻译部分：

1.1 快速开始

1.2 使用进化算法进行模型选择

1.3 商业真实使用情况

1.4 分步指南

1.4.1 库

1.4.2 为 Nevergrad 创建、安装和使用 conda 环境

1.4.3 加载数据

1.4.4 设置国家

1.4.5 日期变量

1.4.6 因变量

1.4.7 设置 Prophet 变量

1.4.8 设置基线变量

1.4.9 设置渠道名

1.4.10 设置因子变量

1.4.11 设置超参数界限的指南

 1.4.12 各模型输出结果

1.4.13 预算优化器

2 部分原理说明

2.1 岭回归

2.2 变量变换

2.3 Facebook Prophet - 趋势、季节性和假期影响

2.4 自动超参数选择和优化

2.5 使用实验结果校准

 2.6 输出和分析

2 常见问题及注意事项

2.1 常见问题

2.2 注意事项（含csv变量解释）

---

简介：Robyn 是 Facebook Marketing Science 的实验性、自动化和开源营销组合建模 (MMM) 代码。它使用各种机器学习技术（带交叉验证的岭回归、用于超参数优化的多目标进化算法、用于预算分配的基于梯度的优化等）

1 原文翻译部分：

1.1 快速开始

1. 获取 .R 脚本

• 有三个 .R 脚本文件：
  • fb_robyn.exec.R # 你只需要执行这个脚本，它会调用其他 2 个脚本
  • fb_robyn.func.R # 包含特征工程、建模功能和绘图
  • fb_robyn.optm.R # 这包含预算分配器和绘图
• 两个 .csv 文件作为示例数据：
  • de_simulated_data.csv # 这是我们的模拟数据集。
  • Generated_holidays.csv # 这包含了从图书馆来的所有国家的假日先验。请检查你的国家是否包括在内，如果所有的假期都包括在内。还建议在该表中添加额外的活动，例如学校假期。
• 所有文件必须放在同一个文件夹中

2. R 版本和库

• 强烈建议更新到 R 版本 4.0.3 以避免潜在错误
• 请确保您首先安装了 fb_robyn.exec.R 中指定的所有库
• 还请安装 Anaconda for reticulate。简单指令请查看库部分中的 fb_robyn.exec.R
• 对于 Windows，如果您收到 openssl 错误，请参阅此处和此处的说明以安装和更新 openssl

3. 使用样本数据进行试

运行

• 请按照 fb_robyn.exec.R 中的所有说明进行操作

• 完成上述步骤后，如果您全选并在 fb_robyn.exec.R 中运行，脚本应执行 20k 次迭代（500 次迭代 * 40 次试验）并在您选择的文件夹中保存一些图

• 一个示例模型 输出分析图 看起来像这样：

• 最后一个函数 f.budgetAllocator() 可能会抛出错误“如果 ModID 不在最佳结果范围内”。首先，请阅读函数后面的所有说明。模型 ID 编码在每个 onepager .png 名称和标题中。此外，执行 model_output_collect$allSolutions 将输出所有最终模型 ID。请挑一个放入f.budgetAllocator()。

• 优化模型示例如下所示：

1.2 使用进化算法进行模型选择

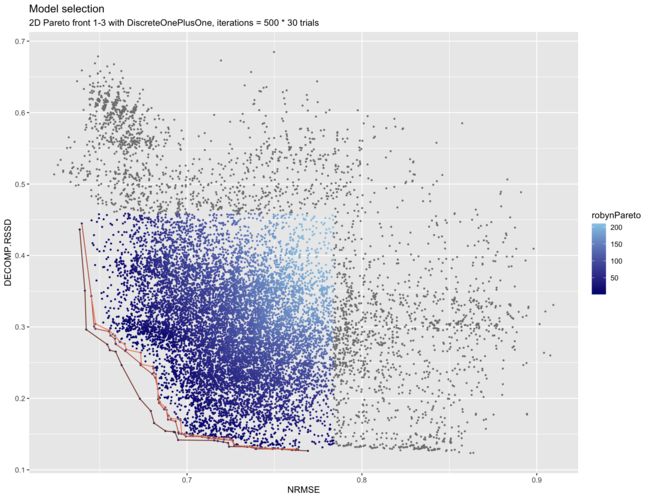
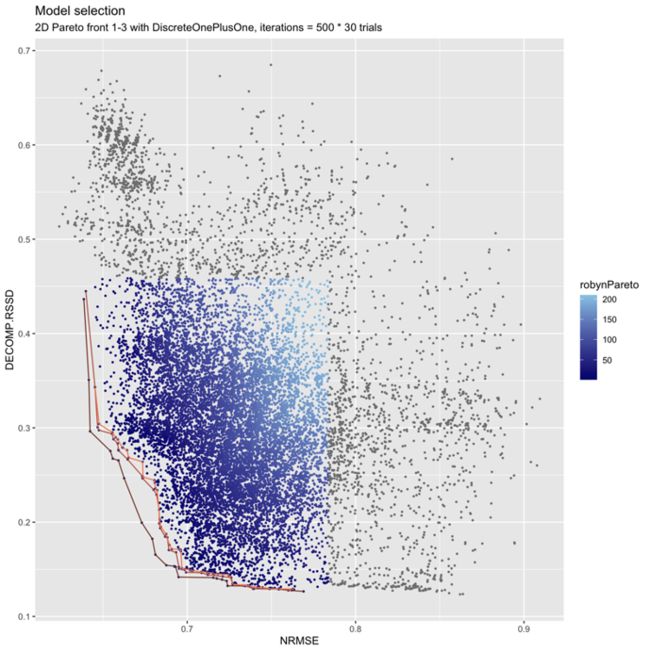
使用 Facebook AI 的开源无梯度优化库Nevergrad，Robyn 能够利用进化算法执行多目标超参数优化并输出一组帕累托最优解。除了 NRMSE 作为优化的损失函数之外，Robyn 还最小化了业务逻辑“分解距离”，或 DECOMP.RSSD，旨在引导模型朝着更真实的分解结果发展。在校准的情况下，还会添加第三个损失函数 MAPE.LIFT。

下图展示了 NRMSE 和 DECOMP.RSSD 上典型的帕累托前沿 1-3：

1.3 商业真实使用情况

1 Resident

Resident拥有几个网上品牌的家居用品，主要是床垫。该公司的主要品牌是 Nectar 和 DreamCloud，这两个品牌在美国和英国都有在线销售，在美国各地有2500多家门店。

目标：面对冠状病毒 (COVID-19) 大流行带来的变化，再加上在线生态系统 (iOS 14) 的发展使得衡量其广告效果变得更加困难，Resident 正在寻找一种强大的解决方案来衡量其所有广告的表现。营销渠道，以优化预算​​分配并最大化在线销售。

结果：使用 Facebook Robyn 的决定产生了令人信服的回报。自 2020 年 12 月以来，该公司一直在使用 Robyn 来为预算分配决策提供信息，并因此增加了其 Facebook 支出的份额。优化工作取得了：

• 在每次收购的混合成本相同的情况下，收入增加 20%
• 实施 Robyn 模型需要 5 天（相比实施其内部模型需要 5 个工作月）

2 Central Group

作为 Central Group 集团的一部分，Central Retail Corporation (CRC) 是泰国领先的多业态、多类别全渠道零售平台，业务垂直领域包括时尚和生活方式、食品、房地产和强硬商品。它经营着广泛的零售业务，从百货商店到电子商务平台，在泰国拥有 3,000 多个销售点。

目标：为了更好地了解其营销活动对跨多个数字渠道的销售和广告支出回报的结果，CRC 需要一种经济高效的方法来衡量每个渠道。

结果：在与 Robyn 进行营销组合建模研​​究后，CRC 获得了有关如何增加收入的令人信服的见解，并计划在 2021 年全年为其其他业务部门进行 Robyn 支持的研究。结果包括：

• 广告支出的第二高回报来自 Facebook（来源：Robyn 营销组合建模研​​究）
• 17% 的总收入来自 Facebook（来源：Robyn 营销组合建模研​​究）
• 通过重新分配预算，收入可能增加 28%（来源：Robyn 营销组合建模研​​究）

1.4 分步指南

1.4.1 库

首先，在运行代码之前安装并加载所有包。您将使用几个开源包来运行它。您会发现几个与使用数据表、循环、并行计算和绘制结果相关的包。然而，核心回归过程的主要包是“glmnet”，岭回归将从中执行。另一个重要的包是“reticulate”，它为 Python 和 R 之间的互操作性提供了一套全面的工具，并且是能够使用Nevergrad算法的关键。

library(glmnet)
library(reticulate)
...
...

1.4.2 为 Nevergrad 创建、安装和使用 conda 环境

安装并加载所有软件包后，您将需要执行以下命令，以便在 reticulate 上创建、安装和使用 conda 环境。这是能够使用使用 Python 的 Nevergrad 算法所必需的：

conda_create("r-reticulate") #must run this line once only
conda_install("r-reticulate", "nevergrad", pip=TRUE) #must install nevergrad in conda before running Robyn
use_condaenv("r-reticulate")

1.4.3 加载数据

首先，您将加载包含的模拟数据并创建结果变量。与在任何 MMM 中一样，这是一个数据框，其中包含一组最小的 ds 和 y 列，分别包含日期和数值。您可能还想添加解释变量来说明不同的营销渠道及其投资、印象或任何其他指标，以确定营销活动的规模和影响。请记住，此自动文件读取解决方案要求您使用 RStudio 并将您的工作目录设置为 Rstudio 中的源文件位置：

#### load data & scripts

script_path <- str_sub(rstudioapi::getActiveDocumentContext()$path, start = 1, end = max(unlist(str_locate_all(rstudioapi::getActiveDocumentContext()$path, "/"))))
dt_input <- fread(paste0(script_path,'de_simulated_data.csv')) # input time series should be daily, weekly or monthly
dt_holidays <- fread(paste0(script_path,'holidays.csv')) # when using own holidays, please keep the header c("ds", "holiday", "country", "year")

source(paste(script_path, "fb_robyn.func.R", sep=""))
source(paste(script_path, "fb_robyn.optm.R", sep=""))

1.4.4 设置国家

要声明的第一个变量是国家/地区。我们建议仅使用一个国家/地区，特别是如果您打算利用先知来了解趋势和季节性，它会自动为您选择的国家/地区拉取假期并简化流程。在模拟数据下，我们使用“DE”作为示例国家。

set_country <- "DE" # only one country allowed. Used in prophet holidays

1.4.5 日期变量

set_dateVarName

对于日期变量，您必须牢记数据集中的 DATE 列必须采用“yyyy-mm-dd”格式。如“2020-01-01”

请注意，如果数据集时序是week为单位时：在中文语言win系统里，系统检测识别日期间隔部分，对于日期返回的是中文的星期一或者星期天所以在fb_robyn.func.R文件的463行改成中文

weekStartMonday <- if(weekStartInput=="星期一") {TRUE} else if (weekStartInput=="星期天") {FALSE} else {stop("week start has to be Monday or Sunday")}

set_dateVarName <- c("DATE") # date must be format "2020-01-01"

1.4.6 因变量

set_depVarName 和 set_depVarType 
设置因变量基本上是您要测量的结果。我们只接受 set_depVarName 下的一个因变量。此变量可以采用收入（销售额或货币价值的利润）或转换（交易数量、销售单位）的形式，您将在定义 set_depVarType 变量时指明。

set_depVarName <- c("revenue") # there should be only one dependent variable
set_depVarType <- "revenue" # "revenue" or "conversion" are allowed

1.4.7 设置 Prophet 变量

activate_prophet 
首先，如果您想在代码中打开或关闭用于季节性、趋势和假期的Prophet功能，您需要指明模型。T（真）表示已激活，F（假）表示停用。Prophet 实现了一个基于可加模型预测时间序列数据的程序，其中非线性趋势与每年、每周和每天的季节性以及假日效应相吻合。它最适用于具有强烈季节性影响和多个季节历史数据的时间序列。Prophet 对缺失数据和趋势变化具有稳健性，并且通常可以很好地处理异常值。

activate_prophet <- T

set_prophet #
下一步是选择您将在模型中使用 Prophet 提供的哪些结果。建议至少保持趋势和假期。请记住，提供了“趋势”、“季节”、“工作日”、“假日”并区分大小写。有关每个选择将执行的操作的更多详细信息，请查看Prophet 包的CRAN 文档，了解功能 - 假期、每年.季节性、每周.季节性、每日.季节性。最佳做法是至少包括“趋势”和“假期”。

set_prophet <- c("trend", "season", "holiday")

set_prophetVarSign #

您可以将先知变量的变量符号控制定义为“默认”、“正”或“负”。如果您期望诸如“趋势”、“季节”、“假期”等先知变量的系数为默认值（正或负）、正或负。我们建议使用默认值让先知有机会检测响应变量中的正面或负面整体影响。在某些情况下，您可能想要控制标志。例如，假设您已经知道，由于业务现实和其他您无法控制的因素（例如经济危机），总体销售增长趋势正在下降。因此，您可能希望指示算法仅查找趋势和销售额之间的负相关关系以反映这种情况。

set_prophetVarSign <- c("default","default", "default")

1.4.8 设置基线变量

接下来的步骤是设置基准变量，这些变量通常是竞争对手、定价、促销、温度、失业率和任何其他不是媒体曝光但与销售结果有密切关系的变量。如果要在代码中打开或关闭基线变量，则需要指明模型。T（真）表示已激活，F（假）表示停用。在大多数情况下，应该有一些非媒体变量会对您的因变量产生影响，因此创建这些基线变量很重要。

activate_baseline <- T

然后，您可以定义要考虑的不同基线变量。这些应该是数据文件中列的名称。

set_baseVarName <- c("promotions", "price changes", "competitors sales")

您可以将基线变量的符号控制应用为“默认”、“正”或“负”。如果您期望基线变量（例如“促销”、“价格变化”、“竞争对手的销售额”）的系数为默认值（正或负）、正或负，具体取决于其与因变量的预期关系。例如，下雨天气可能对销售产生正面或负面影响，具体取决于业务。请记住声明的对象必须与 set_baseVarName 的长度相同

set_baseVarSign <- c("negative",’default’,’negative’) #“positive” is the remaining option

1.4.9 设置渠道名

set_mediaVarName 和 set_mediaSpendName

这里要记住一个关键限制，您必须为要衡量的每个媒体渠道声明支出变量。因此，它们必须与设置的mediaVarName 变量的顺序和长度相同。如果数据可用于除支出变量之外还包括展示次数/GRP/等（非支出变量），请使用 set_mediaVarName 中的非支出变量，并确保变量名称不使用“ S”（下划线 S ) 命名约定。我们想同时使用这两个变量的原因是，非支出变量是衡量风险的一个指标，无论它们的成本是多少。支出和非支出变量可能具有复杂的关系，并且通常会根据众多因素而波动，因此使用更直接代表媒体曝光度的变量非常重要。

正确的

set_mediaVarName <- c("tv_S"    ,"ooh_S",   "print_S"   ,"facebook_I"   ,"search_clicks_P")

set_mediaSpendName <- c("tv_S"  ,"ooh_S",   "print_S"   ,"facebook_S"   ,"search_S")

错误的

set_mediaVarName <- c("tv_S"    ,"ooh_S",   "print_S"   ,"facebook_I"   ,"search_clicks_P")

set_mediaSpendName <- c("tv_S"  ,"ooh_S",   "print_S")

set_mediaVarSign 
您可以将媒体变量的符号控制应用为“默认”、“正”或“负”。如果您希望基线变量（例如“tv”、“print”、“facebook”）的系数为默认值（正数或负数）、正数或负数，具体取决于其与因变量的预期关系。我们建议对所有人使用正数，因为媒体应该对您的因变量产生积极影响。请记住声明的对象必须与 set_mediaVarName 的长度相同

1.4.10 设置因子变量

如果上面的任何变量应该是因子类型，请将其包含在这部分代码中，否则将其置空，因为默认情况下" c() "将是这种类型的变量是具有定性数据的变量。

set_factorVarName <- c()

1.4.11 设置超参数界限的指南

该超参数范围，我们建议保留为默认值，但可以根据从模型迭代和分析师们以往的经验学习收获来改变。

1. 每个超参数的定义：

   1. Thetas：几何函数衰减率。例如，如果模型的时间单位是每周，它将代表每周结转到下周的效果百分比。

   2. Shapes : Weibull 参数，控制指数和 S 形之间的衰减形状。越大越S形，越小越L形。

   3. Scales：控制衰减拐点位置的威布尔参数。推荐的界限在 0 到 0.1 之间。这是因为规模可以显着增加库存半衰期。

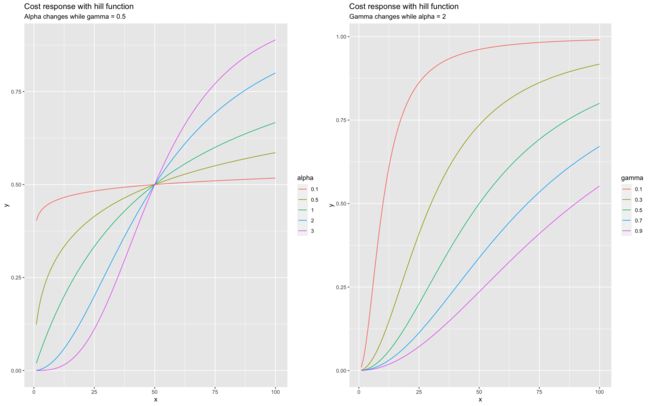
   4. Alphas：Hill 函数（收益递减）参数，控制指数和 S 形之间的形状。alpha 越大，S 形越多。越小，越C形。

   5. Gammas：控制拐点的 Hill 函数（收益递减）参数。伽马越大，响应曲线中的拐点越晚。

2. 了解广告素材如何影响媒体转型：

   1. 为了做出更明智的决定来定义超参数值，在媒体变量转换期间了解哪个超参数在做什么是非常有帮助的。绘图函数 f.plotAdstockCurves 可帮助您准确理解这一点。
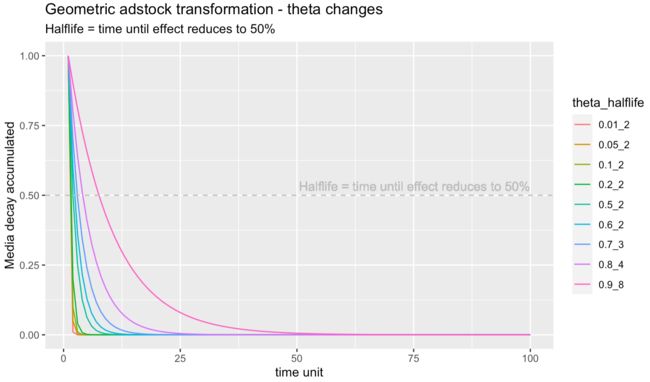
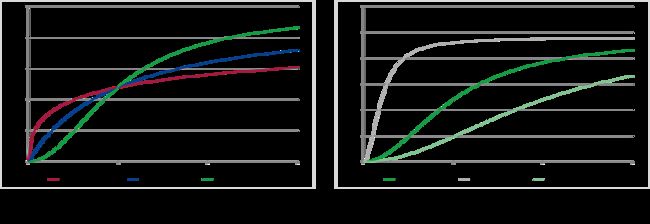
   2. 下面我们可以找到一个几何广告库存函数具有不同 theta 值的示例。您可能会观察到这是一个单参数 (theta) 函数。假设时间单位是周，我们可以看到当theta为0.9时，意味着每周90%的媒体效应会延续到下周。8 周后达到广告半衰期（图例中的半衰期值）。换句话说，当 theta = 0.9 时，媒体效应衰减到一半需要 8 周时间。这应该可以帮助您对 theta 的值有更切实的感觉，以及它们是否对某些渠道有意义。

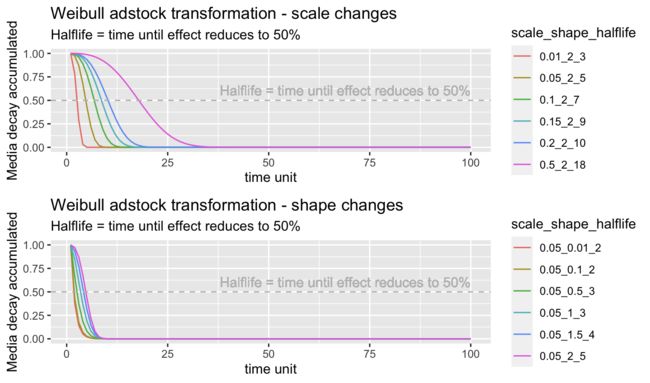
与上面的几何函数类似，威布尔图将威布尔函数的两个参数（尺度和形状）可视化。上图显示了在保持形状不变的情况下比例的变化。我们可以观察到，尺度越大，拐点越晚。当 scale=0.5 和 shape = 2 时，媒体效应衰减到一半需要 18 周（参见图例）。下图显示了在保持比例不变的情况下形状的变化。当形状较小时，曲线反而呈 L 形。当形状较大时，曲线反而变成倒S形。

以下要设置的媒体转换边界是 Hill 函数（收益递减）曲线比例和形状参数。收益递减理论认为，每增加一个广告单位，响应就会增加，但速度会下降。这一关键的营销原则在营销组合模型中体现为一种变量转换。当更改每个通道的 alpha 和 gamma 参数值范围时，您可能会在下方观察到收益递减曲线的差异。alpha 值越高，S 形越多，α 值越低，C 形越多。建议的范围介于 0.5 和 3 之间，以便提供对营销变量有意义的合理曲线。然而，伽马值越高，拐点出现的时间就越晚。 

 1.4.12 各模型输出结果

完成所有试验和迭代后，模型将继续绘制不同的图表，这些图表将帮助您根据 NRMSE 和媒体变量分解质量得分评估营销渠道贡献的最佳模型。您可以在“运行模型”步骤中设置的 plot_folder 中找到所有模型图，如下例所示。您将看到文件夹中保存的每个模型和图表都有一个模型唯一 ID。在下面的示例中，mod_ID = 1_22_3。

1.4.13 预算优化器

预算分配器也称为优化器。它提供了最佳媒体组合，在满足一组约束条件的同时，最大限度地提高了特定支出水平的回报。请注意，只有当 MMM 结果有意义时，预算分配器才会输出合理的优化，这意味着所有媒体渠道都已经为广告投放和 S 曲线找到了合理的超参数，并且每个渠道的响应都符合您的期望。否则，预算分配器输出是不可解释的。从技术上讲，预算分配器消耗 MMM 结果提供的每个通道的响应曲线（Hill函数），并进行求解器进行非线性优化。选择基于梯度的算法（用于全局优化的增强拉格朗日/AUGLAG 和用于局部优化的移动渐近线方法/MMA）来解决具有相等和不等约束的非线性优化问题。详情见在这里。

您必须定义的第一件事是来自上一部分结果的模型唯一 ID，您希望将其用于优化器。继续上面的示例，设置modID = "1_22_3"可以是从“model_output_collect$allSolutions”结果对象中的最佳模型列表中选择的模型的示例。

optim_result <- f.budgetAllocator(modID = "1_22_3"
                                ...
                                ...
)

我们当前的预算分配器有两种情况：

• 最大历史响应（max_historical_response）：假设使用五个媒体渠道的两年数据来构建模型。总支出为 1 MM 欧元，两个渠道均分为 40/30/15/10/5，总回报为 2 MM 欧元。预算分配器将输出历史支出水平 1MM€ 的最佳分割。例如，将花费的 1 MM 欧元分成 35/25/20/12/8 份，可以获得 2.5MM 的最大回报。

optim_result <- f.budgetAllocator(
                            modID = "1_22_3"
                          , scenario = "max_historical_response"
                            ...
                            ...
)

• 预期支出的最大响应（max_response_expected_spend）：与上述相比，该场景输出的是特定支出水平的最佳支出分配，而不是历史支出水平。例如，如果您下个季度有 100k€，您可以定义 expected_spend = 100000 和 expected_spend_days = 90。

optim_result <- f.budgetAllocator(
                            modID = "1_22_3"
                          , scenario = "max_response_expected_spend"
                            ...
                            ...
)

对于这两种情况，您还必须使用参数 channel_constr_low 和 channel_constr_up 为每个通道定义约束（下限和上限）。假设您在频道 A 上平均每周花费 10k€，那么 channel_constr_low = 0.7 和 channel_constr_up = 1.2 将不允许优化器在运行优化时为频道 A 低于 7k€ 或高于 12k€。一般情况下，请使用现实场景，避免设置太极端的值。预算分配器仍基于您的历史业绩。例如，如果您投入的金额是历史支出的 10 倍，则预算分配器结果可能没有意义。

optim_result <- f.budgetAllocator(
                            modID = "1_22_3"
                          , scenario = "max_historical_response" # c(max_historical_response, max_response_expected_spend)
                          , channel_constr_low = c(0.7, 0.75, 0.60, 0.8, 0.65) # must be between 0.01-1 and has same length and order as set_mediaVarName
                          , channel_constr_up = c(1.2, 1.5, 1.5, 2, 1.5) # not recommended to 'exaggerate' upper bounds. 1.5 means channel budget can increase to 150% of current level
)

结果如下所示。再次强调，预算分配器的结果只有在所选模型结果有意义时才能解释。

2 部分原理说明

2.1 岭回归

为了解决许多回归量之间的多重共线性并防止过度拟合，我们应用正则化技术以引入一些偏差为代价来减少方差。这种方法倾向于提高 MMM 的预测性能。最常见的正则化，我们在这段代码中使用的是岭回归。岭回归的数学符号是：

如果我们更深入地了解我们将在模型规范中使用的实际组件，除了上面的 lambda 惩罚项之外，我们还可以确定以下公式：

在我们执行此部分的代码下方，请记住您会在“func.R”脚本下找到它：

        #####################################
        #### fit ridge regression with x-validation
        cvmod <- cv.glmnet(x_train
                           ,y_train
                           ,family = "gaussian"
                           ,alpha = 0 #0 for ridge regression
                           ,lower.limits = lower.limits
                           ,upper.limits = upper.limits
                           ,type.measure = "mse"
        )

2.2 变量变换

代码中有两个主要的变量转换：

1. 广告影响衰减
2. 收益递减

2.2.1 广告影响衰减

这种技术对于更好、更准确地表示营销活动的实际结转效果非常有用。此外，它有助于提高对衰减效应的理解以及如何将其用于运动规划。它反映了广告效果在初次曝光后会滞后和衰减的理论。换句话说，并不是所有的广告效果都能立即感受到——记忆力会增强，人们有时会推迟行动——这种意识会随着时间的推移而减弱。

您可以从代码中选择两种广告技术：

1. 几何：传统上使用指数衰减函数，并在由 theta 控制的数据上使用衰减参数。例如，theta = 0.75 的广告素材意味着第 1 期中 75% 的展示被带到第 2 期。在数学上，传统的指数广告素材衰减效应定义为：

 您将在下面的代码中找到 adstock 几何函数。请记住，所有函数都位于“func.R”脚本中。

#### Define adstock geometric function
f.adstockGeometric <- function(x, theta) {
  x_decayed <- c(x[1] ,rep(0, length(x)-1))
  for (xi in 2:length(x_decayed)) {
    x_decayed[xi] <- x[xi] + theta * x_decayed[xi-1]
  }
  return(x_decayed)
}

 2.Weibull：Weibull 生存函数（Weibull 分布）在分布的形状和尺度上提供了更大的灵活性。公式定义为：

#### Define adstock weibull function
f.adstockWeibull <- function(x, shape , scale) {
  x_bin <- 1:length(x)
  x_decayed <- c(x[1] ,rep(0, length(x)-1))
  for (xi in 2:length(x_decayed)) {
    theta <- 1-pweibull(x_bin[xi-1], shape = shape, scale = scale)
    x_decayed[xi] <- x[xi] + theta * x_decayed[xi-1]
  }
  return(x_decayed)
}

 2.2.2 收益递减

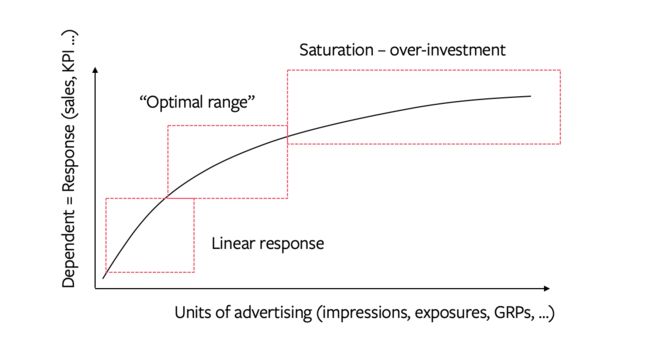
收益递减理论认为，每增加一个广告单位，响应就会增加，但速度会下降。这一关键的营销原则在营销组合模型中体现为一种变量转换。

 可以使用多种函数对因变量对媒体变量的非线性响应进行建模。例如，我们可以使用简单的对数变换（取广告单位 log(x) 的对数）或幂变换 (x^alpha)。在幂变换的情况下，建模者测试不同变量（参数 x 的不同级别）以获取模型中变量的最高显着性和方程整体的最高显着性。但是，最常见的方法是使用灵活的 S 曲线变换：

参数的变化为建模者提供了对 S 曲线外观的充分灵活性，特别是形状和拐点：

这是收益递减代码中的函数（Hill 函数）：

## step 3: s-curve transformation
gammaTrans <- round(quantile(seq(range(x_normalized)[1], range(x_normalized)[2], length.out = 100), gamma),4)
x_scurve <-  x_normalized**alpha / (x_normalized**alpha + gammaTrans**alpha)

2.3 Facebook Prophet - 趋势、季节性和假期影响

Prophet已包含在代码中，以便通过将数据分解为趋势、季节性和假期组件来改进拟合和预测时间序列。Prophet是 Facebook 的原创程序，它基于一个模型来预测时间序列数据，其中非线性趋势与每年、每周和每天的季节性以及假日效应相吻合。它最适用于具有强烈季节性影响和多个季节历史数据的时间序列。可以在此处找到更多详细信息。

2.4 自动超参数选择和优化

MMM 可能包含高基数参数。IE。收益递减 (Hill) 函数的 alphas 和 gammas，以及几何广告库存转换的 thetas。此外，参数维度随着要测量的营销渠道总数成比例增加。因此，非常有必要处理高维参数空间，其中参数数量越多，模型复杂度、维数和计算要求就越大。

为了在优化整体模型精度的同时实现计算效率，我们利用了Facebook 的 Nevergrad 无梯度优化平台。Nevergrad 允许我们通过ask和tell命令优化探索和利用平衡，以执行多目标优化，平衡归一化均方根误差 ( NRMSE ) 和decomp.RSSD比率（支出份额和渠道之间的关系）系数分解份额）提供一组帕累托最优模型解

请在下面找到帕累托模型解决方案的通用图表示例。图表中的每个点代表一个探索的模型解决方案，而左下角的前三行代表最佳模型解决方案。

进化算法的前提是自然选择。在 EA 中，您可能有一组迭代，其中模型将探索的某些系数组合将继续存在并增殖，而不合适的模型将消失并且不会对后代的基因库做出贡献，就像在自然选择中一样。在 robyn 中，我们建议至少进行 500 次迭代，其中每一次迭代都会为其下一代提供反馈，从而引导模型朝着 alphas、gammas 和 thetas 的最佳系数值发展。我们还建议至少进行 40 次试验，这些试验是一组独立的模型初始化，每个试验都具有您在“set_iter”对象下设置的迭代次数。例如，set_iter 上的 500 次迭代 x 40 次试验 = 20000 次不同的迭代和可能的模型解决方案。

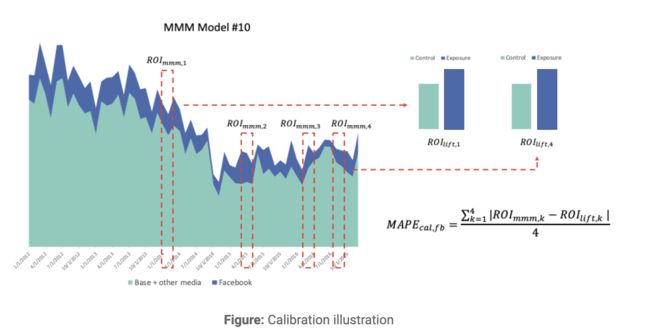
2.5 使用实验结果校准

校准概念#
通过应用随机对照实验的结果，您可以显着提高营销组合模型的准确性。建议定期运行这些，以保持模型永久校准。通常，我们希望将实验结果与营销渠道的 MMM 估计进行比较。从概念上讲，这种方法类似于贝叶斯方法，其中我们使用实验结果作为先验来缩小媒体变量的系数。这些类型的实验的一个很好的例子是 Facebook 的转化提升工具，它可以帮助引导模型朝着特定范围的增量值发展。

 该图说明了一个 MMM 候选模型的校准过程。 Facebook 的 Nevergrad 无梯度优化平台允许我们将MAPE(cal,fb)作为除归一化均方根误差 ( NRMSE ) 和decomp.RSSD比率之外的第三个优化分数（有关更多详细信息，请参阅自动超参数选择和优化） ) 提供一组帕累托最优模型解决方案，最小化并收敛到一组帕累托最优模型候选者。这种校准方法可以应用于其他运行实验的媒体通道，校准的通道越多，MMM模型就越准确。

代码中的校准#
您会发现一个名为“activate_calibration”的变量被定义为 T（真）或 F（假）。如果您想应用校准，请将其设置为 T（真）。因此，您必须添加真实数据，例如来自 Facebook 的转化提升数据、地理测试或多点触控归因。此外，您需要定义要为哪些通道定义某些增量值，以及研究的开始日期、结束日期和增量绝对值 (liftAbs)。在下面的示例中，有两个带有日期的 facebook 研究：从 2018-05-01 到 2018-06-10 和从 2018-07-01 到 2018-07-20。以及 2017 年 11 月 27 日至 2017 年 12 月 3 日的电视地理研究。第一个 Facebook 研究的响应变量（销售额）的绝对值总共提升了 400,000 美元，电视研究的 300,000 美元和 200 美元，

activate_calibration <- F # Switch to TRUE to calibrate model.
# set_lift <- data.table(channel = c("facebook_I",  "tv_S", "facebook_I"),
#                        liftStartDate = as.Date(c("2018-05-01", "2017-11-27", "2018-07-01")),
#                        liftEndDate = as.Date(c("2018-06-10", "2017-12-03", "2018-07-20")),
#                        liftAbs = c(400000, 300000, 200000))

 2.6 输出和分析

MMM 代码将在您在“model_output_collect”对象上指定的文件夹下自动生成一组图。作为“自动超参数选择和优化”部分中提到的多目标优化帕累托优化过程的结果，这些图中的每一个都代表了一个最优模型解决方案。请在下面找到模型输出的示例：

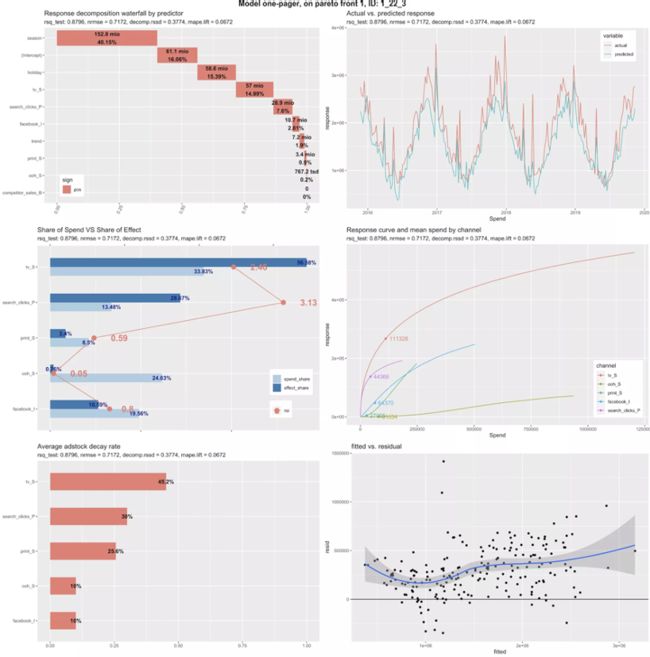
如您所见，上面有 6 个不同的图表：

1 4

2 5

3 6

1. 按预测变量的影响分解瀑布图：这个图表反映了每个变量对响应变量影响的百分比(基线和媒体变量 + 截距)。例如:。如果季节效应说它是40.5% ，这意味着总销售额的40.5% 可以归因于季节性。
2. 支出份额与效果份额：该图反映了通过将各通道的系数分解为响应变量除以总效应得到的总效应的比较。同时，每个渠道的总支出(成本或投资)及其在总营销支出中的相对份额。我们还绘制了投资回报率(ROI)的每个渠道，可以给你一个想法在最有利可图的渠道。
3. 平均广告材料衰减率：这个图表平均代表了每个通道的衰减百分比。衰减率越高，特定通道媒体曝光的时间效应就越长。
4. 实际响应与预测响应：此图显示了响应变量（如销售额）的实际数据，以及该响应变量的建模预测数据如何捕捉实际曲线。我们的目标是建立能够从实际数据中捕获大部分方差的模型，因此，当NRMSE较低时，R平方更接近1。
5. 响应曲线和渠道平均支出：这些是希尔函数的收益递减响应曲线。它们代表渠道的饱和程度，因此可能会建议潜在的预算重新分配策略。曲线到达拐点和水平/平坦斜率的速度越快，每花费额外的 ($) 就会越快饱和。
6. 拟合与残差：此图表显示拟合值和残差值之间的关系。残差值是衡量回归线垂直错过数据点的程度。残差图通常用于发现回归问题。一些数据集不是回归的良好候选者，例如离线的距离变化很大的点。如果残差图中的点随机分布在水平轴周围，则适合该数据的线性回归模型；否则，非线性模型更合适。

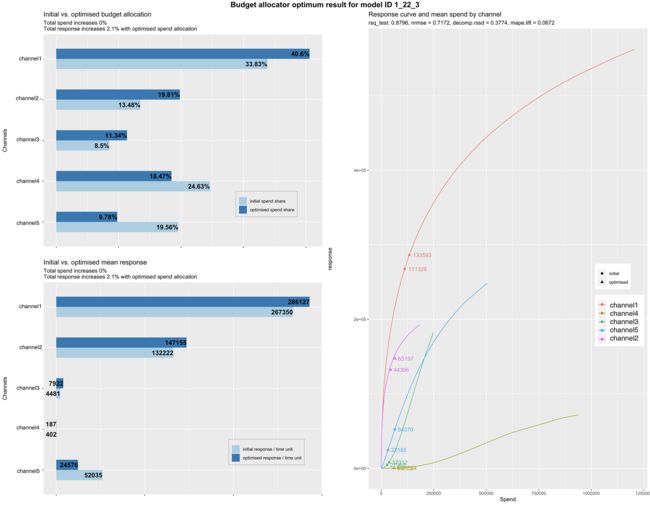
一旦您分析了最佳模型结果图并选择了您的模型，您就可以从上一节的结果中引入模型唯一 ID。例如，设置 modID = "1_22_3" 可以是从“model_output_collect$allSolutions”结果对象中的最佳模型列表中选择的模型的示例。运行预算分配器后，结果将被绘制并保存在保存模型图的同一文件夹下。结果如下所示：

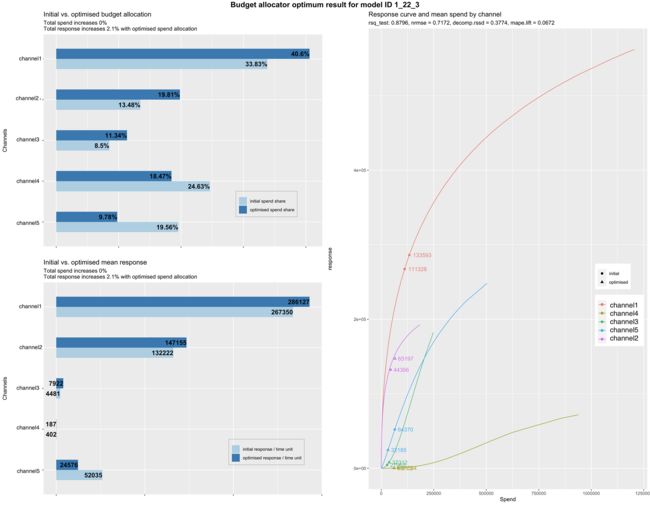
您可能会遇到如上例所示的三个图表：

1. 初始预算分配与优化预算分配：此渠道显示原始支出份额与新的优化推荐支出份额。如果优化份额大于原始份额，则意味着您需要根据两个份额之间的差异按比例增加该渠道的预算。如果支出份额大于优化份额，您将减少预算。
2. 初始与优化平均响应：与上图类似，我们有初始和优化份额，但这次超过了总预期响应，例如销售额。优化响应是如果您按照我们上面解释的图表切换预算，增加那些具有更好份额的优化支出并减少那些优化支出低于初始支出的支出，那么我们期望您获得的总销售额增长。
3. 响应曲线和渠道平均支出：这些也是希尔函数的收益递减响应曲线。它们代表渠道的饱和程度，因此可能会建议潜在的预算重新分配策略。曲线到达拐点和水平/平坦斜率的速度越快，每花费额外的 ($) 就会越快饱和。初始平均支出用圆圈表示，优化后的支出用三角形表示。

2 常见问题及注意事项

2.1 常见问题

1 在“model_output_collect”对象上指定的文件夹下自动生成一组图，输出结果在哪？

        在fb_robyn.exec.R文件目录下，以“日期和时间”作为文件夹保存结果。eg:2021-09-18 10.51

2 f.inputWrangling报错

        1. 时间格式的错误：

        数据集中的 DATE 列必须采用“yyyy-mm-dd”格式。如“2020-01-01”

        2. 中文语言系统，使用week为单位的时序数据，需要更改源文件fb_robyn.func.R：

        463行更改为中文的星期一和星期天

        weekStartMonday <- if(weekStartInput=="星期一") {TRUE} else if (weekStartInput=="星期天")

        3. 确保变量名及格式都正确定义的情况下：

        检查dt_input取得的数据源是CSV文件获取的，excel文件会报错

        4. set_mediaSpendName和set_mediaVarName不能有含空格符命名渠道：

        参数区间定义的命名必然是xxx_alphas或xxx_gammas或xxx_thetas，所有空格必须用下划线替换

        5. prophet的错误，不需要指定地域但是仍然报错：

        检查set_country是否正确，是否在dt_holidays的country中含有对应的地域，并且地域只能输入一个。除非不用prophet功能（即activate_prophet为F），可以不设定set_country。

2.2 注意事项

1 首次运行，请按照1.4.2的操作配置好环境

2 首次运行，到92行，查看并确认CPU核心数

registerDoSEQ(); detectCores()

在电脑空闲（无其他大型程序执行），set_cores设定为 CPU核心数-2或者-1

3 每次做出的output_collect不一定是同样的个数及结果。这个过程无法复现。

4 输出后的结果保存在文件夹内，包含的文件有：

数字组成的png文件：代表不同参数组合出的模型拟合分析结果

hypersampling.png：各模型的alphas/gammas/thetas最后收敛时落在区间的位置。由于Nevergrad的搜索是无梯度下降方法，最终存在局部最小

pareto_front.png：由Nevergrad的ask和tell命令优化探索和平衡，进行多目标优化。得到各模型根据归一化均方根误差（NRMSE）和decomp.RSSD的比率（支出份额和渠道系数分解份额之间的关系）提供一组帕累托最优模型解决方案

spend_exposure_fitting.png：在使用渠道的曝光量（点击率等）与对应渠道的支出，会建立线性和非线性关系（Michaelis-Menten酶促反应公式，注意事项的第5项将会说明这个公式）如果没有曝光量（点击率等）就不会有这个图。

pareto_aggregated.csv：包含每个模型中各渠道的系数，roi，spend，response等信息。是重载当前版本文件夹信息的依据（重载到dt_hyppar_fixed变量中）

pareto_alldecomp_matrix.csv：基于各模型确定下来的alphas/gammas/thetas进行线性拟合，在各时间上各渠道的线性系数。（含prophet处理后的变量）

pareto_hyperparameters.csv：各模型各渠道对应的alphas/gammas/thetas取值

pareto_media_transform_matrix.csv：各模型各渠道经过变换校准（第1节中2.2说明）的数据，并且作为拟合的数据源。

xx_xx_xx_reallocated.csv：在运行 f.budgetAllocator（第199行）才会生成。描述xx_xx_xx这个模型的优化分配数据。

5 Michaelis-Menten酶促反应公式（不理解可以跳过）

是一种描述非线性关系的流量相关公式。

原先用于：化学（这个领域不太了解）生物领域。在生物领域上可以用于药代动力学的计算，如抗癌药物的代谢：药物排泄消除的模型，存在有Michaelis-Mente消除过程还有自身一级速率的线性消除过程。图文描述详见非线性药物（抗癌药）的半衰期 部分

迁移到曝光~支出关系上：也可以认为是一种仓室模型的代谢流动模型。仓室浓度->渠道支出；仓室反应速率->曝光量≈支出速率

6 pareto_aggregated.csv：

coef：各渠道在广义线性拟合的系数

xDecompAgg：各渠道的spend’*coef在时间上的求总和

xDecompPerc：xDecompAgg的归一化：xDecompAgg/sum(y_hat) 【y_hat 单个时间点<- rowSums(xDecomp)】

xDecompMeanNon0：各渠道的xDecomp在全部时间上的平均值 mean(xDecomp)

xDecompMeanNon0Perc：xDecompMeanNon0的归一化：xDecompMeanNon0/sum(xDecompMeanNon0) 均时各chn/均时总chn

xDecompOutAggMeanNon0coefy：各渠道的xDecomp在全部时间上的总和 sum(xDecomp)

pos：是否对于收入是正向的影响？

mape：在使用activate_calibration后，与校准前的差距。详见第一部分的2.5节。

nrmse：该模型拟合结果的正规化方均根差

decomp.rssd：该模型拟合结果的 平方距离的分解根之和。解释业务逻辑的指标。直觉是这样的：假设你在电视上花费了 90%，在 FB 上花费了 10%。如果你获得 10% 的 TV 效果和 90% 的 FB 效果，您可能不会相信这个结果，无论模型误差 (NRMSE) 有多低。如果你得到 80% 的电视和 20% 的 FB 作为效果份额，它会更“现实”。这就是逻辑的来源：最小化支出份额和效果份额之间的距离。这实际上是为了摆脱非常极端的情况，并获得一组更现实的结果。

adstock.ssisd：衰减的平方和（没什么用）

rsq_train：拟合的R**2

lambda：岭回归选择的lambda数值

iterPar：并行计算的第几次

iterNG：Nevergrad迭代的第几次

trials：初始试验的第几次

robynPareto：在帕累托平面的第几个【共1 2 3】

total_spend：各渠道支出总和

mean_spend：各渠道平均支出

spend_share：花费程度（归一化）mean_spend / sum(mean_spend)

effect_share：有效程度（归一化）xDecompMeanNon0Perc/sum(xDecompMeanNon0Perc)

roi：投资回报率 xDecompMeanNon0/mean_spend

mean_response：coef *  [get_spend_mm**alpha / (get_spend_mm**alpha + gammaTrans**alpha)] 见下图 平均回报

next_unit_response 见下图 边际回报

  7 xx_xx_xx_reallocated.csv：

histSpend：渠道过去的历史花费

histSpendTotal：历史总渠道花费

initSpendUnitTotal：各渠道平均花费的总和 sum(xDecompAggMedia$mean_spend)

initSpendUnit：各渠道历史平均花费 mean_spend

initSpendShare：各渠道历史花费贡献度 spend_share

initResponseUnit：各渠道历史平均回报 mean_response

initResponseUnitTotal： 历史总渠道回报

initRoiUnit：各渠道历史ROI mean_response/mean_spend

expSpendTotal：历史总渠道总花费之和 sum(xDecompAggMedia$total_spend)

expSpendUnitTotal：历史总渠道平均花费之和 sum(xDecompAggMedia$mean_spend)

expSpendUnitDelta：expSpendUnitTotal/histSpendUnitTotal-1

optmSpendUnit：非线性约束最优解的各渠道花费

optmSpendUnitDelta：(nlsMod$solution / histSpendUnit -1)

optmSpendUnitTotal：非线性约束最优解的各渠道花费总和

optmSpendShareUnit：最优各渠道花费贡献度 nlsMod$solution / sum(nlsMod$solution)

optmResponseUnit：各渠道最优回报 -coeff * sum( (1 + gammaTran**alpha / xAdstocked **alpha)**-1) gammaTran=gamma' xAdstocked=spend' 见上图

optmResponseUnitTotal：各渠道最优回报总和

optmRoiUnit：各渠道最优回报/非线性约束最优解的各渠道花费

optmResponseUnitLift：各渠道最优回报/各渠道历史平均回报-1