时序信号的时域、频域、时-频域特征提取
文章目录
- 时域特征提取
- 频域特征提取
- 时-频域特征提取
- 参考资料
在面对工业中的传感器采集到的高维的信号,如振动信号,通常需要对数据进行统计特征提取,以进行降维。对于这类时序信号,常用的有时域、频域和时-频域特征提取方法。本次对这三个方面的特征提取代码进行一下总结,并以IEEE PHM 2012 挑战赛的轴承数据集中的Bearing 1_1 的数据进行示例。
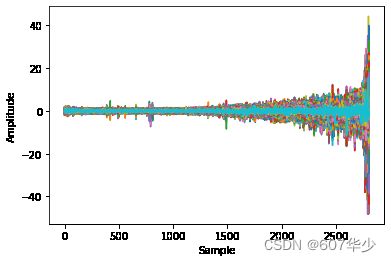
Bearing 1_1的数据维度为(2803, 2560),即共有2803个样本,每个样本数据的信号长度为2560,具体的数据介绍资料比较多,可以自行百度或看直接看官方的数据介绍。
时域特征提取
时域统计特征可分为有量纲统计量和无量纲统计量,有量纲统计量的数值大小会因外界一些物理量的变化而变化,而无量纲统计量不易受外界因素的干扰影响,且通常对早期的微弱故障敏感。
常用的时域统计特征如下:
| 特征 | 公式 | 特征 | 公式 |
|---|---|---|---|
| 最大值 | F 1 = max ( X ( i ) ) F_1=\max \left( X\left( i \right) \right) F1=max(X(i)) | 标准差 | F 9 = ∑ i = 1 N ( X ( i ) − F 4 ) 2 N − 1 F_9=\sqrt{\frac{\sum\nolimits_{i=1}^N{\left( X\left( i \right) -F_4 \right) ^2}}{N-1}} F9=N−1∑i=1N(X(i)−F4)2 |
| 最大绝对值 | F 2 = max ( ∣ X ( i ) ∣ ) F_2=\max \left( \lvert X\left( i \right) \rvert \right) F2=max(∣X(i)∣) | 峭度 | F 10 = ∑ i = 1 N ( X ( i ) − F 4 ) 4 ( N − 1 ) F 9 4 F_{10}=\frac{\sum\nolimits_{i=1}^N{\left( X\left( i \right) -F_4 \right) ^4}}{\left( N-1 \right) {F_9}^4} F10=(N−1)F94∑i=1N(X(i)−F4)4 |
| 最小值 | F 3 = min ( X ( i ) ) F_3=\min \left( X\left( i \right) \right) F3=min(X(i)) | 偏度 | F 11 = ∑ i = 1 N ( X ( i ) − F 4 ) 3 ( N − 1 ) F 9 3 F_{11}=\frac{\sum\nolimits_{i=1}^N{\left( X\left( i \right) -F_4 \right) ^3}}{\left( N-1 \right) {F_9}^3} F11=(N−1)F93∑i=1N(X(i)−F4)3 |
| 均值 | F 4 = 1 N ∑ i = 1 N X ( i ) F_4=\frac{1}{N}\sum\nolimits_{i=1}^N{X\left( i \right)} F4=N1∑i=1NX(i) | 裕度指标 | F 12 = F 2 F 8 F_{12}=\frac{F_2}{F_8} F12=F8F2 |
| 峰峰值 | F 5 = F 1 − F 3 F_5=F_1-F_3 F5=F1−F3 | 波形指标 | F 13 = F 7 F 6 F_{13}=\frac{F_7}{F_6} F13=F6F7 |
| 绝对平均值 | F 6 = 1 N ∑ i = 1 N ∣ X ( i ) ∣ F_6=\frac{1}{N}\sum\nolimits_{i=1}^N{ \lvert X \left( i \right) \rvert } F6=N1∑i=1N∣X(i)∣ | 脉冲指标 | F 14 = F 2 F 6 F_{14}=\frac{F_2}{F_6} F14=F6F2 |
| 均方根值 | F 7 = 1 N ∑ i = 1 N X ( i ) 2 F_7=\sqrt{\frac{1}{N}\sum\nolimits_{i=1}^N{X\left( i \right) ^2}} F7=N1∑i=1NX(i)2 | 峰值指标 | F 15 = F 2 F 7 F_{15}=\frac{F_2}{F_7} F15=F7F2 |
| 方根幅值 | F 8 = ( 1 N ∑ i = 1 N ∣ X ( i ) ∣ ) 2 F_8=(\frac{1}{N}\sum\nolimits_{i=1}^N{\sqrt{ \lvert X \left( i \right) \rvert}})^2 F8=(N1∑i=1N∣X(i)∣)2 |
在设备运行良好的状态下,最大值或最大绝对值(也可以视为峰值)变化范围不大,基本上稳定在一个阈值以下,但一旦最大值或最大绝对值异常变大,基本上可以认为设备健康状况出现了问题,大到一定程度一定是出现了某种故障隐患;
均值反映了在机械运转过程中,由于轴心位置的变化而产生的振动信号的变化;
均方根值,又称有效值反应了振动信号的能量强度和稳定性。工程人员通常最关心的通常就是这个指标,这个指标如果异常变大,则表示机械设备很有可能存在某种隐患;
峭度反应了振动信号的冲击特性,峭度对于冲击比较敏感,一般情况下峭度值应该在3左右,因为正态分布的峭度等于3,如果偏离3太多则说明机械设备存在一定的冲击性振动,可能存在某种故障隐患;
偏度反映了振动信号的非对称性,通常情况下振动信号是关于x轴对称的,这时候偏度应该趋近于0。如果设备某一个方向的摩擦或碰撞较大就会造成振动的不对称,使偏度变大。
裕度指标常用来检测机械设备的磨损状况;
脉冲指标和峰值指标都是用来检测信号中有无冲击的指标。
import numpy as np
from scipy import stats
def get_time_domain_feature(data):
"""
提取 15个 时域特征
@param data: shape 为 (m, n) 的 2D array 数据,其中,m 为样本个数, n 为样本(信号)长度
@return: shape 为 (m, 15) 的 2D array 数据,其中,m 为样本个数。即 每个样本的16个时域特征
"""
rows, cols = data.shape
# 有量纲统计量
max_value = np.amax(data, axis=1) # 最大值
peak_value = np.amax(abs(data), axis=1) # 最大绝对值
min_value = np.amin(data, axis=1) # 最小值
mean = np.mean(data, axis=1) # 均值
p_p_value = max_value - min_value # 峰峰值
abs_mean = np.mean(abs(data), axis=1) # 绝对平均值
rms = np.sqrt(np.sum(data**2, axis=1) / cols) # 均方根值
square_root_amplitude = (np.sum(np.sqrt(abs(data)), axis=1) / cols) ** 2 # 方根幅值
# variance = np.var(data, axis=1) # 方差
std = np.std(data, axis=1) # 标准差
kurtosis = stats.kurtosis(data, axis=1) # 峭度
skewness = stats.skew(data, axis=1) # 偏度
# mean_amplitude = np.sum(np.abs(data), axis=1) / cols # 平均幅值 == 绝对平均值
# 无量纲统计量
clearance_factor = peak_value / square_root_amplitude # 裕度指标
shape_factor = rms / abs_mean # 波形指标
impulse_factor = peak_value / abs_mean # 脉冲指标
crest_factor = peak_value / rms # 峰值指标
# kurtosis_factor = kurtosis / (rms**4) # 峭度指标
features = [max_value, peak_value, min_value, mean, p_p_value, abs_mean, rms, square_root_amplitude,
std, kurtosis, skewness,clearance_factor, shape_factor, impulse_factor, crest_factor]
return np.array(features).T
频域特征提取
除了在时域进行特征分析外,我们通常还会再频域对信号进行分析。通过傅里叶变换将时域信号转变为频谱,即可在频域中对信号进行分析。
常用的频域特征有:
| 特征 | 公式 | 特征 | 公式 |
|---|---|---|---|
| 重心频率 | F 1 = ∑ k = 1 K f k S ( k ) ∑ k = 1 K S ( k ) F_{1}=\frac{\sum\nolimits_{k=1}^K{f_kS\left( k \right)}}{\sum\nolimits_{k=1}^K{S\left( k \right)}} F1=∑k=1KS(k)∑k=1KfkS(k) | 频率均方根 | F 3 = ∑ k = 1 K f k 2 S ( k ) ∑ k = 1 K S ( k ) F_{3}=\sqrt{\frac{\sum\nolimits_{k=1}^K{{f_k}^2S\left( k \right)}}{\sum\nolimits_{k=1}^K{S\left( k \right)}}} F3=∑k=1KS(k)∑k=1Kfk2S(k) |
| 平均频率 | F 2 = ∑ k = 1 K S ( k ) K F_{2}=\frac{\sum\nolimits_{k=1}^K{S\left( k \right)}}{K} F2=K∑k=1KS(k) | 频率方差 | F 4 = ∑ k = 1 K ( f k − F 1 ) 2 S ( k ) ∑ k = 1 K S ( k ) F_{4}=\frac{\sum\nolimits_{k=1}^K{\left( f_k-F_{1} \right) ^2S\left( k \right)}}{\sum\nolimits_{k=1}^K{S\left( k \right)}} F4=∑k=1KS(k)∑k=1K(fk−F1)2S(k) |
import numpy as np
def get_frequency_domain_feature(data, sampling_frequency):
"""
提取 4个 频域特征
@param data: shape 为 (m, n) 的 2D array 数据,其中,m 为样本个数, n 为样本(信号)长度
@param sampling_frequency: 采样频率
@return: shape 为 (m, 4) 的 2D array 数据,其中,m 为样本个数。即 每个样本的4个频域特征
"""
data_fft = np.fft.fft(data, axis=1)
m, N = data_fft.shape # 样本个数 和 信号长度
# 傅里叶变换是对称的,只需取前半部分数据,否则由于 频率序列 是 正负对称的,会导致计算 重心频率求和 等时正负抵消
mag = np.abs(data_fft)[: , : N // 2] # 信号幅值
freq = np.fft.fftfreq(N, 1 / sampling_frequency)[: N // 2]
# mag = np.abs(data_fft)[: , N // 2: ] # 信号幅值
# freq = np.fft.fftfreq(N, 1 / sampling_frequency)[N // 2: ]
ps = mag ** 2 / N # 功率谱
fc = np.sum(freq * ps, axis=1) / np.sum(ps, axis=1) # 重心频率
mf = np.mean(ps, axis=1) # 平均频率
rmsf = np.sqrt(np.sum(ps * np.square(freq), axis=1) / np.sum(ps, axis=1)) # 均方根频率
freq_tile = np.tile(freq.reshape(1, -1), (m, 1)) # 复制 m 行
fc_tile = np.tile(fc.reshape(-1, 1), (1, freq_tile.shape[1])) # 复制 列,与 freq_tile 的列数对应
vf = np.sum(np.square(freq_tile - fc_tile) * ps, axis=1) / np.sum(ps, axis=1) # 频率方差
features = [fc, mf, rmsf, vf]
return np.array(features).T
时-频域特征提取
为了全面的分析信号,除了单一的在时域、频域进行信号分析,我们还会综合在时-频域进行信号分析。常用的时-频域信号分析有小波包分析和EMD信号分析等,这里主要使用小波包信号分析。
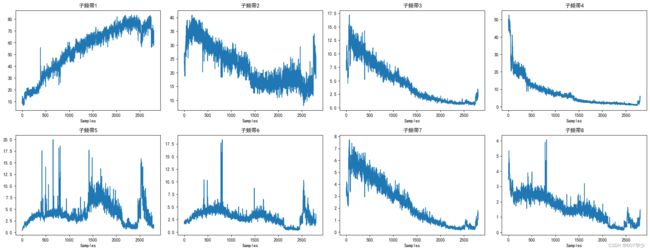
在小波包的信号分析中,我们通常会以 最后一层 子频带 的 能量百分比 作为所提取到时-频域特征。
import pywt
import numpy as np
def get_wavelet_packet_feature(data, wavelet='db3', mode='symmetric', maxlevel=3):
"""
提取 小波包特征
@param data: shape 为 (n, ) 的 1D array 数据,其中,n 为样本(信号)长度
@return: 最后一层 子频带 的 能量百分比
"""
wp = pywt.WaveletPacket(data, wavelet=wavelet, mode=mode, maxlevel=maxlevel)
nodes = [node.path for node in wp.get_level(maxlevel, 'natural')] # 获得最后一层的节点路径
e_i_list = [] # 节点能量
for node in nodes:
e_i = np.linalg.norm(wp[node].data, ord=None) ** 2 # 求 2范数,再开平方,得到 频段的能量(能量=信号的平方和)
e_i_list.append(e_i)
# 以 频段 能量 作为特征向量
# features = e_i_list
# 以 能量百分比 作为特征向量,能量值有时算出来会比较大,因而通过计算能量百分比将其进行缩放至 0~100 之间
e_total = np.sum(e_i_list) # 总能量
features = []
for e_i in e_i_list:
features.append(e_i / e_total * 100) # 能量百分比
return np.array(features)
Bearing1_1的时-频域特征提取示例:
在进行小波包变换时,由于
pywt.WaveletPacket函数只能接收一维数据,因此不能直接将二维矩阵传入函数,需要通过循环处理:# 按照上诉的示例,假设需要处理的数据变量名为 data,其维度为 (2803, 2560) time_frequency_doamin_frequency = [] # 通过for循环每次提取一个样本的时-频域特征 for i in range(data.shape[0]): wavelet_packet_feature = get_wavelet_packet_feature(data[i]) time_frequency_doamin_frequency.append(wavelet_packet_feature) time_frequency_doamin_frequency = np.array(time_frequency_doamin_frequency) time_frequency_doamin_frequency.shape # (2803, 8)
参考资料
[1]. 机械振动信号中的常用指标 (baidu.com)
[2]. 信号时域分析方法的理解(峰值因子、脉冲因子、裕度因子、峭度因子、波形因子和偏度等) - 知乎 (zhihu.com)
[3]. FFT与频谱、功率谱、能量谱等 - SYAO
[4]. 频域特征指标及其MATLAB代码实现(重心频率、均方频率、均方根频率、频率方差、频率标准差) - 知乎 (zhihu.com)
[5]. 雷亚国. 旋转机械智能故障诊断与剩余寿命预测[M]. 西安: 西安交通大学出版社, 2017.