机器学习示例总结（线性回归、逻辑回归、KNN算法、朴素贝叶斯、SVM算法、决策树）

 以下所有内容均为在华为云学习的总结

AI技术领域课程--机器学习_在线课程_华为云开发者学堂_云计算培训-华为云 (huaweicloud.com)

目录

 线性回归

逻辑回归算法实现

逻辑回归介绍

KNN算法

KNN算法实现

朴素贝叶斯介绍

朴素贝叶斯算法实现

SVM支持向量机

 SVM算法实现

决策树

---

线性回归

# 导入sklearn下的LinearRegression 方法
from sklearn.linear_model import LinearRegression
import numpy as np
model = LinearRegression()

# 构造用于训练的数据集
x_train = np.array([[2,4],[5,8],[5,9],[7,10],[9,12]])
y_train = np.array([20,50,30,70,60])

# 训练模型并输出模型系数和训练结果
model.fit(x_train,y_train)
#fit(x,y,sample_weight=None)x:训练集 y:目标值 sample_weight:每个样本的个数
#coef_ 系数w,intercept_截距
print(model.coef_) #输出系数w
print(model.intercept_) #输出截距b
print(model.score(x_train,y_train)) #输出模型的评估分数R2

逻辑回归算法实现

逻辑回归介绍

logistic回归又称logistic回归分析，是一种广义的线性回归分析模型，常用于数据挖掘，疾病自动诊断，经济预测等领域。例如，探讨引发疾病的危险因素，并根据危险因素预测疾病发生的概率等。以胃癌病情分析为例，选择两组人群，一组是胃癌组，一组是非胃癌组，两组人群必定具有不同的体征与生活方式等。因此因变量就为是否胃癌，值为“是”或“否”，自变量就可以包括很多了，如年龄、性别、饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的，也可以是分类的。然后通过logistic回归分析，可以得到自变量的权重，从而可以大致了解到底哪些因素是胃癌的危险因素。同时根据该权值可以根据危险因素预测一个人患癌症的可能性。

其中MoXing是华为云深度学习服务提供的网络模型开发API。相对于TensorFlow和MXNet等原生API而言，MoXing API让模型的代码编写更加简单，而且能够自动获取高性能的分布式执行能力。

import numpy as np
#从sklearn导入LogisticRegression方法
from sklearn.linear_model import LogisticRegression
#导入划分训练集和测试集的方法
from sklearn.model_selection import train_test_split

X = np.random.randint(2, size=(6, 100))
Y = np.array([1, 2, 3, 4, 4, 5])


#划分训练集及测试集
#划分训练集和测试集，测试集占数据集的30%，训练集占数据集的70%
train_x,test_x,train_y,test_y=train_test_split(X,Y,test_size=0.3)
#train_test_split(x,y,test_size=0.3)     #参数test_size测试集占比; x:数据集; y:数据集的目标值
model = LogisticRegression()#调用sklearn里面的方法
model.fit(train_x,train_y)#通过训练集得到训练后的模型
#测试模型
pred_y=model.predict(test_x)
# 输出判断预测是否与真实值相等
print(pred_y==test_y)
print(model.score(test_x,test_y))

KNN算法

KNN是通过测量不同特征值之间的距离进行分类。它的思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别，其中K通常是不大于20的整数。KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

KNN算法实现

#从sklearn 导入KNeighborsClassifier方法
from sklearn.neighbors import KNeighborsClassifier
import numpy as np

#；提供简单的数据结构进行后续的KNN算法验证
X = np.array([[1,1],[1,1.5],[2,2.5],[2.5,3],[1.5,1],[3,2.5]])
y = ['A','A','B','B','A','B']

#调用KNN算法
model = KNeighborsClassifier(n_neighbors=4, algorithm='ball_tree')

model.fit(X, y)

#预测
print(model.predict([[1.75,1.75]])) #输出分类结果
print(model.predict_proba([[1.75,1.75]])) #返回预测属于某标签的概率
print(model.score(X,y)) #输出模型训练结果

朴素贝叶斯介绍

朴素贝叶斯分类器是一系列以假设特征之间强（朴素）独立下运用贝叶斯定理为基础的简单概率分类器。该分类器模型会给问题实例分配用特征值表示的类标签，类标签取自有限集合。它不是训练这种分类器的单一算法，而是一系列基于相同原理的算法：所有朴素贝叶斯分类器都假定样本每个特征与其他特征都不相关。

朴素贝叶斯算法实现

import numpy as np
from sklearn.naive_bayes import BernoulliNB

X = np.random.randint(2, size=(6, 100))
Y = np.array([1, 2, 3, 4, 4, 5])

clf = BernoulliNB()
clf.fit(X, Y)

print(clf.predict(X[2:3]))

SVM支持向量机

支持向量机（Support Vector Machine, SVM）是一类按监督学习方式对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面。

 SVM算法的优缺点：

优点：

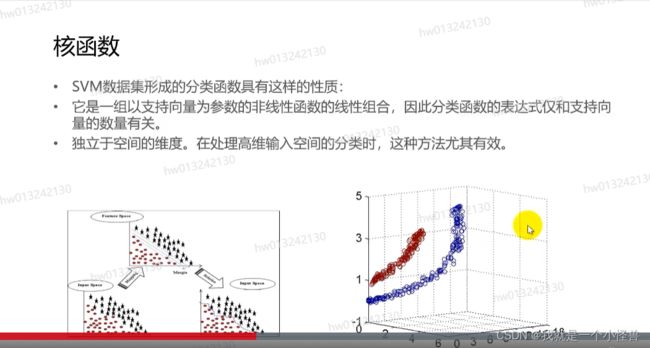
1.使用核函数可以向高维空间进行映射

2.使用核函数可以解决非线性的分类

3.分类思想很简单，就是将样本与决策面的间隔最大化

4.分类效果较好

缺点：

1.SVM算法对大规模训练样本难以实施

2.用SVM解决多分类问题存在困难

3.对缺失数据敏感，对参数和核函数的选择敏感

 SVM算法实现

import matplotlib.pyplot as plt
import numpy as np
import moxing as mox
from sklearn import svm

#X，Y为准备好的数据
clf = svm.SVC(C=5,kernel='linear',gamma=10)
clf.fit(X, Y)


# 获取分割超平面
w = clf.coef_[0]
# 斜率
a = -w[0] / w[1]
# 从-2到10，顺序间隔采样50个样本，默认是num=50
xx = np.linspace(-2, 10)  # , num=50)
# 二维的直线方程
yy = a * xx - (clf.intercept_[0]) / w[1]
print("yy=", yy)

#通过支持向量绘制分割超平面
print("support_vectors_=", clf.support_vectors_)
b = clf.support_vectors_[0]
yy_down = a * xx + (b[1] - a * b[0])
b = clf.support_vectors_[-1]
yy_up = a * xx + (b[1] - a * b[0])

plt.plot(xx, yy, 'k-')
plt.plot(xx, yy_down, 'k--')
plt.plot(xx, yy_up, 'k--')

plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=80, facecolors='none')
plt.scatter(X[:, 0].flat, X[:, 1].flat, c=Y, cmap=plt.cm.Paired)
plt.axis('tight')
plt.show()

决策树

ID3算法介绍

从信息论的知识可知：信息熵越大，从而样本纯度越低。

ID3 算法的核心思想就是以信息增益来度量特征选择，选择信息增益最大的特征进行分裂。它表示得知特征 A 的信息而使得样本集合不确定性减少的程度，

算法采用自顶向下的贪婪搜索遍历可能的决策树空间（C4.5 也是贪婪搜索）。 其大致步骤为：

• 初始化特征集合和数据集合；

• 计算数据集合信息熵和所有特征的条件熵，选择信息增益最大的特征作为当前决策节点；

• 更新数据集合和特征集合（删除上一步使用的特征，并按照特征值来划分不同分支的数据集合）；

• 重复 2，3 两步，若子集值包含单一特征，则为分支叶子节点。

#此代码非本人所写
from sklearn.model_selection import cross_val_score
from sklearn.datasets import make_blobs
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.tree import DecisionTreeClassifier
 
##创建100个类共10000个样本，每个样本10个特征
X, y = make_blobs(n_samples=10000, n_features=10, centers=100,random_state=0)
 
## 决策树
clf1 = DecisionTreeClassifier(max_depth=None, min_samples_split=2,random_state=0)
scores1 = cross_val_score(clf1, X, y)
print(scores1.mean())
 
 
## ExtraTree极限树分类器集合
clf3 = ExtraTreesClassifier(n_estimators=10, max_depth=None,min_samples_split=2, random_state=0)
scores3 = cross_val_score(clf3, X, y)
print(scores3.mean())