机器学习笔记

目录

 

常用基本库

第零部分 数据勘察

1、去除重复值

2、查看数据分布

第一部分 数据预处理

1、数据清洗

2、数据变换

第二部分：特征选择

方差过滤特征

相关性过滤特征

Embedded嵌入法 

降维筛选

第三部分：数据集拆分

第四部分：数据挖掘模型

1、线性回归 

2、逻辑回归LR

3、朴素贝叶斯 NB

4、支持向量机SVM 

5、最近邻分类 KNN

6、神经网络

9、决策树 DT

10、集成算法

11、网格搜索

12、聚类分析

---

常用基本库

         

                                      

                 

 

第零部分 数据勘察

1、去除重复值

#1、查看数据是否有重复值
data_ord.duplicated().sum() 
data_ord.drop_duplicates(inplace=True) 
data_na.head()

2、查看数据分布

# 描述性统计
data_med.describe()

# 画出各个特征分布图
object_features = list(set(data_na.columns) - set(['ID', 'Purchase or not','lab']))
for feature in object_features:
    print(feature)
    df_train = data_na[data_na['lab']=='train'].copy()
    
    #如果特征类别数大于 10 个则需要分开做操作
    #to_numeric 把特征值转化为数字类型、unique 去重函数、cut 将数据进行分割 
    
    if feature not in ['User area', 'gender']:
        df_train[feature] = pd.to_numeric(df_train[feature])
    
    if len(df_train[feature].unique())>=20:
        df_train['cut'] = pd.cut(df_train[feature],bins=20, include_lowest=True, right=False, precision=0)
        temp_pivot = df_train.pivot_table(index="cut", values='ID', columns='Purchase or not', aggfunc='count', fill_value=0)
    else:
        temp_pivot = df_train.pivot_table(index=feature, values='ID', columns='Purchase or not', aggfunc='count', fill_value=0)
    temp_pivot['percent'] = temp_pivot[1] / (temp_pivot[0]+temp_pivot[1])
    temp_pivot['percent'].plot.bar()
    plt.show()

第一部分 数据预处理

1、数据清洗

缺失值填补

方法一：
from sklearn.impute import SimpleImputer

imp_mean = SimpleImputer() #实例化，默认均值填补
imp_median = SimpleImputer(strategy="median") #⽤中位数填补
imp_0 = SimpleImputer(strategy="constant",fill_value=0) #⽤0填补

#fit_transform⼀步完成调取结果
data['age'] = imp_mean.fit_transform(Age) 

#使⽤众数填补Embarked
Embarked = data.loc[:,"Embarked"].values.reshape(-1,1)
imp_mode = SimpleImputer(strategy = "most_frequent")
data.loc[:,"Embarked"] = imp_mode.fit_transform(Embarked)

方法二：
data.loc[:,"Age"] = data.loc[:,"Age"].fillna(data.loc[:,"Age"].median())
#.fillna 在DataFrame⾥⾯直接进⾏填补
data.dropna(axis=0,inplace=True)
#.dropna(axis=0)删除所有有缺失值的⾏， .dropna(axis=1)删除所有有缺失值的列
#参数inplace，为True表示在原数据集上进⾏修改，为False表示⽣成⼀个复制对象，不修改原数据

方法三：
# 用 KNN 插入填补离散型特征的缺失值 
from missingpy import KNNImputer
imputer = KNNImputer(n_neighbors=2, weights="uniform")
data_imp=imputer.fit_transform(data_na_imp)

# 用随机森林填补连续缺失值  ****略微耗时 
from missingpy import MissForest 
mf_imp=MissForest() 
data_imp=mf_imp.fit_transform(data_na_imp)

噪声清除
识别噪声的方法：

• 通过排序 观察到过大过小的值
• 在平均值 ±3 倍标准差外的为噪声
• 通过四分位发识别噪声 IQR=Q3=Q1 Q1-1.5IQR ~ Q3+1.5IQR

处理方法：将离群值视为空、天花板/盖帽法、函数矫正 (用log(离群值)/1og10 处理 压缩数据)

# 离群值用分位数进行处理 
per_columns=set(data_imp_result.columns)- set(['ID', 'User area','gender','Purchase or not','lab'])

def cap(x, quantile=[0.05, 0.95]):
    Q05, Q95=x.quantile(quantile).values.tolist()
   
    # 替换异常值为指定的分位数
    if Q05 > x.min():
        x = x.copy()
        x.loc[xQ95] = Q95
    return(x)

# 对训练集进行盖帽法
data_med_2 = data_imp_result[per_columns].apply(cap) 
# 将原始 ID 和 y 列拼接
# new_data = pd.concat([data_imp_result[['ID', 'User area','gender','Purchase or not','lab']], data_med_2], axis=1)

data_result=data_imp_result.copy()
data_result[data_med_2.columns]=data_med_2
data_result.head() 

2、数据变换

数据规范化：属性数据可以缩放 使得他们落在较小的区间

最大最小正规化

#归一化 
from sklearn import preprocessing
mms=preprocessing.MinMaxScaler().fit(df_train.iloc[:,1:-1])
mms.transform(df_train.iloc[:,1:-1]) 
np.around(mms.transform(df_test.iloc[:,1:-1]),2) 

Z 分数正规化

#标准化
from sklearn import preprocessing  
scaler=preprocessing.StandardScaler().fit(df_train.iloc[:,1:-1])
scaler.transform(df_train.iloc[:,1:-1])
np.around(scaler.transform(df_test.iloc[:,1:-1]),2)

数据离散化：通过把值映射到区间或者概念标号变换数值数据 包括 分箱、聚类、决策树、相关分析

# 人工离散 
age_range = list(range(0,111,10))
train_data5['age_cut1'] = pd.cut(train_data5['age'], age_range, include_lowest=True, right=False)
train_data5['age_cut1'].value_counts().sort_index()

# 等宽装箱
train_data5['age_cut2'] = pd.cut(train_data5['age'], bins=10, include_lowest=True, right=False, precision=0)
train_data5['age_cut2'].value_counts().sort_index()

# 等深装箱
train_data5['age_cut3'] = pd.qcut(train_data5['age'], 10, precision=1)
train_data5['age_cut3'].value_counts().sort_index()

概念分层：可以基于模式定义以及每个属性的不同值个数产生  

#分类型特征 编码 3种： 
#自动离散编码 
d = data['Sex'].value_counts()
data['Sex'].replace(pd.Series(range(len(d)), index = d.index))

#LabelEncoder 连续性指派，分类标签转化成分类数值
from sklearn import preprocessing 
code_age=train['age']
lcode=preprocessing.LabelEncoder()
train['age']=lcode.fit_transform(code_age)

# OneHotEncoder 独热编码 创建出哑变量，OrdinalEncoder 有顺序的独热编码
from matplotlib import pyplot as plt 
plt.hist(new_train_data['age'])
new_train_data['SeriousDlqin2yrs'].value_counts()
data=[['female','18','student'],['male','35','engineer'],['female','25','teacher']]

encoder=preprocessing.OneHotEncoder().fit(data)
encoder.transform(data).toarray()
encoder.categories_ ,encoder.get_feature_names() 

#连续型特征 二值化
from sklearn.preprocessing import Binarizer
X = data_2.iloc[:,0].values.reshape(-1,1) #类为特征专⽤，所以不能使⽤⼀维数
组
transformer = Binarizer(threshold=30).fit_transform(X)
transformer

#连续型特征 分段为多分类
from sklearn.preprocessing import KBinsDiscretizer
X = data.iloc[:,0].values.reshape(-1,1)
est = KBinsDiscretizer(n_bins=3, encode='ordinal', strategy='uniform')
est.fit_transform(X)#查看转换后分的箱：变成了⼀列中的三箱
set(est.fit_transform(X).ravel())
est = KBinsDiscretizer(n_bins=3, encode='onehot', strategy='uniform')
#查看转换后分的箱：变成了哑变量
est.fit_transform(X).toarray()
est = KBinsDiscretizer(n_bins=3, encode='onehot', strategy='quantile')
#查看转换后分的箱：变成了哑变量,且每个类别数量基本相等
est.fit_transform(X).toarray().sum(0)

? 数据归约：减少需要考虑的维的个数，将原数据较小表示

维归约：主成分分析

数量归约：等深分箱 等宽分箱 ，抽样

 

第二部分：特征选择

数据过滤：冗余和相关分析；方差过滤，删除方差为 0 没有意义的特征；相关性过滤特征：选出与标签有关且有意义的特征；降维：主成分、因子分析 

方差过滤特征

#优先删掉方差为 0 的特征 0表示所有数据都一样或者数据波动不大 对目标变量就没什么用
from sklearn.feature_selection import VarianceThreshold
X_fs0 = VairanceThreshold().fit_transform(X) #默认方差为 0

#参数threshold表示方差的阈值
VTS=VarianceThreshold(np.median(X.var().values)).fit(X) #实例化并训练模型
X_fsvar =VTS.transform(X)  

#查看模型相关接⼝
VTS.get_support(indices=False) #返回与原特征⻓度相等的布尔索引，被留下的特征为True
VTS.get_support(indices=True) #返回被留下的特征的索引

#提取出所有满⾜要求的特证名,以下两种表达都可以
X.columns[VTS.get_support(indices=False)]
X.columns[VTS.get_support(indices=True)]

#提取出满⾜要求的特征矩阵,以下两种表达都可以
X.iloc[:,VTS.get_support(indices=True)]
X.loc[:,VTS.get_support()]

相关性过滤特征

#特征选取 # filter过滤法 
from sklearn.feature_selection import SelectKBest,chi2,f_classif,mutual_info_classif
#from sklearn.feature_selection import f_regression,mutual_info_regression  
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score 
X=data.iloc[:,1:-1]
Y=data.iloc[:,-1]

# 卡方检验
chi2val, pval = chi2(X, Y)
#k取多少？我们想要消除所有p值⼤于设定值，⽐如0.05或0.01的特征：
k0 = chi2val.shape[0] - (pval > 0.05).sum()
X_fschi = SelectKBest(chi2, k =k0).fit_transform(X, Y)
rfc = RandomForestClassifier(n_estimators = 10)
cross_val_score(rfc, X_fschi, Y, cv = 5).mean()

# F检验
F, pval_f = f_classif(X, Y) 
k1 = F.shape[0] - (pval_f > 0.05).sum()
X_fsf = SelectKBest(f_classif, k = k1).fit_transform(X, Y)
rfc = RandomForestClassifier(n_estimators = 10)
cross_val_score(rfc, X_fsf, Y, cv = 5).mean()

# 互信息法
result = mutual_info_classif(X, Y)
k2 = result.shape[0] - sum(result <= 0)
X_fmif= SelectKBest(mutual_info_classif, k = k2).fit_transform(X, Y)
rfc = RandomForestClassifier(n_estimators = 10)
cross_val_score(rfc, X_fmif, Y, cv = 5).mean()

Embedded嵌入法 

SelectFromModel是⼀个元变换器，可以与任何在拟合后具有coef_， feature_importances_属性或
参数中可选惩罚项的评估器⼀起使⽤（⽐如随机森林和树模型就具有属性feature_importances_，逻辑
回归就带有l1和l2惩罚项，线性⽀持向量机也⽀持l2惩罚项）

from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import RandomForestClassifier as RFC
RFC_ = RFC(n_estimators =10,random_state=0)
X_embedded = SelectFromModel(RFC_,threshold=0.005).fit_transform(X,y)

#画出学习曲线来确定阈值
import numpy as np
import matplotlib.pyplot as plt

RFC_.fit(X,y).feature_importances_
threshold = np.linspace(0,(RFC_.fit(X,y).feature_importances_).max(),20)

score = []
for i in threshold:
  X_embedded = SelectFromModel(RFC_,threshold=i).fit_transform(X,y) 
  once = cross_val_score(RFC_,X_embedded,y,cv=5).mean()
  score.append(once)
plt.plot(threshold,score)
plt.show()

降维筛选

from sklearn.decomposition import PCA

#画累计⽅差贡献率曲线，找最佳降维后维度的范围
pca_line = PCA().fit(X)
plt.figure(figsize=[20,5])
plt.plot(np.cumsum(pca_line.explained_variance_ratio_))
plt.xlabel("number of components after dimension reduction")
plt.ylabel("cumulative explained variance ratio")
plt.show()

#降维后维度的学习曲线，继续缩⼩最佳维度的范围
score = []
for i in range(1,101,10):
X_dr = PCA(i).fit_transform(X)
once = cross_val_score(RFC(n_estimators=10,random_state=0)
,X_dr,y,cv=5).mean()
score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(1,101,10),score)
plt.show()

X_dr = PCA(23).fit_transform(X)
cross_val_score(RFC(n_estimators=100,random_state=0),X_dr,y,cv=5).mean()

#用 pca 降维之后 再用 KNN 算法是否能得到较好的结果
#KNN的k值学习曲线
score = []
for i in range(10):
X_dr = PCA(23).fit_transform(X)
once = cross_val_score(KNN(i+1),X_dr,y,cv=5).mean()
score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(10),score)
plt.show()

第三部分：数据集拆分

from sklearn.mode_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,random_state=50)

 

第四部分：数据挖掘模型

分为 有监督模型和无监督模型

有监督：指有目标字段(比如根据现有的收入值预测明年的收入，根据现有各种类别用户的行为预测其他用户属于哪一种类别)

# 拟合模型
model.fit(X_train, y_train)
# 模型预测
model.predict(X_test)

# 获得这个模型的参数
model.get_params()
# 为模型进行打分
model.score(data_X, data_y) # 线性回归：R square； 分类问题： acc

1、线性回归 

回归模型可以理解为：现有的一个点集，用一条曲线去拟合它分布的过程。如果拟合曲线是一条直线，则称为线性回归。如果是一条二次曲线，则被称为二次回归。
假设函数 用数学的方法描述自变量和因变量之间的关系，它们之间可以是一个线性函数或非线性函数 如 a,b。 
损失函数 用数学的方法衡量假设函数预测结果与真实值之间的误差。差距越小预测越准确，算法的任务就是使差距最小。
在模型训练中优化算法也是至关重要的，它决定了一个模型的精度和运算速度。一般线性回归实例中主要使用梯度下降法进行优化。梯度就是函数变化增长最快的方向 梯度下降就是求函数的最小值 梯度上升就是求函数的最大值

最小损失函数minSSE=∑(Yi-aXi-b) ^2
最小二乘的 SSE 是一个凸函数，凸函数的特点就是只有一个最低点，可以通过求偏导的方法来找到最低点  
SSE 是a,b的函数，因为 a,b未知 
用已知的 x 和 y 的信息去估计一个最好的 a,b 从而使的模型的损失最小
如何找最小值：在此 SSE 中需要先对 b求导 让他等于 0， 得到中间结果后 利用此结果再对 a 求导 让其等于 0 

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error,r2_score

# 定义线性回归模型
model = LinearRegression(fit_intercept=True, normalize=False, 
    copy_X=True, n_jobs=1)
"""
参数
---
    fit_intercept：是否计算截距。False-模型没有截距
    normalize： 当fit_intercept设置为False时，该参数将被忽略。 如果为真，则回归前的回归系数X将通过减去平均值并除以l2-范数而归一化。
     n_jobs：指定线程数
"""
y=ax+b   a:model.coef_   b:model.intercept_

#将预测标签与真实标签一同放入包内 计算均方差 r2得分
mean_squared_error(Y,Y_pred),r2_score(Y,Y_pred)

SST=SSR+SSE ；SST 因变量总变化；SSR因变量可解释变化 ；SSE 因变量不可解释变化；  r2=SSR/SST
线性回归注意事项：
一般要求因变量Y是正态总体的随机变量 
做回归要有实际意义，回归线不可外延
做回归前要绘制散点图，特大特小的离群值需要剔除 
变量之间要排除多重共线性 异方差性 残差自相关性

2、逻辑回归LR

将线性回归所产生的值带入到逻辑方程式，将输出值压制在 0-1 之间，用来预测有一个或者多个自变量构成的分类函数中属于某一类的概率，主要用于因素探索性分析Logistic回归实质：发生概率除以没有发生概率再取对数。就是这个不太繁琐的变换改变了取值区间的矛盾和因变量自变量间的曲线关系。究其原因，是发生和未发生的概率成为了比值 ，这个比值就是一个缓冲，将取值范围扩大，再进行对数变换，整个因变量改变。不仅如此，这种变换往往使得因变量和自变量之间呈线性关系，这是根据大量实践而总结。所以，Logistic回归从根本上解决因变量要不是连续变量怎么办的问题  公式 ：log(p/1-p)=p0+p1x1+.........+pkxk 
如果数据里面没有多重共线性的话，最小二乘（那个最原始的回归）的分数肯定是最好的
如果x里面或多或少出现了多重共线性，我们采用ridge和lasso加上一个恒大于等于0的惩罚项 找到一个局部最优
损失函数 SSE=(y-y_pred).T*(y-y_pred)+ ?
如果损失函数后面是lamabda∑|theta| 表示1范式 Lasso, 用于做特征选取 惩罚强度大 如果损失函数后面是lamabda∑(theta)^2 表示2范式 Ridge 用于数据含有多重共线性

from sklearn.linear_model import LogisticRegression
# 定义逻辑回归模型
model = LogisticRegression(solver='sag',multi_class='multinomial',max_iter=5000)

"""参数
---
    penalty：使用指定正则化项（默认：l2）
    solver:损失函数的优化方法 
    multi_class:'multinomial'
    dual: n_samples > n_features取False（默认）
    C：正则化强度的反，值越小正则化强度越大
    n_jobs: 指定线程数
    random_state：随机数生成器
    fit_intercept: 是否需要常量
"""

优点：
逻辑回归不假设自变量和因变量存在线性关系
逻辑回归不假设因变量和误差变量呈正态分布
预测结果是介于 0-1 之间的概率
可适用于连续型和类别型的自变量
容易使用和解释
缺点：
对模型中自变量多重共线性较为敏感
预测结果呈S型 两端变化小 中间变化大 导致很多区间变量变化对目标概率影响没有区分度 无法确定阈值
逻辑回归相关参数解释 https://blog.csdn.net/laobai1015/article/details/80512849

3、朴素贝叶斯 NB

对于给出的待分类项，求解此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类属于哪个类别。
贝叶斯分类必须限制特征属性必须有条件独立或基本独立 

高斯朴素贝叶斯 ：特征变量是连续变量，符合高斯分布，比如说人的身高，物体的长度。
多项式朴素贝叶斯：特征变量是离散变量，符合多项分布，在文档分类中特征变量体现在一个单词出现的次数，或者是单词的 TF-IDF 值等。
伯努利朴素贝叶斯：特征变量是布尔变量，符合 0/1 分布，在文档分类中特征是单词是否出现。
*伯努利朴素贝叶斯是以文件为粒度，如果该单词在某文件中出现了即为 1，否则为 0。而多项式朴素贝叶斯是以单词为粒度，会计算在某个文件中的具体次数。而高斯朴素贝叶斯适合处理特征变量是连续变量，且符合正态分布（高斯分布）的情况。比如身高、体重这种自然界的现象就比较适合用高斯朴素贝叶斯来处理。而文本分类是使用多项式朴素贝叶斯或者伯努利朴素贝叶斯。

from sklearn import naive_bayes
model = naive_bayes.GaussianNB() # 高斯贝叶斯
model = naive_bayes.MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)
model = naive_bayes.BernoulliNB(alpha=1.0, binarize=0.0, fit_prior=True, class_prior=None)
"""
文本分类问题常用MultinomialNB
参数
---
    alpha：平滑参数
    fit_prior：是否要学习类的先验概率；false-使用统一的先验概率
    class_prior: 是否指定类的先验概率；若指定则不能根据参数调整
    binarize: 二值化的阈值，若为None，则假设输入由二进制向量组成
"""

 

4、支持向量机SVM 

SVM 利用支持向量 SV 作为构建分割超平面的重要数据，最佳的超平面指边界最大化的超平面。(最佳分割线的标准 对之前未见到的数据具有最小分类错误率的直线)，支持向量 SV 即落在最佳跑超平面边缘上的数据，因他们最难分类正确，若他们分类正确了，那么其余的训练数据也都能被正确分类  

优点：
能构建复杂非线性决策边界，通常具有极高准确率
一般不会出现过拟合，因 SVM 不会使用全量数据而是挑选出支持向量
低维空间向量集难以划分，只要选对适当的核函数就能得到高维空间的分类函数(核函数：多项式、高斯、sigmod)
缺点：
训练时间过长        (要计算距离，需要对特征进行规范化)

from sklearn.svm import SVC
model = SVC(C=1.0, kernel=’rbf’, gamma=’auto’)
"""参数
---
    C：误差项的惩罚参数C
    gamma: 核相关系数。浮点数，If gamma is ‘auto’ then 1/n_features will be used instead.
"""

5、最近邻分类 KNN

定义：对于训练集中每条记录 KNN 确定该记录与训练数据集中相似度最近的 K 条记录，根据这些记录数据的类别 将待分类的记录并归到最可能的类别中
KNN 假设：
相同类别的用户有同样的行为
需要判别的点会做跟令居相同的事
优点：
对数据分布没有要求，训练阶段很，可以产生任何形状的决策边界
由于只取前k个最近邻点 对较远的噪声点表现鲁棒，所以能很好的避免样本不平衡
缺点：
不产生模型，发现特征间关系的能力有限
分类阶段很慢，类别变量和缺失值需要额外的处理

from sklearn import neighbors
#定义kNN分类模型
model = neighbors.KNeighborsClassifier(n_neighbors=5, n_jobs=1) # 分类
model = neighbors.KNeighborsRegressor(n_neighbors=5, n_jobs=1) # 回归
"""参数
---
    n_neighbors： 使用邻居的数目
    n_jobs：并行任务数
"""

6、神经网络

定义：类似于大脑神经网络，神经网络中有很多神经元，神经元分为输入层、隐藏层、输出层
输入层：负责接收外界刺激
隐藏层：负责增加计算能力，以解决困难问题
输出层：决策层，负责进行决策 
神经元由上一层神经元与本层神经元交叉形成的神经建、权重加总、常数项、激活函数组成，激活函数是一个以权重加和及常数项之和为自变量的函数
优点：
自学习能力和自适应能力强
用各种非线性连续函数作为激活函数 给模型提供了非线性映射能力，能解决更复杂的问题
容错能力 部分神经元受损 对整体结果不会造成太大影响
缺点：
对初始网络权重非常敏感，以不同的权重初始化网络，其往往会收敛于不同的局部极小 
BP 神经网络算法的收敛速度慢
过拟合问题？

     

 

from sklearn.neural_network import MLPClassifier
# 定义多层感知机分类算法
model = MLPClassifier(activation='relu', solver='adam', alpha=0.0001)
"""参数
---
    hidden_layer_sizes: 元祖
    activation：激活函数
    solver ：优化算法{‘lbfgs’, ‘sgd’, ‘adam’}
    alpha：L2惩罚(正则化项)参数。
"""

9、决策树 DT

在已知各种情况发生的概率下 通过构成决策树来求取净现值的期望值大于等于 0 的小概率 评价项目风险 
决策树生成过程：
将所有训练数据放在根节点
字段选择：根据所选字段将数据进行切割 
决策树修剪：修剪过程就是溢出部分树分支 避免过拟合 提高模型准确度 
字段选择方法有：ID3，C4.5 ，C5.0， CART， CHAID 

                        

from sklearn import tree 
model = tree.DecisionTreeClassifier(criterion=’gini’, max_depth=None, 
    min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, 
    max_features=None, random_state=None, max_leaf_nodes=None, 
    min_impurity_decrease=0.0, min_impurity_split=None,
     class_weight=None, presort=False)
"""参数
---
    criterion ：特征选择准则gini/entropy
    max_depth：树的最大深度，None-尽量下分
    min_samples_split：分裂内部节点，所需要的最小样本树
    min_samples_leaf：叶子节点所需要的最小样本数
    max_features: 寻找最优分割点时的最大特征数
    max_leaf_nodes：优先增长到最大叶子节点数
    min_impurity_decrease：如果这种分离导致杂质的减少大于或等于这个值，则节点将被拆分。
"""

10、集成算法

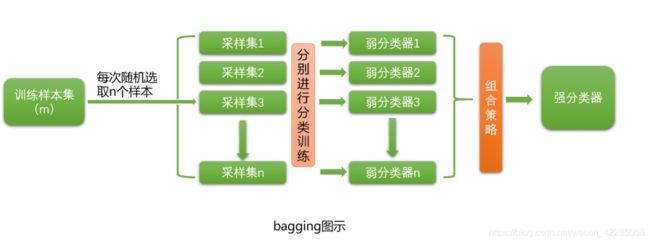
集成算法：将若干个弱分类器通过一定的策略组合之后产生一个强分类器，分 3 类：装袋法(bagging)、提升法(boosting)、堆叠法(stacking)
装袋法(bagging): 根据均有概率分布从数据集中有放回的重复抽样，每个新数据及和原始数据集大小相等
优点：
各个预测函数可以并行生成 节省大量时间开销 
能在一定程度上解决过拟合，但是可能会欠拟合
缺点：单个评估其学习能力较弱的的时候 bagging 无法提升模型表现 
目标：降低方差，提高模型整体的稳定性
代表算法：随机森林

提升法(boosting)：是一个迭代过程，用来自适应地改变训练样本的分布，是的弱分类器聚集到哪些很难分类的样本上。
做法是 给每一个训练样本赋予一个权重，在每一轮结束时自动调整权重
优点：
单个评估学习能力较弱的时候 boosting 有一定可能提升模型表现 
在大多数数据集中 boosting 准确性要高于 bagging
缺点:
各个预测函数只能顺序生成，因为后一个模型参数需要前一轮模型的结果 会比较耗时 
会加剧过拟合问题 
目标：降低偏差，提高模型整体的精准度
代表算法：adaboost、gdbt、xgboost 

 

随机森林

from sklearn.ensemble import RandomForestClassifier 

rfc_model=RandomForestClassifier(n_estimators=50,class_weight='balanced',random_state=5).fit(x_train,y_train)
y_test_pred=rfc_model.predict(x_test)

11、网格搜索

#网格搜索使得 f1 得分最高 
from sklearn.metrics import make_scorer
from sklearn.ensemble import RandomForestClassifier as rfc 
from sklearn.model_selection import GridSearchCV

scorer = make_scorer(f1_score, pos_label=0)
c_gamma_range = [0.01, 0.1, 1.0, 10.0]

param_grid = [{'clf__C': c_gamma_range,
               'clf__kernel': ['linear']},
               {'clf__C': c_gamma_range,
               'clf__gamma': c_gamma_range,
               'clf__kernel': ['rbf']}]
#param_grid =[{'n_estimators':range(50,100,10),
#             'max_depth':range(5,20,10)}]

# 初始化网格搜索的方法
gs = GridSearchCV(estimator=rfc(),
                  param_grid=param_grid,
                  scoring=scorer,
                  cv=10,
                  n_jobs=-1)
#用网格搜索方法进行拟合数据
gs = gs.fit(X_train, y_train)
# 输出最优的参数组合
print(gs.best_score_)
print(gs.best_params_)
best_model = gs.best_estimator_

无监督：就是没有目标字段，比如拿到一堆数据不知道数据里面到底有什么信息 我们就可以用聚类 然后找出每一类的特征

12、聚类分析

保持质心点位置不变，更新类别

保持类别不变更新质心点，如此循环，迭代，直到质心点位置不变

损失函数==组内误差和

EM算法 最小化损失函数：E 保持组质心不变，更新类别 M 保持组类别不变，更新质心

方法一：手肘法 随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小，常用clf.inertia_评估指标，他的缺点：这个评价参数表示的是簇中某一点到簇中距离的和，这种方法虽然在评估参数最小时表现了聚类的精细性，但是这种情况会出现划分过于精细的状况，并且未考虑和簇外点的距离最大化

import pandas as pd
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
 
df_features = pd.read_csv('train.csv',encoding='gbk') # 读入数据
'利用SSE选择k'
SSE = []  # 存放每次结果的误差平方和
for k in range(1,9):
    estimator = KMeans(n_clusters=k)  # 构造聚类器
    estimator.fit(df_features[['R','F','M']])
    SSE.append(estimator.inertia_)
X = range(1,9)
plt.xlabel('k')
plt.ylabel('SSE')
plt.plot(X,SSE,'o-')
plt.show()

     方法二：轮廓系数法 轮廓系数的公式为：S=(b-a)/max(a,b)，其中a是单个样本离同类簇所有样本的距离的平均数，b是单个样本到不同簇所有样本的平均。平均轮廓系数的取值范围为[-1,1]，且簇内样本的距离越近，簇间样本距离越远，平均轮廓系数越大，聚类效果越好。那么，很自然地，平均轮廓系数最大的k便是最佳聚类数。

import pandas as pd
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
import matplotlib.pyplot as plt
 
df_features = pd.read_csv('train.csv',encoding='gbk')
Scores = []  # 存放轮廓系数
for k in range(2,9):
    kms = KMeans(n_clusters=k)  # 构造聚类器
    kms.fit(df_features[['R','F','M']])
    Scores.append(silhouette_score(df_features[['R','F','M']],kms.labels_,metric='euclidean'))
X = range(2,9)
plt.xlabel('k')
plt.ylabel('轮廓系数')
plt.plot(X,Scores,'o-')
plt.show()

两者结合看效果更好 

13 关联规则

寻找在同一事件中出现不同项的相关性，通过量化的数字表示物品 X 出现对物品 Y 出现有多大影响，体现交易间相关关系 非因果关系

支持度：项目 X、Y同时出现在总数据集中的概率  support(X→Y) = P(X∪Y)

置信度：先导项已经发生的情况下后继项发生的概率 confidence(X→Y) = P(Y|X)

提升度：用来度量一类商品相对他的一般购买率 此事被购买的可能性大小 lift(X→Y) = P(X∪Y) / P(X)*P(Y)  ；lift<1 二者有负向依赖或替代效应 lift>1 二者正向依赖或互补效应 

14 序列模式

寻找在同一事件中先后出现不同项的相关性 ，有时间关系