深度学习-计算机视觉-基础学习笔记-03

更好的优化方法
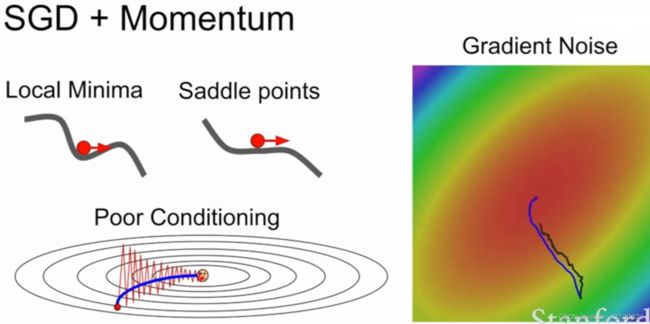
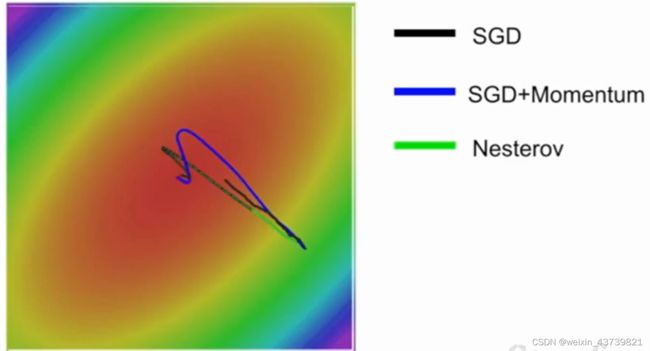
前面提到的随机梯度下降(SGD)在实际使用中会产生很多问题，比如下图中的损失函数对水平方向不敏感而对竖直方向敏感的情况，实际在更高维涉及到非常多的参数时这个问题更明显。

其另一个问题是局部极小值或者鞍点，如下图所示X轴是参数的值,Y轴是损失值，SGD可能陷入局部最优或者鞍点，在那个点上梯度值为0或者接近0所以不会移动或者非常缓慢。

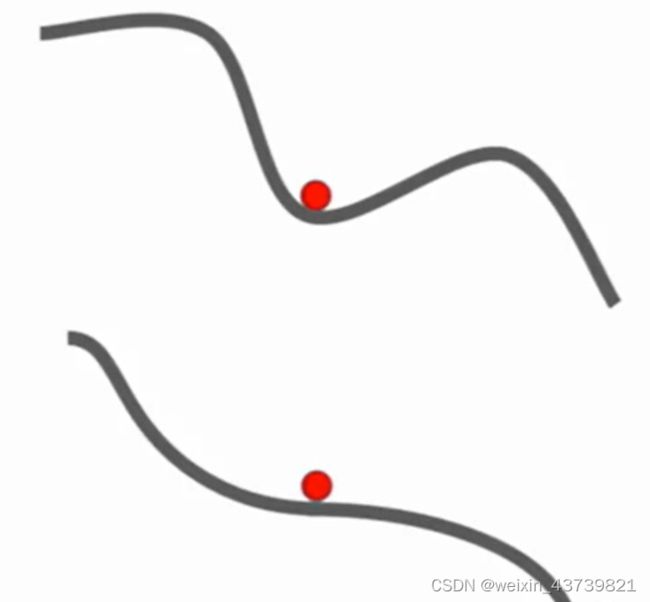
另外一个问题是随机梯度下降每一步是通过小批量的实例来对损失和梯度进行估计，所以在梯度估计中如果存在噪音那么实际上要花费很长时间。

有一个很简单的策略解决上诉问题，就是在随机梯度下降中加入一个动量项。如图右侧所示有一个非常小的方差，称为带动量的SGD，其思想就是加入惯性/速度，使得优化不容易落入局部最优或者停留在鞍点，每一步用摩擦系数ρ(取值一般较大比如0.9)对速度进行衰减然后加到梯度上，保持一个不随时间变化的速度，并且我们将梯度估计添加到这个速度上，然后在这个速度的方向上步进，而不是在梯度的方向上步进。就是这样一个超级简单的思想却解决了上述所有的问题

还有一种变化的动量形式叫做Nesterov加速梯度，或者Nesterov动量，不同于之前是先由速度与当前梯度混合得到当前实际的方向，而是在红点出向速度方向步进，然后评估步进后的位置的梯度，再回到初试位置将俩者混合起来，这种带有"前瞻性"的方法能更快的到达最优点。在凸优化问题上这也有一些很好的理论性质，但是涉及到诸如神经网络的非凸优化问题就会有一些问题了。

Nesterov的公式有点令人感到不便，因为使用SGD优化时一般希望同时计算损失函数和梯度，而其公式会对此造成破坏造成应用上的麻烦，好在我们可以用换元法改进Nestero公式替换变量，就可以同时计算了。

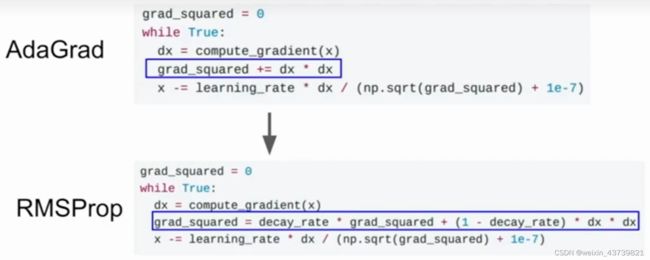
另一种常见的优化策略是AdaGrad算法，核心思想是在优化过程中保持一个在训练过程中的每一步的梯度的平方和的持续估计，现在有了一个梯度平方项，且在训练时会一直累加当前梯度的平方到这个梯度平方项，当我们更新参数向量时会除以这个梯度平方项(加上1e-7防止除以的是0)。所以这样的放缩对于矩阵中条件数很大的情形有什么改进？
举个前面的例子，如果我们有俩个坐标轴，沿一个轴我们有很高的梯度而另一个很小，那么随着累加小梯度的平方，我们会在最后更新参数向量时除以一个小的数字从而加速了在小梯度维度上的学习速度，高维度则相反。那么随着时间的推移平方项越来越大会发生什么？
会使得步长越来越小，所以当目标函数是凸函数的时候训练效果比较好，但是在非凸函数下则不好，容易陷入局部最优。在做神经网络训练时一般不推荐这个算法。

针对AdaGrad的缺陷，有一个AdaGrad的变体叫做RMSProp就考虑到了这个问题。在其中仍然计算梯度平方，但是不是仅仅的在训练中累加梯度平方，而是让平方梯度按照一定比率下降导致其看起来和动量优化法很像，除了我们是给梯度的平方加上动量而不是给梯度本身。
有了RMSProp，在计算完梯度之后取出当前梯度平方项将其乘以一个衰减率通常是0.9或者0.99，然后用1减去衰减率乘以梯度平方并相加。这样仍然保留了AdaGrad在不同轴上梯度不同但维持学习速度的优点。

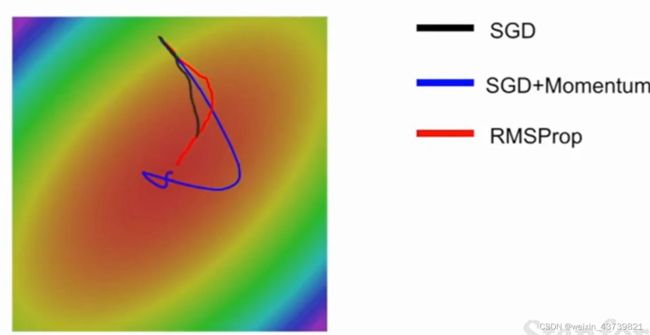
可以看到RMSProp和带动量的SGD效果都比单纯SGD好，但带动量的SGD会先绕过最小值然后又拐回来，RMSProp就一直在调整自己的路线，这样就是在每个维度上做出了大致相同的优化。

以上俩种方法，一个是有速度的概念沿着速度的方向走，一个是梯度平方的概念，这俩种方法看起来都不错，所以也可将他们结合，就是著名的Adam算法。
使用Adam我们更新第一动量和第二动量的估计值，在下图红框里我们让第一动量的估计值等于我们梯度的加权和，第二动量的估计值像AdaGrad和RMSProp一样是一个梯度平方的动态近似值。我们使用第一动量有点类似于速度并除以第二动量或者说第二动量的平方根，所以Adam有点像AdaGrad加上动量或者看起来像动量加上第二个梯度平方，合并了俩者的优点。

但是还有一个问题，在前几步更新时因为第二动量初始化为0导致其特别小所以可能得出很大的步长然后把事情搞砸了，所以Adam算法也增加了偏置校正项避免这个问题。通过使用当前时间步t我们构造了第一和第二动量的无偏估计，用无偏估计来做每一步的更新，这便是Adam的完整形式，一般解决任何问题首要考虑的便是Adam算法，特别是将beta1设为0.9，beta2设为0.999，学习率设为1e-3或者5e-4，无论使用什么网络架构都会从这个设定开始。

学习率的选择技巧
我们不必在整个训练过程中都使用同一个学习率，有时候人们会把学习率沿着时间衰减，有点像是结合了左图中不同曲线的效果，而且是每个图里好的性质。比如在刚开始使用较大的一些学习率，然后在训练的过程中逐渐减小。
一个策略是步长衰减，比如在第十万次迭代时可以衰减一个因子然后继续训练；还有指数衰减，这种是训练时持续衰减。
如果你读论文尤其是残差网络那篇你会经常看到这样的曲线，这样的曲线背后其实就是用步长衰减的学习率，骤降的地方是在迭代时把学习率乘上了一个衰减因子，其思想就是模型已经接近一个不错的取值区域梯度已经很小了，保持原有学习率只能在最优点附近徘徊，但是降低了目标函数仍然能够进一步优化。


TIPS:带动量的SGD的学习率衰减很常见，但像Adam的优化算法就很少用。另一点要指出的是你不应该一开始就用上学习率衰减，开始需要选择一个不错的固定学习率，尝试在交叉验证中调学习率衰减和初试学习率会一头雾水，应该先尝试不用衰减看看会发生什么然后仔细观察损失曲线看看你希望在哪个地方开始衰减。

TIPS:前面提到的都是减少训练误差，但是怎么做来减少训练和测试之间的误差差距呢？
一个快速、笨拙又简单的方法是模型集成，比起用一个模型我们选择从不同的随机初始值上训练10个不同的模型，到了测试时会在10个模型上运行测试数据，然后评价10个模型的预测结果，把这些模型加到一起可以缓解一些过拟合从而提高一些性能，通常是几个百分点，不是很大但却是固定的提升。
在集成学习时有时候超参不是一样的，你可能会尝试不同尺寸的模型不同的学习率不同的正则化策略然后把他们放到一起集成学习。

再发挥一下创造力，有时候可以不用独立地训练不同的模型，你可以在训练的过程中保留多个模型的快照，然后用这些模型来做集成学习，然后在测试阶段把这些多个快照的预测结果做平均。

TIPS：另一个可能用到的小技巧是训练模型的时候对不同时刻的每个模型参数求指数衰减平均值，从而得到网络训练中一个比较平滑的集成模型，之后用这些平滑衰减的平均后的模型参数，而不是截止在某一时刻的模型参数，这叫Polyak平均有时候可能有一些效果但是并不常见。

正则化
除了集成学习，我们希望找到可以提高单一模型的效果，正则化就是，我们在前面介绍过一些，比如L2正则化。
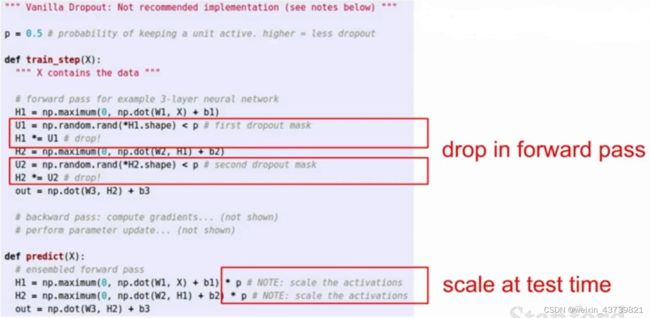
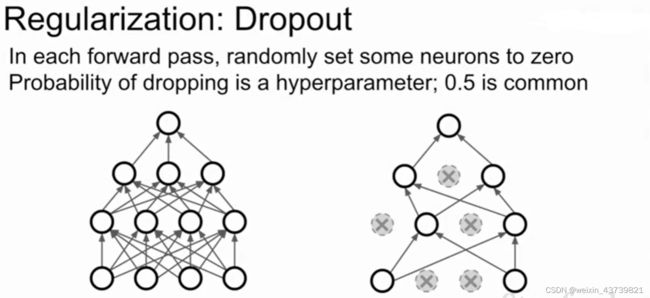
一个在神经网络中特别常用的方法是dropout，其非常简单，每次在网络中正向传播时在每一层随机将一部分神经元置为0(将激活函数的值置为0，每一层都是在计算上一个激活函数的结果乘以权重矩阵，那么下一层激活函数拿到的输入就有一部分是0)，且每次正向传递随机置0的神经元都不完全相同。
在神经网络中一般是在全连接层使用dropout，在卷积神经网络中是随机把某个特征映射整个智0。


为什么这样做有意义，人们认为这样做避免了特征之间的相互适应，假设我们要分类判断是不是猫，可能在网络里一个神经元学到了有一只耳朵，一个学到了尾巴，一个学到了有毛发，然后这些特征被组合到一起来判断是否是猫。但加入dropout之后判断是不是猫时网络就不能依赖这些特征组合一起给出的结果，而是要通过不同的零散的特征来判断，这在某种程度上抑制了过拟合。

另一种关于dropout的解释是这是在单一模型中进行集成学习，因为观察左图，在dropout后是在一个子网络中进行运算，每一种可能的dropout方式产生不同的子网络，所以dropout像是同时对一群共享参数的网络进行集成学习。

因为dropout的随机性，导致我们在测试时有了困难，每一个训练步骤都会创建一个独立的神经网络，因为每一个神经都有可能出现或者不出现，所以总共有2的N次方个可能的网络（N是可丢弃的神经元个数），而在测试时要测试那么多子网然后取平均是完全不可能的，在测试时也不能关闭dropout，训练时加入dropout是为了防止过拟合，若在测试时关闭就是完全不同的模型了。 但是不关闭dropout的话，得到的结果y可能是随机的，所以我们为了让测试时没有任何随机性，我们返回的是dropout的概率乘以输出得到一样的期望值输出，因为每个神经元都有p的概率被舍弃。

总结起来dropout在正向传播中非常简单，只需要加俩行到实现中，随机对一些节点置0。然后在测试时的预测函数内加一点乘法乘你的概率。