连续语音信号的短时倒谱分析及其参数用途

前言

这段时间一直在学习语音信号倒谱分析的相关内容，由于倒谱分析在语音信号处理中应用广泛，导致学习过程中知识点太散、太凌乱，所以自己集中整理了一下倒谱分析在语音信号处理中的一些应用。虽然不全，但是内容量也挺多，那么这次就做一次详细的知识分享吧。
！！！！！！！！！！打个预防针先，内容比较长，希望耐心看完！！！！！！！

基本概念

在学习之前，必须弄清楚几个概念：
什么是倒谱分析？为什么要进行倒谱分析？什么是倒谱？以及倒谱分析有什么用？
首先，对于任意给定的一段语音信号，我们都希望从中获取一些“感兴趣的参数”来做一些处理。最基本的操作就是从时频域进行观察，可以得到时域图和它对应的频谱图或者是语谱图（声纹）。除了这两个处理域之外，还可以从倒谱域进行观察。倒谱分析属于“同态处理”，也叫同态滤波。简单理解就是将卷积关系变换为加性关系，是一个“解卷积”的过程。那么为什么要进行这一转化？
因为目前对连续语音信号分析的基础就是短时分析，将一段语音分成一帧帧信号进行处理。对于一帧语音信号，我们可以认为是平稳的，即在10~30ms内认为信号不发生变化。既然是平稳的，就可以认为一帧语音信号是经过线性时不变系统的输出，即由声门的激励信号与声道冲击响应经过卷积运算形成。相反，如果能够进行卷积的逆运算就能够分离出声门的激励信号和声道冲击响应，而同态处理就是实现“解卷积”的过程，因此倒谱分析也就是为了从语音信号中分离出声门的激励信号和声道冲击响应。那么另一个问题来了，分离出这两个参数要干嘛？
首先必须明白这两个参数是什么？第一、声门激励脉冲信号很好理解就是输入信号。对于经典语音信号模型，语音信号被看成是随机噪声或准周期脉冲序列激励线性时不变系统的输出。当发不同性质的音时，激励情况是不同的。大致上可以分成浊音和清音两种（所有的音）。当发浊音时，可以看成是准周期脉冲序列去激励系统产生输出。发清音则是另一种。对于汉语而言，每个字由声母和韵母组成，其中声母绝大部分为清音，而韵母为浊音，并且韵母还包含声调，具有语义辨识作用，因此对韵母分析具有重要意义。
是不是绕晕了，总结一下。对于汉语而言，我们更多关注韵母部分，韵母是发浊音，而浊音是由准周期脉冲序列激励产生的。也就是说如果我们能够获取发浊音时的准周期脉冲序列的基音周期，就可以人为的合成语音了。因此，分离出的声门激励脉冲信号主要是用来提取发浊音时的基音周期。当有了准确的基音周期之后就可以用来进行语音识别或者是语音合成。
第二，声道冲击响应顾名思义就是包含了声道信息。声道可以被看成是一根具有非均匀截面的声管，在发音的时候将起共鸣器的作用。简单理解就是当激励信号输入到声道中会引起不同的共振特性，产生一组共振频率，也就是共振峰。共振峰是区别不同韵母的重要参数。根据上文可知，对于汉语，不同的韵母代表不同的字。因此，分离出的声道冲击响应主要用来提取共振峰。有了共振峰就可以区别不同的韵母，即识别出不同的汉字，故可以用来做语音识别或者语音合成。
总结：
语音信号的倒谱分析就是用来“解卷积”，将声门激励信号和声道冲击响应从语音信号中分离出来，从而提取相应参数的过程。

倒谱和倒谱参数

1、倒谱

在语音信号处理中，倒谱一般是指信号的对数实幅值谱的逆傅里叶变换，是实倒谱；其量纲是倒频率，单位是时间(s)。其运算过程如下：

首先，经过傅里叶变换由时域的卷积变到频域的相乘，在经过取模（取实数部分）取对数，由乘性关系变为加性关系；最后经过逆傅里叶变换，还原到时域，实现声门激励脉冲与声道冲激响应的分离。注意：这里的“时域”仅仅是广义上而言的，单位是时间。由于进行了取模运算，因此丢失了相位信息，故不能和时域完全等同，命名为倒谱域。

2、复倒谱

与倒谱相对就有所谓的复倒谱。复倒谱也叫对数复倒谱，没有经过取模运算，其他与倒谱过程一致，因此保留着相位信息。复倒谱与倒谱的关系就是：复倒谱是爹，可以由复倒谱推导倒谱；但是不能反着来。
复倒谱主要用来消除语音信号中的混响和回声，用来做语音增强。可以参照以下论文，解释的很详细。简单理解就是，在复倒谱域纯净语音信号分布在靠近原点的位置，而回声的冲激响应分布在远离原点的位置。可以利用这个差异设计复倒谱域上的“低通”滤波器，从而保留纯净语音信号，消除回声和混响。
文献：《复倒谱域语音信号去混响研究》
计算：MATLAB自带了函数可用于直接计算复倒谱，当然也可以根据上文的流程图，逐步编写程序。

[xhat,nd]=cceps(x);%xhat为计算得到的复倒谱，是实序列；
%nd是单位圆延迟，用以保证具有零相位

3、倒谱计算

为了和下面的其他参数进行区分，在此对倒谱参数进行限定，这里主要讨论原语音信号的倒谱。
原语音信号的倒谱计算比较简单，可以采用上面的流程图进行编程操作，或者利用自带的函数进行计算。两种方式的结果肯定是相同的。如下所示：

% %---------------------方法1---------------% %
y1=fft(s1);
y2=log(abs(y1));
y3=ifft(y2);
% %--------------------方法2---------------% %
[xh2,yh2]=rceps(s1);%原信号的倒谱，xh2为倒谱，yh2为最小相位重构

仿真结果：

结论：这两种方法计算得到的结果一样，在此一帧语音信号取了10ms。进一步观察可以发现，此时已经将声门激励信号和声道冲激响应分开。且声道冲激响应在前（黑色矩形框），声门激励信号在后（红色椭圆），因为具有周期特性。
用途：将经过倒谱运算分离出来的声门激励信号和声道冲激响应用来提取其他参数。

(1)、由声门激励信号提取基音周期

由于基音频率的范围分布在60~500HZ内，所以只要在这个频段内找倒谱上的峰值即可。但是需要完成频域到倒频域的转换。代码如下：

% %--------------------提取基音周期---------------% %
[xh2,yh2]=rceps(s1);%原信号的倒谱
% %频域到倒频域的转换（60~500HZ）
lmin=fix(Fs/500);                           % 基音周期的最小值
lmax=fix(Fs/60);                            % 基音周期的最大值
q1=zeros(1,320);
q=xh2(lmin:lmax)';
q1(lmin:lmax)=q;%长度补齐
[r,Lc]=max(xh2(lmin:lmax));%找最大值
T0=(Lc+lmin-1)/Fs;%基音周期（加上延迟量）
F0=1/T0;%基音频率
fprintf('基音周期T0=%5.4f ms\n',T0*1e3);
fprintf('基音频率F0=%5.4f HZ\n',F0);

注意：此时对基音周期的估算仅仅取前1个周期。结果如下：
基音周期T0=4.3750 ms，
基音频率F0=228.5714 HZ。

结论：由图可知，在这一帧10ms语音信号中总共有两个周期。此时，仅仅取了前1个周期，并计算得到对应的基音频率和周期数值如上。

(2)、由声道冲激响应估算共振峰

这一部分的内容见下文，倒谱的频谱参数。

4、倒谱的频谱

根据上文的分析，倒谱是原语音信号的对数实幅值谱的逆傅里叶变换，因此倒谱的频谱就是原语音信号的对数实幅值谱，可以近似等效于原语音信号的频谱，仅仅多了取对数运算。但是需要与共振峰参数区分。共振峰是声道冲激响应的频谱，反映了原语音信号的包络，并认为谱包络的极大值就是共振峰。
在利用声道冲激响应估算共振峰之前需要进行预加重处理，为了将声门脉冲的影响降到最低，只留下声道信息。从上图可知，声道冲击响应分布在倒谱域靠近原点的位置，因此需要在倒频率域添加一个低通窗来提取共振峰参数。代码如下：

s1=y(:,50);%取第50帧信号（有话帧）
u=filter([1 -.99],1,s1); % 预加重
% %--------------------共振峰估算---------------% %
[xh2,yh2]=rceps(u);%原信号的倒谱
Fre=real(fft(xh2));%原信号的幅值谱
cepst=zeros(1,wlen);           
cepstL=4;%窗长（取谱线长度-折中数值）
cepst(1:cepstL)=xh2(1:cepstL);                 
cepst(end-cepstL+2:end)=xh2(end-cepstL+2:end);% 加低通窗
a=fft(cepst);
spect=real(a); %求幅值谱
[Loc,Val]=findpeaks(spect);                      % 寻找峰值（相反输出）
%Loc：共振峰位置
frqz=Fs/wlen/2*(1:wlen);%频率刻度（取一半）
F_q=frqz(Loc);
fprintf('共振频率F=%5.2fHZ \n',F_q);

结果：
共振频率F=725.00HZ 、共振频率F=2012.50HZ 、共振频率F=3300.00HZ 。

结论：从图中可知，声道冲击响应的频谱反映了原信号频谱的包络。此时共有三个共振峰，数值如上所示。故由声道冲击响应能够用来估计共振峰参数。注意这个关系：声道冲激响应的频谱是原语音信号频谱的一部分。

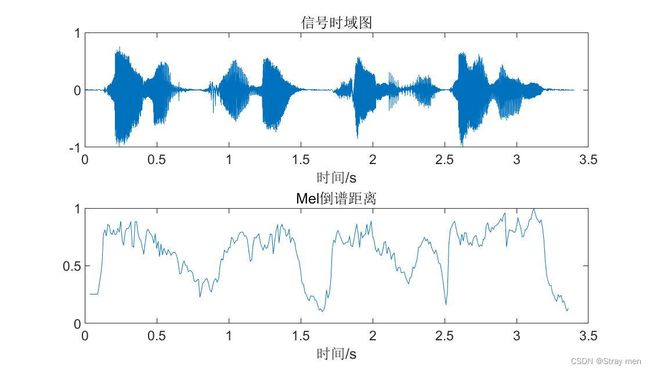
5、倒谱距离

信号倒谱的另一种定义是原语音信号频谱的傅里叶级数展开，因此可以用倒谱距离来表示它们对数谱的均方距离。倒谱距离的计算是各倒谱系数之间的欧氏距离。一般可以用语音信号倒谱距离进行端点检测，即判断语音信号的起始位置和结束位置。该问题主要归结为区别语音和噪声。即根据每个信号帧与噪声帧的倒谱距离的轨迹来进行检测和判断。其中噪声帧采用前导无话帧来估计。更多细节可以查看文献：《含噪语音信号端点检测方法的研究》
代码实现如下：

%加窗分帧
wlen=320;inc=80;
y=enframe(x,wlen,inc)';%分帧
fn=size(y,2);%帧数
% 倒谱距离
for i=1:fn
    c1=y(:,i);%取一帧信号
    c2(:,i)=rceps(c1);%倒谱系数
end
T0=c2(:,1:5);
T0=mean(T0,2);%取前5帧估计噪声帧的倒谱系数
p=24;%取倒谱系数的阶数（1~wlen）
for k=6:fn
    cn=c2(:,k);
    dst0=(cn(1)-T0(1)).^2;
    Dstm=0;
    for j=2:p
        Dstm=Dstm+(cn(j)-T0(j)).^2;
    end
    Dcep(k)=4.3429*sqrt(dst0+2*Dstm);   % 倒谱距离(公式)
end
Dcep(1:5)=Dcep(6);%缺少前5帧
Dcep=Dcep/max(Dcep);%幅值归一化

端点检测结果：

6、Mel频率倒谱系数（MFCC）

Mel频率倒谱系数MFCC实际上就是语音信号在频域经过Mel滤波后的DCT倒谱，其MFCC系数提取的框图如下图所示。

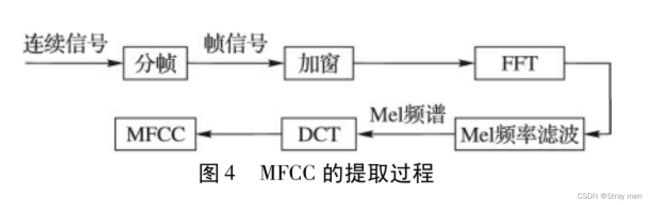
MFCC参数对元音信号具有很好的描述能力，计算量小，实现简单，常用在语音识别中。在此介绍利用MFCC倒谱距离对语音信号进行端点检测。检测的原理参照上面。
代码实现如下：

% MFCC倒谱距离
p=32;%mel滤波器的个数
MFCC=mfcc_m(x,Fs,p,wlen,inc);%头尾都少了两帧
fn1=size(MFCC,1);%少了4帧
frameTime1=frameTime(3:fn-2);% 计算各帧对应的时间
q1=MFCC(:,1:16);%取前16个系数
q0=q1(1:5,:);
q0=mean(q0,1);%取前5帧估计噪声Mel倒谱距离
for k=6:fn1
    qn=q1(k,:);
    dis=0;
    for kk=1:16
        dis=dis+(qn(kk)-q0(kk))^2;
    end
    Dis(k)=sqrt(dis);
end
Dis(1:5)=Dis(6);%补齐前5帧
Dis=Dis/max(Dis);%幅值归一化

端点检测结果：

7、线性预测倒谱系数（LPCC）

线性预测倒谱系数LPCC是对线性预测系数LPC求倒谱得到，该系数也被认为反映了信号谱的包络信息，因此可以看成是对原始信号短时倒谱的一种近似。其计算过程如下：

但是，在编程时是采用递推关系由LPC计算得到LPCC。
代码如下：

function lpcc=lpc2lpccm(ar,n_lpc,n_lpcc)          
% % ————从LPC计算线性预测倒谱系数——————% %
lpcc=zeros(n_lpcc,1);
lpcc(1)=ar(1);  % 计算n=1的lpcc
for n=2:n_lpc   % 计算n=2,...,p的lpcc
    lpcc(n)=ar(n);
    for l=1:n-1
        lpcc(n)=lpcc(n)+ar(l)*lpcc(n-l)*(n-l)/n;
    end
end
for n=n_lpc+1:n_lpcc % 计算n>p的lpcc
    lpcc(n)=0;
    for l=1:n_lpc
        lpcc(n)=lpcc(n)+ar(l)*lpcc(n-l)*(n-l)/n;
    end
end
lpcc=-lpcc;%因为计算LPC采用lpc函数，得到的系数与真实系数相反

思考：LPCC对元音具有较好的描述能力，因此常用在语音识别中。但是其缺点是抗噪声能力较差。因此LPCC倒谱距离用于端点检测中的效果不如其他倒谱距离好。下面给出了利用LPCC倒谱距离对语音信号进行端点检测的代码：

% %--------------计算Lpcc和lpcc倒谱距离------------% %
NIS=5;%噪声帧
p=8;%lpc阶数,取值在(8~12)能够较好表征声道特性(文献)
for i=1:fn
    s1=y(:,i);%取一帧信号
    ar=lpc(s1,p);%计算线性预测系数
    lpcc(:,i)=lpc2lpccm(ar,p,p);%计算LPCC
end
u=lpcc(:,1:NIS);
T0=mean(u,2);%取前NIS帧来估计噪声LPCC倒谱系数
%
for k=(NIS+1):fn
    s2=lpcc(:,k);
    Lpcc_dis=0;
    for kk=1:p
        Lpcc_dis=Lpcc_dis+(s2(kk)-T0(kk)).^2;
    end
    Lpcc_dis1(k)=sqrt(Lpcc_dis);   % lpcc倒谱距离
end
Lpcc_dis1(1:NIS)=Lpcc_dis1(NIS+1);%少了前NIS帧，补偿
Lpcc_dis1=Lpcc_dis1/max(Lpcc_dis1);%幅值归一化

端点检测结果图：


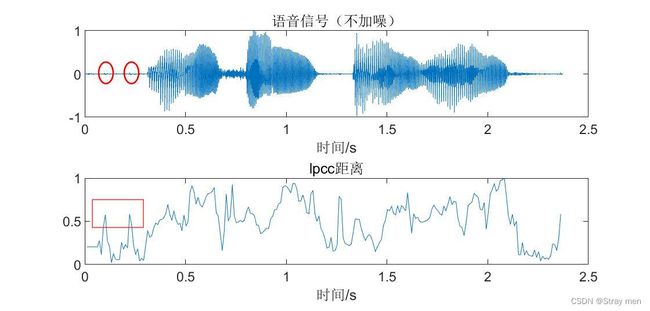
结论：
从以上两个图形中可知，LPCC对噪声比较敏感，抗噪声性能较差。但是在信噪比更高的条件下，其端点检测的效果较好。

8、线性预测Mel倒谱系数（LPMFCC）

根据上文可知，与语音信号的MFCC一样，对于线性预测系数LPC而言也是存在Mel倒谱系数。但是关于它的定义，不同的文献给出了不同的答案，这里给出两种计算方法。

方法1：求解LPMFCC

方法1：先求解LPCC系数，再根据Mel尺度进行非线性变换。文献原文：
《一种改进的基于倒谱特征的带噪端点检测方法》
其计算过程如下：

代码实现：

function Mel_lpcc=Mel_LPCC_m(y,p)
% %----------实现计算lpc的Mel倒谱系数lpcmfcc——————
% %y：加窗分帧后的序列，列为帧
% %p：p为lpc的阶数，一般取值8~12
s1=y(:,1);%取一帧信号
ar=lpc(s1,p);%计算lpc系数
lpcc=lpc2lpccm(ar,p,p);%求lpcc
Cn=lpcc';%倒谱系数（一帧）
n=p;
a=0.35;%Mel转换的拉伸系数，取值0.35或者0.31（文献）

%计算MC_0和MC_1
for j=n:-1:1
    if j+1>n
        MC_0(j+1)=0;
        MC_1(j+1)=0;
        MC_0(j)=Cn(j)+a*MC_0(j+1); 
        MC_1(j)=(1-a^2)*MC_0(j+1)+a*MC_1(j+1);
    else
       MC_0(j)=Cn(j)+a*MC_0(j+1);
       MC_1(j)=(1-a^2)*MC_0(j+1)+a*MC_1(j+1);
       MC_1_0=(1-a^2)*MC_0(1)+a*MC_1(1);%MC_(0)
    end
end
%以上计算会发现MC_1少了一个MC_(0)，调整输出
MC1=zeros(1,9);
MC1(1,2:8)=MC_1(1,1:7);
MC1(1,1)=MC_1_0;
MC=zeros(1,10);

%从MC_2开始递推
for k=2:p
    MC(1,1:9)=MC1;
    for kk=n+1:-1:1
        if kk+1>p+1
            MC(k,kk+1)=0;           
        else
            MC(k,kk)=MC(k-1,kk+1)+a*(MC(k,kk+1)-MC(k-1,kk));
        end
    end
end
% 调整赋值区间，取每阶的第一个系数作为Mel_lpcc输出
for i=1:8
Mel_lpcc(1,i+1)=MC(i,1);
end
Mel_lpcc(1,1)=MC_0(1);

方法2：求解LPMFCC

方法2：是将求解LPC和MFCC的两个过程融合成一个过程，将计算MFCC中信号的功率谱换成LPC的功率谱，然后再进行Mel滤波，计算DCT倒谱。文献原文：
《说话人识别的特征组合方法》
其计算流程图如下：

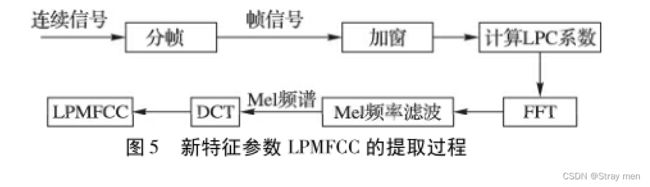
代码实现：

function [ccc,ccc_dis]=mellpcc_m(x,fs,p,wlen,inc,NIS)

% %---------方法2计算LPMFCC----------
% %x:输入信号（不分帧）
% %fs：采样频率
% %p：Mel滤波器的个数
% %wlen：帧长
% %inc：帧移
% %NIS：噪声帧数
% %————————————————
bank=melbankm(p,wlen,fs,0,0.5,'m');% 提取Mel滤波器参数，用汉明窗函数
% 归一化Mel滤波器组系数
bank=full(bank);%全部存储（包含0）
bank=bank/max(bank(:));%幅值归一化
p2=p/2;
% DCT系数,p2*p
for k=1:p2
  n=0:p-1;
  dctcoef(k,:)=cos((2*n+1)*k*pi/(2*p));
end

% 归一化倒谱提升窗口
w = 1 + 6 * sin(pi * [1:p2] ./ p2);
w = w/max(w);

% 预加重滤波器
xx=double(x);
xx=filter([1 -0.9375],1,xx);%补偿高频分量

% 语音信号分帧
xx=enframe(xx,wlen,inc);
np=fix(wlen/2);%计算lpc功率谱的长度
% 计算每帧的MFCC参数
for i=1:size(xx,1)
  y = xx(i,:);%取一帧信号
  s = y' .* hamming(wlen);%加窗平滑
  Lp=lpc(s,p);%计算lpc
  ff=lpcar2pf(Lp,np);%计算lpc功率谱
  c1=dctcoef * log(bank * ff');%Mel滤波后计算DCT
  c2 = c1.*w';
  m(i,:)=c2';
end

%差分系数
dtm = zeros(size(m));
for i=3:size(m,1)-2
  dtm(i,:) = -2*m(i-2,:) - m(i-1,:) + m(i+1,:) + 2*m(i+2,:);
end
dtm = dtm / 3;
%合并MFCC参数和一阶差分MFCC参数
ccc = [m dtm];
%去除首尾两帧，因为这两帧的一阶差分参数为0
ccc = ccc(3:size(m,1)-2,:);

% %-------------计算lpccmcc倒谱距离-------------% %
fn1=size(ccc,1);%少了4帧
q1=ccc(:,1:p);%取前p个lpccmcc系数
q0=q1(1:NIS,:);
q0=mean(q0,1);%取前NIS帧估计背景噪声
for k=(NIS+1):fn1
    qn=q1(k,:);
    dis=0;
    for kk=1:p
        dis=dis+(qn(kk)-q0(kk))^2;
    end
    ccc_dis(k)=sqrt(dis);%倒谱距离
end
ccc_dis(1:NIS)=ccc_dis(NIS+1);%弥补前NIS帧
ccc_dis=ccc_dis/max(ccc_dis);%幅值归一化

利用LPMFCC系数进行端点检测：
代码可以参照以上的方式，仅仅修改系数参数即可，后面我会将所有的程序打包好上传的。
端点检测结果：


结论：与LPCC系数一样，对噪声敏感，抗噪声能力较差。且方法2检测的整体效果优于方法1。但是方法1对噪声帧的抑制能力更强，见图中最左端红色矩形框。LPMFCC在信噪比更高的条件下，检测的效果较好，还是具有实用价值。

9、线性预测误差序列的倒谱

线性预测误差序列是原语音信号与线性预测值之间的差值，由于预测误差序列已经去除共振峰的响应，因此其倒谱将只剩下声门脉冲信号，故可直接用线性预测误差序列的倒谱来估计基音周期。其倒谱如下图所示。

结论：如上图所示，线性预测误差序列的倒谱不再含有声道冲击响应，故可以直接用来提取基音周期。
代码实现：

% %--------------------用误差序列提取基音周期---------------% %
p=12;
a1=lpc(s1,p);
Err=filter(a1,1,s1);%得到误差序列
[D_Err,yh2]=rceps(Err);%计算误差序列倒谱
% %频域到倒频域的转换（60~500HZ）
lmin=fix(Fs/500);                           % 基音周期的最小值
lmax=fix(Fs/60);                            % 基音周期的最大值
q1=zeros(1,320);
q=D_Err(lmin:lmax)';
q1(lmin:lmax)=q;%长度补齐
[r,Lc]=max(D_Err(lmin:lmax));%找最大值
T0=(Lc+lmin-1)/Fs;%基音周期
F0=1/T0;%基音频率
fprintf('基音周期T0=%5.4f ms\n',T0*1e3);
fprintf('基音频率F0=%5.4f HZ\n',F0);

结果：
基音周期T0=4.2500 ms，
基音频率F0=235.2941 HZ。

总结

看到这里你一定头晕的很，我也是。这篇博文写了整整两天，中途还没保存到，又重新写了一遍。。。总之，最后的结果还是好的，希望能够帮助到你们。如果觉得懵的话，建议多看几遍，我都看了无数遍了。加油！最后，我把这篇博文用到的文献、程序都打包好上传了，有需要的可以下载哦~~~~~~~~
！！！！！！！倒谱分析程序包！！！！！！！！！！！