【计算机视觉】NCC匹配算法

1.NCC匹配实验原理

1.1 NCC的基础概念

NCC（normalized cross correlation）算法，归一化互相关匹配法，是基于图像灰度信息的匹配方法。是用来比较两幅图像的相似程度已经是一个常见的图像处理手段。
图像匹配的方法主要有三种：基于灰度，基于特征，基于变换域。
NCC算法可以有效降低光照对图像比较结果的影响。而且NCC最终结果在0到1之间，所以特别容易量化比较结果，只要给出一个阈值就可以判断结果的好与坏。传统的NCC比较方法比较耗时，虽然可以通过调整窗口大小和每次检测的步长矩形部分优化，但是对工业生产检测然后不能达到实时需求，通过积分图像实现预计算，比较模板图像与生产出电子版之间的细微差异，可以帮助企业提高产品质量，减少次品出厂率，把控质量。

1.2 NCC算法的基本原理

对于原始的图像内任意一个像素点(px,py) 构建一个n×n 的邻域作为匹配窗口。然后对于目标相素位置(px+d,py) 同样构建一个n×n大小的匹配窗口，对两个窗口进行相似度度量，注意这里的d有一个取值范围。对于两幅图像来说，在进行NCC NCCNCC计算之前要对图像处理，也就是将两帧图像校正到水平位置，即光心处于同一水平线上，此时极线是水平的，否则匹配过程只能在倾斜的极线方向上完成，这将消耗更多的计算资源。

1.3 相关的数学知识

在数学上NCC代表着归一化的交叉相关性，是数学上统计两组数据之间是否有关系的判断方法，经常用于大数据分析比较流行相关性分析和计算。

• 计算公式如下所示：
  
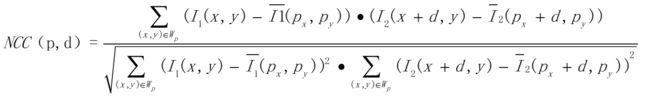
• 其中NCC(p,d) 得到的值得范围将在[−1,1]之间。
• Wp为之前提到的匹配窗口。
• I1(x,y)为原始图像的像素值。
• I1(px,py)为原始窗口内像素的均值。
• I2(x+d,y)为原始图像在目标图像上对应点位置在x方向上偏移d后的像素值。
• I2(px+d,py)为目标图像匹配窗口像素均值。
  若NCC=−1，则表示两个匹配窗口完全不相关，相反，若NCC=1时，表示两个匹配窗口相关程度非常高。

1.4 双目立体匹配流程

1. 采集图像：通过标定好的双目相机采集图像，当然也可以用两个单目相机来组合成双目相机。
2. 极线校正：校正的目的是使两帧图像极线处于水平方向，或者说是使两帧图像的光心处于同一水平线上。通过校正极线可以方便后续的NCC操作。
   2.1 由标定得到的内参中畸变信息中可以对图像去除畸变。
   2.2 通过校正函数校正以后得到相机的矫正变换R和新的投影矩阵P，接下来是要对左右视图进行去畸变，并得到重映射矩阵。
3. 特征匹配：这里便是我们利用NCC做匹配的步骤，匹配方法如上所述，右视图中与左视图待测像素同一水平线上相关性最高的即为最优匹配。完成匹配后，我们需要记录其视差d，即待测像素水平方向xl与匹配像素水平方向xr之间的差值d=xr−xl，最终我们可以得到一个与原始图像尺寸相同的视差图D。
4. 深度恢复：通过上述匹配结果得到的视差图D DD，我们可以很简单的利用相似三角形反推出以左视图为参考系的深度图。计算原理如下图所示：
   
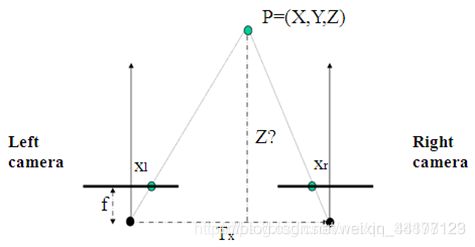
   如图，Tx为双目相机基线，f为相机焦距，这些可以通过相机标定步骤得到。而xr−xl就是视差d。

通过公式z = f * Tx / d可以很简单地得到以左视图为参考系的深度图了。

至此，我们便完成了双目立体匹配。倘若只是用于图像识别，那么到步骤3时已经可以结束了。

1.4 NCC的特点

1. 快速、基于灰度的匹配
2. 鲁棒性
3. 模糊图像
4. 边缘变形图像
5. 有纹理的图像
6. NCC 匹配支持光照变化的情况

• 优点

1. 纹理
2. 对焦不清
3. 形状轻微变形

2.NCC算法实现视差图匹配实验

2.1 实验数据

图片来源：http://vision.middlebury.edu/stereo/data/scenes2003/newdata/teddy/im6.png

2.2 实验代码

# -*- coding: utf-8 -*-
from PIL import Image
from pylab import *
from numpy import *
from numpy.ma import array
from scipy.ndimage import filters
def plane_sweep_ncc(im_l,im_r,start,steps,wid):
    """ 使用归一化的互相关计算视差图像 """
    m,n = im_l.shape
    # 保存不同求和值的数组
    mean_l = zeros((m,n))
    mean_r = zeros((m,n))
    s = zeros((m,n))
    s_l = zeros((m,n))
    s_r = zeros((m,n))
    # 保存深度平面的数组
    dmaps = zeros((m,n,steps))
    # 计算图像块的平均值
    filters.uniform_filter(im_l,wid,mean_l)
    filters.uniform_filter(im_r,wid,mean_r)
    # 归一化图像
    norm_l = im_l - mean_l
    norm_r = im_r - mean_r
    # 尝试不同的视差
    for displ in range(steps):
        # 将左边图像移动到右边，计算加和
        filters.uniform_filter(np.roll(norm_l, -displ - start) * norm_r, wid, s) # 和归一化
        filters.uniform_filter(np.roll(norm_l, -displ - start) * np.roll(norm_l, -displ - start), wid, s_l)
        filters.uniform_filter(norm_r*norm_r,wid,s_r) # 和反归一化
        # 保存 ncc 的分数
        dmaps[:,:,displ] = s / sqrt(s_l * s_r)
        # 为每个像素选取最佳深度
    return np.argmax(dmaps, axis=2)

def plane_sweep_gauss(im_l,im_r,start,steps,wid):
 """ 使用带有高斯加权周边的归一化互相关计算视差图像 """
 m,n = im_l.shape
 # 保存不同加和的数组
 mean_l = zeros((m,n))
 mean_r = zeros((m,n))
 s = zeros((m,n))
 s_l = zeros((m,n))
 s_r = zeros((m,n))
 # 保存深度平面的数组
 dmaps = zeros((m,n,steps))
 # 计算平均值
 filters.gaussian_filter(im_l,wid,0,mean_l)
 filters.gaussian_filter(im_r,wid,0,mean_r)
 # 归一化图像
 norm_l = im_l - mean_l
 norm_r = im_r - mean_r
 # 尝试不同的视差
 for displ in range(steps):
     # 将左边图像移动到右边，计算加和
     filters.gaussian_filter(np.roll(norm_l, -displ - start) * norm_r, wid, 0, s) # 和归一化
     filters.gaussian_filter(np.roll(norm_l, -displ - start) * np.roll(norm_l, -displ - start), wid, 0, s_l)
     filters.gaussian_filter(norm_r*norm_r,wid,0,s_r) # 和反归一化
     # 保存 ncc 的分数
     dmaps[:,:,displ] = s / np.sqrt(s_l * s_r)
 # 为每个像素选取最佳深度
 return np.argmax(dmaps, axis=2)

im_l = array(Image.open(r'D:\testdata\jihe\a1.jpg').convert('L'), 'f')
im_r = array(Image.open(r'D:\testdata\jihe\a2.jpg').convert('L'),'f')
# 开始偏移，并设置步长
steps = 12
start = 4
# ncc 的宽度
wid = 10
res = plane_sweep_ncc(im_l,im_r,start,steps,wid)
import scipy.misc
scipy.misc.imsave('deptha10.png',res)
show()

2.3 实验分析

2.3.1改变steps

• wid=9

steps = 12

steps =20

steps =30

• 由上面实验结果可知，当steps的值越来越大，步长越来越大时，噪点的存在就越来越少，实验图片中的物体纹理愈发明显，但是会丧失许多细节，图片画面过于平滑。所以步长应取适中，以下实验取为20。

2.3.2 改变窗口大小

窗口大小wid=2

窗口大小wid=6

窗口大小wid=9

窗口大小wid=13

窗口大小wid=20

分析小结

由上图的实验结果可以看到，当随着窗口大小不断增大时，可以看到视差图的噪点不断减少，并且图片的细节也不断变少，实验图片中含有的具体细节都有被一定的平滑抹去掉，但由于窗口增大后的边缘逐渐模糊，也更有利于我们判断物体边缘。所以可以显而易见地得出对于wid的取值，我们应该要视情况而定，一般取适中即可，不可过大或过小。
并且，在匹配算法是我们追求的更多是对于位置特征的准确性，需要较多的细节，所以wid取值可以偏小，大约为10即可。