DeepGCNs: Can GCNs Go as Deep as CNNs?

• 论文地址：https://arxiv.org/pdf/1904.03751.pdf
• 源码：deep_gcns_torch
• 来源：ICCV, 2019
• 关键词：GCNPoint Cloud Segmentation, Point Cloud Segmentation

1 前言

该论文聚焦于深度GCN的训练及在点云数据上的分割问题。常见的GCN的层数都比较少，相关研究表明深层的GCN可能会引起如下问题：

• over-smothing，一个连通分量内的结点的表征会趋同
• 较高的复杂度，不利于反向传播
• 梯度消失
  该论文将CNN中的一些技巧引入深层GCN模型的构建，并将其应用在点云数据分割上。

2 问题定义

3 DeepGCN

作者从CNN中引入了三个技巧来解决这个问题：1）Residual learning；2）Dense Connection；3）Dilated Aggregation。

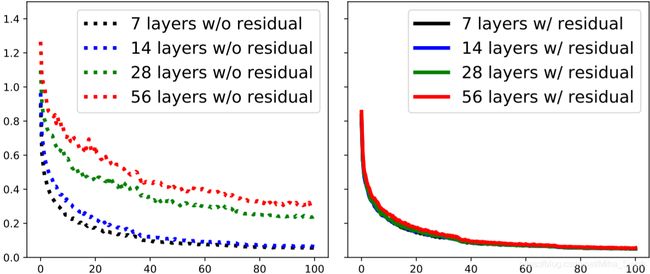
3.1 Residual Learning for GCNs

单纯地堆积卷积层对GCN地效果并没有很大的提升，其中一个原因可能是随着深度的增加，梯度难以反向传播，阻碍了模型的学习。Residual Learning的引入就是为了解决这个问题。
与Residual类似，如果原本要学习的映射为$\mathcal{H}$，残差的映射为$\mathcal{F}$，则残差学习表示如下：
$$\begin{array}{rl}{\mathcal{G}}_{l+1}& =\mathcal{H}({\mathcal{G}}_l,W_l)\\ & =\mathcal{F}({\mathcal{G}}_l,W_l)+{\mathcal{G}}_l={\mathcal{G}}_{l+1}^{res}+{\mathcal{G}}_l\end{array}$$
第$l$层的输出经过$\mathcal{F}$的转换再与第$l$层的输出逐个顶点（vertex-wise）相加得到第$l+1$层的输出。

3.2 Dense Connections in GCNs

DenseNet的提出是为了利用层之间的稠密连接，提高网络中信息的流动，能够对层之间的特征进行重用，形式如下：
$$\begin{array}{rl}{\mathcal{G}}_{l+1}& =\mathcal{H}({\mathcal{G}}_l,W_l)\\ & =\mathcal{T}(\mathcal{F}({\mathcal{G}}_l,W_l),{\mathcal{G}}_l)\\ & =\mathcal{T}(\mathcal{F}({\mathcal{G}}_l,W_l),...,\mathcal{F}({\mathcal{G}}_0,W_0),{\mathcal{G}}_0)\end{array}$$
其中$\mathcal{T}$是一个逐顶点的连接操作，将输入的graph的结点的特征与中间各个GCN层的输出进行拼接。

3.3 Dilated Aggregation inn GCNs

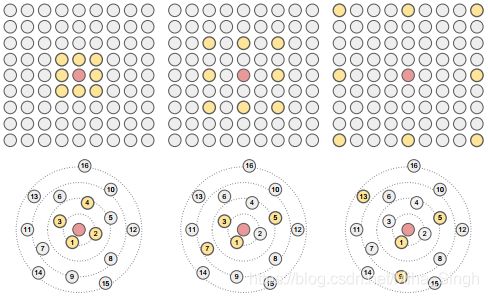
空洞卷积弥补了pooling操作对空间信息的损失，在增大感受野的同时保留了位置信息。在改论文中，作者使用Dilated Aggregation来为每个结点聚集信息，以论文中进行的点云分割实验为例 — 使用Dilated k-NN为每个顶点生成它的邻居。在每个GCN层后，作者使用Dilated k-NN来为每个顶点生成$k$个邻居，这$k$个邻居是从与这个顶点距离最近的$k\times d$个顶点以步长为$d$选择出来的，即顶点$v$的邻居为：${\mathcal{N}}^{(d)}(v)=\{u_1,u_{1+d},u_{1+2d},...,u_{1+(k-1)d}\}$。如下图所示，上部分为dilated卷积，下部分为dilated k-NN，其中选择的$d$分别为1，2，4。在实践中，作者还增加了一点随机性，以$ϵ$的概率随机从$k\times d$中选择$k$个顶点。

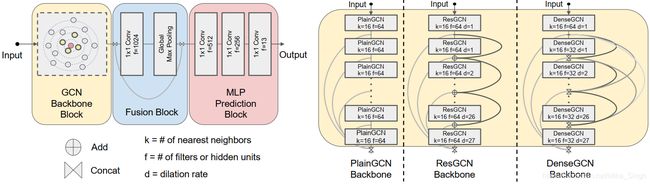
最终，论文中用于点云数据分割的深度GCN架构如下图所示。其中的区别为GCN Backbone Block，这个block有三个选择：1）普通的GCN；2）ResGCN；3）DenseGCN。

4. 总结

• CNN中的技术引入到GCN中，使得训练深层的GCN模型称为可能
• 将GCN应用于点云数据分割

---

---

欢迎访问我的个人博客~~~
以及我的公众号【一起学AI】