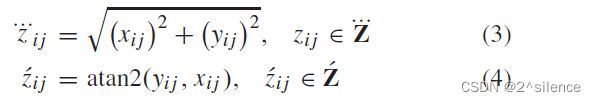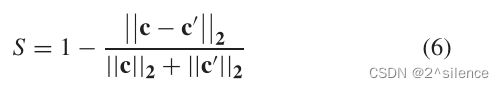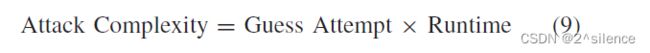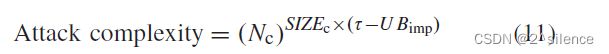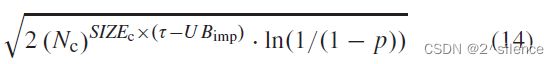2^silence

【论文阅读】Alignment-Robust Cancelable Biometric Scheme for Iris Verification

I. INTRODUCTION

作为替代的BTP解决方案，最近开发的同态加密(HE)(例如，[5])加密生物测定模板，然后在加密的通道中执行模板比较。在客户端[5]中解密模板比较结果。然而，HE方法通常需要很高的计算成本[3]。

虽然对齐实现了所期望得到的性能，但是需要额外计算上的开销。如果有BTP附加操作，则时间复杂度大大增加！

我们所提出的是一个可取消的生物识别方案，它的灵感来自众所周知的梯度直方图[13]。与现有的生物识别工作将HOG视为特征提取方法[14]，[15]不同，我们展示了一个新的个HOG变体，它可以直接将未对齐的虹膜编码特征转换为对齐健壮的可取消模板。在这里，我们概述了选择HoG作为实现我们的可取消生物识别方案的合适方法的主要动机：

HOG是通过对本地信息的统计读数得出的，该信息自然具有对齐-健壮属性。因此，该机制可用于消除转换期间的irisCode对齐问题。
在HOG中使用的多对一映射提供了原始irisCode特征的隐藏，该特征对于BTP中的不可逆性至关重要。

由于所得到的可取消模板对于比对来说是健壮的，因此在模板比较期间不需要特征比对，这提高了识别过程的效率。简而言之，我们的贡献重点如下：

我们设计了一种新的可取消的生物特征识别方案，称为随机增强梯度直方图(R·HOG)，用于保护未对齐的虹膜编码特征。可取消模板对于虹膜代码中的水平移位问题是健壮的；因此，与现有的作品相比，它需要较少的计算开销或存储空间，例如，[16]，[17]。
认证性能在基准CASIA-IrisV3-Internal and CASIA-IrisV4-Thousand数据集上是合理的。此外，使用基准评估框架对R·HOG的不可链接性进行了检验[18]。
我们基于个主要攻击，例如通过输入枚举攻击、Brute强迫攻击、虚假接受攻击和生日攻击，研究了R·hog的安全性和隐私性。

II. RELATED WORK

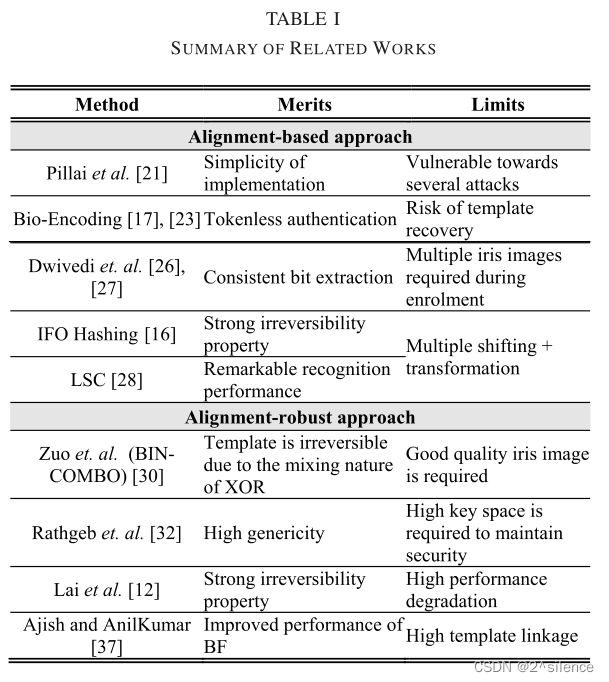
在这一节中，我们回顾了几个与我们的方案相关的虹膜可取消生物特征识别的工作。这些方案被大致分为(A)基于对齐的方法和(B)对齐-稳健方法。在基于对准的方法中，可取消的生物测定方案需要特征对准过程来处理虹膜特征的对准问题。通常，在BTP中有种类型的特征对齐。第一种类型是将可取消生物测定方案应用于多个个移位的生物测定实例，然后将所有移位的个实例变换为可取消模板以用于存储或比较的目的(例如，[16])。另一种类型是基于参考生物特征提取移位不变的生物特征，然后将该移位不变的生物特征变换成个可取消的生物模板(例如，[17])。另一方面，对齐稳健方法是指对于两个个相似的未对齐特征，可以直接产生相似的可取消模板的BTP方案。由于页面长度的要求，我们只关注虹膜可取消的生物特征识别。其他种类的生物识别安全和隐私解决方案可以在[1]、[19]、[20]中找到种。尽管基于深度神经网络(DNN)的种特征在人脸生物识别中受到广泛关注，但虹膜编码仍是目前虹膜识别中使用最多的特征。因此，现有的大多数可取消的生物识别作品都是为了保护虹膜代码而设计的。因此，我们的综述主要集中在个传统的虹膜特征上。

A. Alignment-Based Approach

B. Alignment-Robust Approach

III. PRELIMINARY

A. Histogram of Oriented Gradient (HoG)

方向梯度直方图(HOG)[13]是在计算机视觉(CV)领域中被广泛使用以检测图像中的对象的特征描述符。HOG通过梯度量级和方向来表征对象的局部结构和形状。对于特征形式化的简单视图，使用直方图来统计地记录图像中梯度取向的频率分布(梯度大小)。经典HOG特征提取的过程是：(A)给定图像I，HOG将I分成几个重叠区域(cells)，并计算每个cell的梯度取向的直方图。每个直方图bin由跨越0◦−180◦或0◦−360◦的固定范围方向定义。(B)之后，每个单元将梯度幅度添加到相应的直方图框。(C)最后，应用直方图归一化来提高HOG 特征对光照变化的稳健性。在HOG算法中，将357个重叠的单元格分组为一个block，并在每个block中进行归一化。最后，归一化的块直方图表示HOG描述符。

（一个cell有一个直方图，归一化是在block范围内的）

IV . METHODOLOGY

A. Overview

R·HOG方法可以分解成两个主要组件：a)输入虹膜编码的随机和区别性特征变换。这涉及使用随机生成的变换密钥，以列向量方式增加输入 irisCode。B)多对一映射过程，以将随机化虹膜编码特征变换为不可逆特征向量(可取消模板)。这涉及随机虹膜编码特征的每个不重叠的分区中的梯度出现计数。由于普遍的可消除虹膜模板对于对准是稳健的，所以参考的可撤销虹膜模板可以直接与存储的探测的可撤销虹膜模板比较，没有如上所述的预对齐策略，大大降低了认证过程的时间复杂度。

B. Detailed Approach

1)R·HOG可取消T模板生成：在虹膜验证中，在虹膜扫描过程中，头部倾斜、相机倾斜或眼睛旋转导致提取的虹膜代码[11]中的水平位移位问题。位移位问题可能导致严重的验证性能降低；因此，许多现有的虹膜可消除生物识别方案需要预对准过程来处理该问题。然而，预对准过程可能增加认证过程的时间复杂性。在这篇文章中，我们展示了一种新的使用定向梯度直方图(HOG)来从个未对准的虹膜编码(特征)中导出对齐鲁棒的可取消模板。HOG最初被设计为，用于统计记录像素梯度的频率分布以检测图像中的对象[13]。与现有的只猪生物识别相关工作研究特征提取[14]、[15]不同，我们探索了基于猪的特征在BTP中的非常规用法。提出的随机增强梯度直方图(R·HOG)是基于HOG的特征[13]的扩展，结合了列矢量随机增强和梯度方向分组机制。

在所提出的方案中，通过使用HIS-直方图向量来记录虹膜编码中局部信息(梯度方向)的频率分布来产生对齐鲁棒的生物特征向量(或可取消模板)。为了在之前服务于原始虹膜编码的验证性能，我们对输入的虹膜编码进行了特征增强处理。这样，增加了梯度方向的种群，并且提高了相似输入虹膜编码的可取消模板的相似度。由于虹膜编码的水平位移位，随机增强以列向量的方式执行。由于涉及随机生成的信息，这使得能够更新属性，其中所提出的方案可以为相同的输入虹膜代码产生多个个不相关的可取消模板

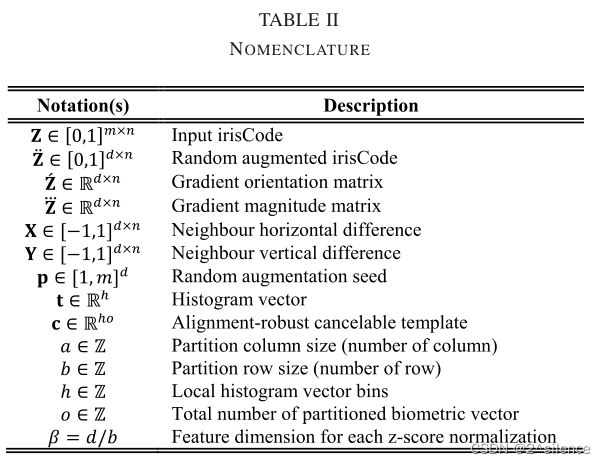
在R·HOG中，每个直方图向量由使用基于方向的直方图来构建，以记录每个 $z_{ij}\in \mathbf{Z}$ 的梯度大小，其中 $\mathbf{Z}\in \left [ 0,1 \right ]^{m\times n}$ 表示生物特征。由于虹膜代码Z是二进制特征只存在‘0’和‘1’。可能的梯度方向是−135◦，−90◦，−45◦、0◦、45◦、90◦、135◦和180◦。为了提高对生物测定信息的隐蔽性，具有180◦差的梯度方向(例如，−45◦和135◦)被分组到相同的直方图柱中。施加的梯度取向分组机制引入多对一映射效应，其中来自个不同方向的梯度幅度被映射到相同的直方图柱中；因此，加强了不可逆属性。此外，定向分组减少了随机增大对可取消模板的大小的影响，其中R·1HoG中的直方图矢量是紧凑数据结构。

给定未对准的虹膜编码 $\mathbf{Z}\in \left [ 0,1 \right ]^{m\times n}$ 和随机的增强种子 $\mathbf{p}\in \left [ 1,m \right ]^{d}$ ，利用变换参数{分区行大小b和分区列大小a}，生成对准稳健的生物测定矢量 $\mathbf{c}\in \mathbb{R}^{ho}$ 的过程如下：

1)列向量随机增强（ $\mathbf{Z}\rightarrow \mathbf{\ddot{Z}}$ ）：对于列向量中的每一个， $\mathbf{z}_{j}=\left [ z_{1j},z_{2j},...,z_{mj} \right ]^{T}$ 在 $\mathbf{Z}\in \left [ 0,1 \right ]^{m\times n}$ 中，随机增强种子 $\mathbf{p}\in \left [ 1,m \right ]^{d}$ 被应用到 $\mathbf{z}_{j}$ 上以产生随机增强的列向量 $\ddot{\mathbf{z}}_{j}=\left [\ddot{z}_{1j},\ddot{z}_{2j},...,\ddot{z}_{dj} \right ]^{T}$ 其中j=1...n表示第j列。具体地说，随机增强过程首先初始化空的 $\ddot{\mathbf{z}}_{j}$ 。在每个 $p\in \mathbf{p}$ 作为 $\mathbf{z}_{j}$ 的索引值的情况下，用替换随机选择每个 $z\in \mathbf{z}_{i}$ 并将其加到 $\ddot{\mathbf{z}}_{j}$ 中。最后，将n个 $\ddot{\mathbf{z}}_{j}$ 水平连接以产生随机扩展虹膜编码 $\ddot{\mathbf{Z}}=\ddot{\mathbf{z}_{1}}||\ddot{\mathbf{z}_{2}}||...||\ddot{\mathbf{z}_{n}}$ 。随机生成的数据(即，p)的参与导致对所提出的方案的的随机化效应；因此，使得能够更新个可取消模板。(d>m会扩大总数据量)

2)梯度取向和大小计算（ $\mathbf{\ddot{Z}}\rightarrow \mathbf{\dddot{Z}} and \mathbf{\acute{Z}}$ ）：在该步骤中，计算对应于每个 $\ddot{z}_{ij}\in \mathbf{\ddot{Z}}$ 的梯度取向和大小，并将其存储在取向矩阵 $\mathbf{\acute{Z}}\in \mathbb{R}^{d\times n}$ 和大小矩阵 $\mathbf{\dddot{Z}}\in \mathbb{R}^{d\times n}$ 中。具体地，每 $\ddot{z}_{ij}\in \mathbf{\ddot{Z}}$ 的相邻元素的水平和垂直差首先用以下公式计算：

左-右，上-下，方向是小的指向大的

其中X和Y表示水平和垂直差矩阵，而rCirShift(.)和cCirShift(.)是行式循环移位函数和列式循环移位函数，例如，rCirShift( $\mathbf{\ddot{Z}}$ ，1)表示行式移位1(即，右移)。在获得X和Y之后，方向和大小矩阵( $\mathbf{\acute{Z}}$ 和 $\mathbf{\dddot{Z}}$ )计算如下：【如果没有rCirShift( $\mathbf{\ddot{Z}}$ ，1)呢？比如说最右边的。难道大小缩小了2？】

其中atan2(.)。是指四象限的逆切线，i=1...d和j=1...n表示元素在矩阵中的位置(行和列)。在我们的例子中，atan2(0，0)的结果被计算为0◦。

3)特征矩阵划分和直方图形式化（ $\mathbf{\dddot{Z}} and \mathbf{\acute{Z}}\rightarrow \mathbf{T}$ ）：对齐稳健变换的核心是使用直方图特征来记录出现的梯度方向对应每一个 $\ddot{z}_{ij}\in \mathbf{\ddot{Z}}$ 。为了提高验证性能，将特征矩阵划分为 o 个不重叠的子矩阵，每个子矩阵的大小为个b×a，其中 $o=\frac{d}{b}*\frac{n}{a}$ 。每个子矩阵被变换为局部直方图向量 $\mathbf{t}\in \mathbb{R}^{h}$ 。以 $\mathbf{\ddot{Z}^{part}}\in \left [ 0,1 \right ]^{b\times a}$ 为分块矩阵，通过添加梯度大小来构造局部直方图向量 $\dddot{z}_{ij}\in \mathbf{\dddot{Z}}$ 到 t 根据的梯度方向 $\acute{z}_{ij}\in \mathbf{\acute{Z}}$ ，其中 h指的是直方图柱的数量（即方向角度被分为几类）；而 $\dddot{z}_{ij}$ 和 $\acute{z}_{ij}$ 是分别对应于每个 $\left ( \ddot{z}^{part} \right )_{ij}\in \mathbf{\ddot{Z}^{part}}$ 的大小和方向值，其中i和j分别是Z和 $\mathbf{\acute{Z}}$ 中元素的行和列数。如前所述，直方图柱被定义为：{−135◦or 45◦}，{−90◦or 90◦}，{−45◦or 135◦}和{0◦or 180◦}。形成 o 个直方图向量，这些直方图向量被垂直组合产生直方图矩阵 $\mathbf{T}=\left [ \mathbf{t}_{1}...\mathbf{t}_{o} \right ]^{T}$ 。

4)Z-Score变换：对于每个列向量 $\mathbf{t}_{j}=\left [ t_{1j},t_{2j},...,t_{oj} \right ]^{T}$ 在 $\mathbf{T}\in \mathbb{R}^{o\times h}$ 中，其中j=1...h表示第j列。将z-Score 归一化应用于 $\mathbf{t}_{j}\in \mathbb{R}^{o}$ （这是一列）以产生归一化的直方图矢量 $\mathbf{\hat{t}}_{j}$ 。每个 $\mathbf{\hat{t}}_{ij}\in \mathbf{\hat{t}}_{j}$ 计算如下：

其中i=1...o表示 $\mathbf{\hat{t}}_{j}$ 中的第i个元素，{μ和σ}是归一化参数。 z-score归一化(具有相同的μ和σ)被应用于 $\mathbf{t}_{j}$ 中的值的每个β维，其对应于 $\mathbf{\ddot{Z}}$ 和 $\mathbf{\acute{Z}}$ 的每个列向量中的直方图的个数目。因此，在归一化每个β维之后，重新计算μ和σ在 $\mathbf{t}_{j}$ 中，其中 $\beta =\frac{d}{b}$ （即每一列在几个不同的块中，就是所有角度一样的重叠在一起，其和就是每一个方向角度的总大小值）。除了将相同的μ和σ用于标准化的目的，直接从生物测定信息(即， $\mathbf{t}_{j}$ )获得μ和σ。因此，只有真正的用户才能重新生成正确的μ和σ以生成 $\mathbf{\hat{t}}_{j}$ 。在这种情况下，归一化可以作为不可逆变换来操作，其中μ和σ在归一化过程之后被处理(对于分析，参见第VI-A节)。在不存储μ和σ的情况下，规格化是可以将不同数据映射到相似的归一化数据的多对一转换。

之后，将h个 $\mathbf{\hat{t}}\in \mathbb{R}^{o}$ 连接以产生对齐稳健的生物测定向量(可取消模板) $\mathbf{c}\in \mathbb{R}^{ho}$ ，其中 $\mathbf{c}=\mathbf{\hat{t}}_{1}^{T}||\mathbf{\hat{t}}_{2}^{T}||...||\mathbf{\hat{t}}_{h}^{T}$ 。图2示出了虹膜码 $\mathbf{Z}\in \left [ 0,1 \right ]^{3\times 5}$ 的R·HOG变换的玩具示例，其中变换参数被设置为b=1，a=3 ，d=6。此外，算法1示出了R·HOG变换的伪代码。在c被破坏的情况下，可以通过用新的随机增强种子变换相同的irisCode Z来生成新的可取消模板。由于c是大的实值和随机化向量，因此新的可取消模板不太可能与旧的可取消模板冲突。

所提出的方案实质上是一种对齐稳健的变换方案，其将未对齐的虹膜编码 $\mathbf{Z}\in \left [ 0,1 \right ]^{m\times n}$ 变换成对齐稳健的可取消模板 $\mathbf{c}\in \mathbb{R}^{ho}$ 。假设RHOG(.)作为变换函数，我们给出下面的语句来概括地描述所提出的R·HOG中的对齐健壮性。

命题1：给定两个向量 $\mathbf{x}\in \left [0,1 \right ]^{m}$ 和 $\mathbf{{x}'}\in \left [0,1 \right ]^{m}$ ，它们具有n个元素方向的水平位移，即 $cirshift\left ( \mathbf{{x}'},n \right )=\mathbf{x}$ ，其中cirshift(.)被称为循环左移函数。RHOG(.)产生x和 $\mathbf{{x}'}$ 的对准稳健输出，使得RHOG(x)≈RHOG( $\mathbf{{x}'}$ )。

讨论：在步骤3变换中，所提出的方案将生物特征变换为直方图向量 $\mathbf{t}\in \mathbb{R}^{h}$ ，该直方图向量对对应于梯度方向的梯度幅度进行统计计数。在这种情况下，实现了多对一的映射，其中相同梯度取向的梯度大小被映射到相同的直方图柱。考虑两个向量的简单例子：x1=[0，1，0]和x2=[1，0，0]，其中cirshift(x1，1)=x2。x1的梯度的大小和方向是 $\mathbf{\dddot{z}}_{1}=\left [ 1,0,1 \right ]$ ， $\mathbf{\acute{z}}_{1}=\left [ 0^{\circ},0^{\circ},180^{\circ} \right ]$ 。对于x2， $\mathbf{\dddot{z}}_{2}=\left [ 0,1,1 \right ]$ ， $\mathbf{\acute{z}}_{2}=\left [ 0^{\circ},180^{\circ},0^{\circ} \right ]$ 。（就是把每个数左移嘛）。在梯度大小和方向的计算中，由于矢量没有顶部和底部相邻单元，所提出的方案将向量的顶部和底部填充‘0’。给定梯度大小(即 $\mathbf{\dddot{z}}_{1}$ 和 $\mathbf{\dddot{z}}_{2}$ )和方向(即， $\mathbf{\acute{z}}_{1}$ 和 $\mathbf{\acute{z}}_{2}$ )，所提出的方案生成直方图向量t1=[0，0，0，2]和t2=[0，0，0，2]，其中直方图箱是：{−135◦或45◦}，{−90◦或90◦}，{−45◦或135◦}，{0◦或180◦}。由于t1=t2，则第四步变换将为x1和x2产生类似的输出c。在该示例中，由于在步骤-4变换期间不存在列矢量，因此直接设置步骤-4，设置c1=t1和c2=t2。给定 $\mathbf{x}\in \left [0,1 \right ]^{m}$ 和 $\mathbf{{x}'}\in \left [0,1 \right ]^{m}$ ，其中 $cirshift\left ( \mathbf{{x}'},n \right )=\mathbf{x}$ ，所提出的随机增强梯度直方图(R·HOG)可以克服未对准问题并产生类似的输出，例如 RHOG(x)≈RHOG( $\mathbf{{x}'}$ )。

通过以上讨论表明，所提出的方案可以将虹膜码 $\mathbf{Z}\in \left [ 0,1 \right ]^{m\times n}$ 转换为对齐鲁棒的可抵消模板 $\mathbf{c}\in \mathbb{R}^{ho}$ 。为了最大化保持验证性能，我们在所提出的方案中使用了两个策略：(A)在STEP-3中，将 $\mathbf{\ddot{Z}}$ 分割成多个部分，然后将其转换为直方图向量(即，t)，该直方图向量将被用来形成可取消模板c；以及(B)对输入 $\mathbf{Z}\in \left [ 0,1 \right ]^{m\times n}$ 执行数据增强，以增加用于直方图形式化的信息。在V-B节中，我们考察了这两种策略的功能保持效果。

C. Comparison of Cancelable Template

一般来说，直方图特征之间的相似性比较可以通过计算欧几里得距离来完成。在方案中，可抵消的虹膜模板是一个串联的直方图向量，因此，我们采用归一化的欧几里德相似性作为比较器。给定使用相同的随机增强种子 $\mathbf{p}\in \left [ 1,m \right ]^{d}$ 生成的参考可消除虹膜模板 $\mathbf{c}\in \mathbb{R}^{ho}$ 和探测可消除虹膜模板 $\mathbf{{c}'}\in \mathbb{R}^{ho}$ ，通过以下方式获得相似性分数S∈[0，1]：

其中 $\left \| . \right \|_{2}$ 是范数函数。S的范围从0到1，表示c和 $\mathbf{{c}'}$ 之间的相似程度。生成的可取消虹膜模板是对准健壮的特征，在整个注册和验证阶段不需要预对齐过程(例如，水平移位[11])。

V. EXPERIMENTS AND DISCUSSIONS

A. Experimental Setup

在这一小节中，解释了实验设置。本文重点提出了一种可撤销的生物识别方案，因此，我们采用了文献[11]、[38]中的软件来提取虹膜编码。所提出的方案使用MA TLAB(V er. R2021b)，并在配备固态硬盘(SSD)500 GB、Intel Core i7 第七代CPU 2.80赫兹和内存DDR4 24GB的PC上进行模拟。

1) Dataset and Comparison Protocol:

为了验证提出的方案，我们使用了两个公开可用的数据集，即CASIA-IrisV3-Internal和CASIA-IrisV4-Thousand[39]。CASIA-IrisV3-Internal是一个数据集，共有个249个受试者(每个受试者都有不同数量的虹膜图像)。为了与现有的虹膜可取消生物特征识别工作(例如，[17]、[26])一致，我们的实验只考虑了左眼。除此之外，我们通过选择具有7个虹膜图像的受试者来子集数据集，以标准化每只眼睛的比较数字。因此，总共提取了868个虹膜编码(124个被试，每个被试×7个样本)用于实验。对于 CASIA-IrisV3-Internal，我们采用[16]中的设置来获得 IrisCode。

--------------

Iris segmentation、Iris texture un-rolling(optional)、Feature extraction、Comparison

[16] Iris segmentation（wahet：加权自适应霍夫和椭圆极变换，现在还包括可调谐版本）

1.加权自适应Hough变换

2.两阶段分割过程（预处理展开为增强的512*64像素图像（两阶段分割算法采用加权自适应Hough变换迭代细化感兴趣区域以找到初始中心点），利用极坐标转换的图像提取极端边缘曲线得到椭圆。）

Feature extraction（lg=> hd for comparison）

3.经过归一化处理，将虹膜区域展开为大小为64×512的固定维数组，即橡皮片模型

4.保留上面50行以形成大小为50×512像素的虹膜纹理。然后对每五行的像素进行平均，以产生新的一维向量。

5.每个向量用一维log Gabor滤波器卷积，生成10×512的复杂虹膜Gabor特征

6.将虹膜Gabor特征的每个复数值相位化为2比特，生成20*512=10240bit

------------------

另一方面，CASIA-IrisV4-Thousand数据集包括总共1000名不同年龄的受试者[39]。在CASIA-IrisV4-Thousand获取虹膜期间的光切换增加了类内变化(例如，镜面反射)[39]。同样，实验中只考虑了个左眼图像。IrisParseNet1[38]被应用到虹膜图像的预处理中，应用 $USIT^{2}$ [11]提取虹膜编码。为了确保符合标准虹膜代码模板创建过程，从数据集中移除多个对象，因为IrisParseNet未能执行虹膜分割，或者相同对象存在重复的虹膜图像(例如，S5013L00和S5013L01)。结果，总共提取了,9500个虹膜编码(950名受试者×每名受试者10个样本)，共个。对于这两个数据集，虹膜编码被生成为Z∈[0，1]20x512。在已报道的实验中，没有考虑可见光谱(VIS)虹膜图像，因为图像质量(基于ISO/IEC 29794)不适合可靠地提取虹膜编码[38]。

在实验中，验证性能的评估主要基于真实/冒名顶替者比较分数分布的等错误率(EER)(%)[40]。给定具有m个对象和每个对象n个数个样本的数据集，下面是比较试验：

类内(或真正的)比较试验：交叉比较来自同一子个对象的可取消模板；因此，为每个受试者生成n个样本的 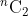$_{}^{n}\textrm{C}_{2}$ 个真实比较分数。
类间(或冒名顶替者)比较试验：交叉比较从不同对象的第一个样本生成的所有可取消模板；因此，总共生成 $_{}^{m}\textrm{C}_{2}$ 个冒名顶替者比较分数。

对于CASIA-IrisV3-内部，2604个真正的比较分数和7626个冒名顶替者的比较分数。对于CASIA-IRISV4-000，有42750个真实比较分数和 450775个冒充比较分数。由于在该方案中随机生成数据(即随机增强种子 $\mathbf{p}\in \left [ 1,m \right ]^{d}$ )，所以实验进行了次(5个不同的p)，获得了平均EER。实验是在令牌被盗场景下进行的。

B. Parameter Estimation

在这一小节中，通过几个实验来验证变换参数对所提出的R·HOG的验证性能的影响。需要注意的是，参数h固定为4，而参数β固定为d b。有三个可调参数，即a、b和d)。

1) Effect of Random Augmentation Size d:

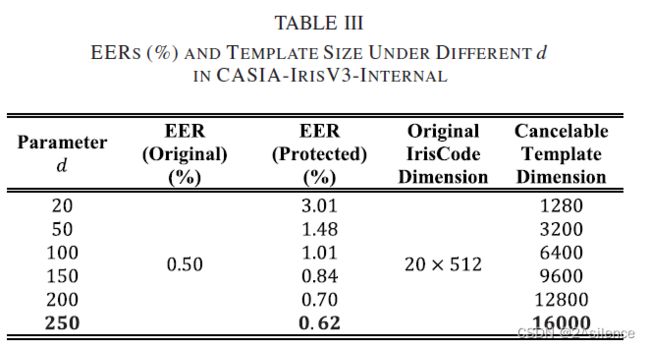
在这一子节中，我们考察了随机增强大小d与验证性能的关系。在所提出的方案中，对输入的虹膜编码进行随机增强，以增加R·HOG中梯度Orienta变换入库的信息量，并使用参数d来控制这一过程。为了验证d，通过设置d从20到250进行实验；而其他参数固定在a=32，b=1。注意到d=20只实现了随机洗牌效果，因为初始行大小虹膜代码m=20。表III列出了不同d在 CASIA-IrisV3-INTERNAL中可取消模板的EER和特征维度。

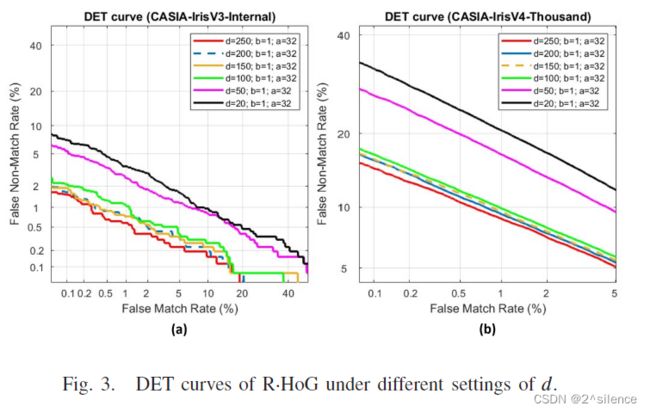
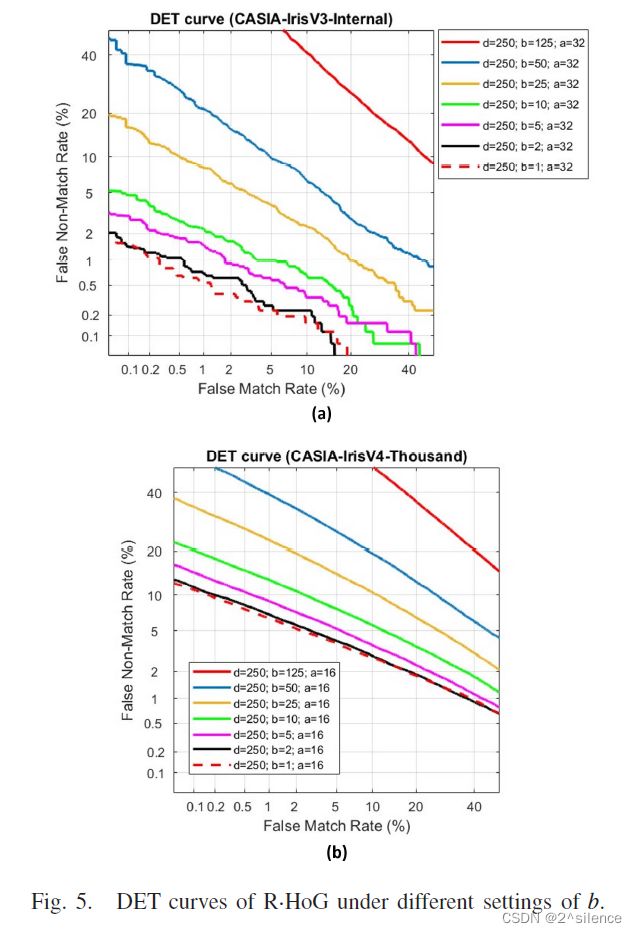
从表中我们观察到，EER随着d的增加而减小。这意味着随机增强正在对改善可撤销模板的识别性能产生效果。从表中可以看出，当d=20(没有增强)时，EER处于最高点，当d从20到100时，EER开始下降。然后，当d≥100时，递减进入较慢的速度.。在d=250时，EER达到低点，其中EER=0.62%。此外，d对两个数据集的影响也可以从下面的检测误差权衡(DET)曲线中观察到。尽管d可以增加，但我们没有考虑d>250，因为这会导致大的可取消模板维度和用于转换的高计算时间。在这里，对于两个个数据集都选择了d=250。

2) Effect of Partition Column Size a, Row Size b:

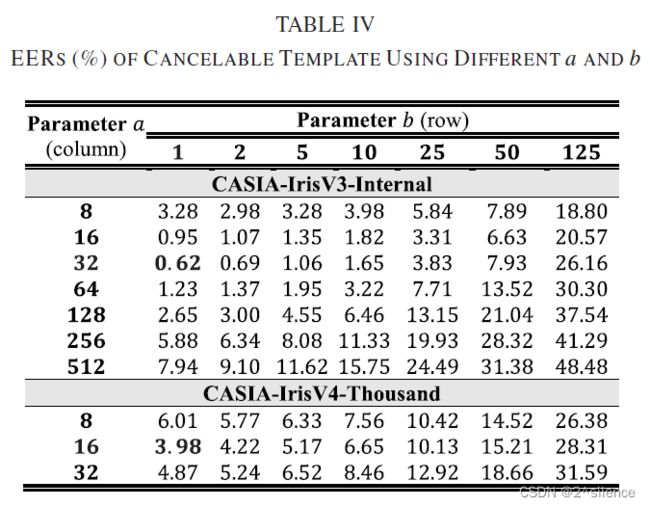
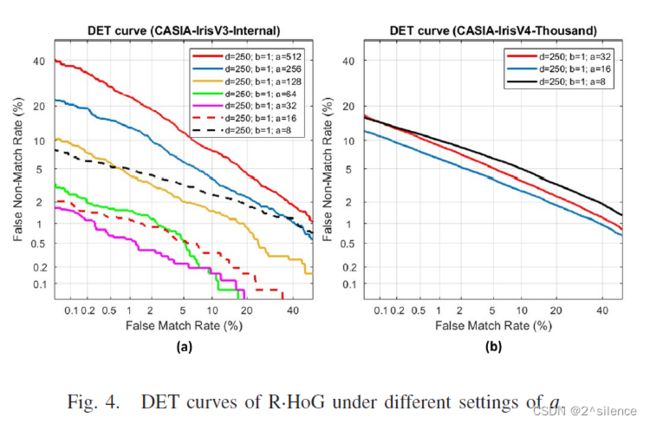
在所提出的方案中，对齐鲁棒的可抵消模板是由来自个虹膜编码的多个非重叠分割块(ZPart∈[0，1]b×a)的局部直方图向量连接而成的。参数a和b用于确定每个分区块的列和行大小。为了验证个不同尺度的分区块，在a和b的不同设置下进行了个实验，而d固定为250。表IV列出了在两个数据集中具有个不同设置的a和b的可取消模板的EER。此外，图4和图5描绘了在不同a和b下的R.Hog 的DET曲线。

正如预期的那样，特征划分可以提高可取消模板的验证性能。从表中可以看出，当710a和710b较大时，EER处于较高的水平。如观察到的，EER随着a和b的减小而逐渐降低。观察到a和b的较低设置可以实现更好的验证性能，因为EER平均低于较高的a和b。因此，建议降低a和b以获得更好的验证性能。由于高a导致高EER，即使在the CASIA-IrisV3-Internal中，因此在随后的实验中不考虑a>32。尽管a的减量可能会降低EER，但不能将a设置为a非常低的值，因为EER开始增加。在我们的上下文中，我们选择{a=32，b=1}作为CASIA-IrisV3-Internal的设置，而选择{a=16，b=1}作为CASIA- IrisV4-Thousand的设置。

3) Summary of Parameter Estimation:

在整个参数估计中，得出了几点结论：

1)增加随机增强大小d可以降低等误码率(EER)(%)。这是因为在直方图公式处理期间，相似虹膜编码的梯度方向的增大；因此， $\mathbf{c}\in \mathbb{R}^{ho}$ 的类内方差可以减小。

2)随机增强大小d导致所产生的可取消模板的模板大小和转换所需的时间的增加。因此，在为d选择合适的值时，必须考虑计算开销和性能之间的权衡。

3)通过分割虹膜代码可以保持原始虹膜代码的验证性能。参数a和b用于确定子块的列和行大小。为了保持原始虹膜编码的验证性能，a和b应该保持在较低的值。还应注意的是，不能将a设置为非常低的值，以防止直方图公式的梯度方向不足。

最后，下表列出了我们的测试组的参数设置摘要。随后的实验是基于列表参数进行的。

C. Verification Performance and Comparison

在这一小节中，我们给出了与ISO/IEC 19795[40]中列出的不同指标相关联的提出的R.HOG的验证性能。

1) Verification Performance of R·HoG：

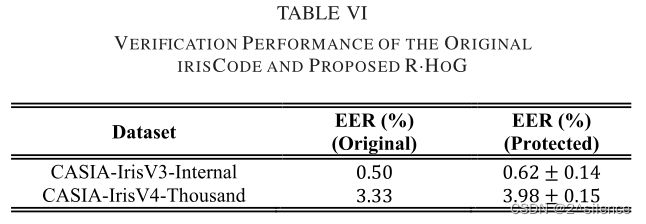
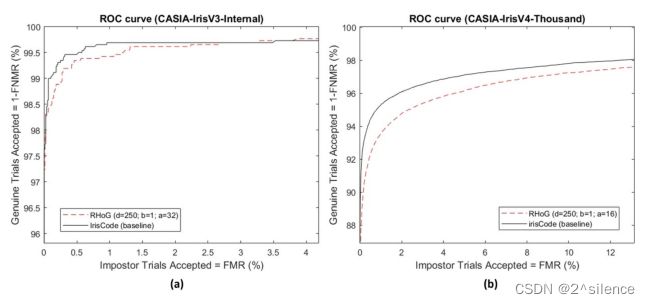
这一小节从(i)平均EER、(ii)接收器工作特性(ROC)/检测误差折衷(DET)曲线和(iii)错误匹配率(FMRS)下的错误不匹配率(FNMR)来呈现所提出的R.HOG 的验证性能。表六以表格形式列出了原虹膜编码和拟议的R.HOG 在EER方面的验证性能。对于CASIA-IrisV3-内部，基于的水平移位获得了原始虹膜编码的验证性能。

对于CASIA-IrisV3-Internal，原始模板是基于±16水平移位获得的。对于CASIA-IrisV4-Thousand，应用±8水平移位与原始模板比较。从列表的EER中可以看出，所提出的R·HOG能够保持原始虹膜编码的验证性能。另一方面，基于描绘的 ROC/DET曲线，观察到R·HOG的验证性能与CASIA- IrisV3-Internal中的原始irisCode相当，而在CASIA-IrisV4-Thousand中观察到更大的退化速率。

2) Comparison to the SOTA Iris Template Protection Methods:

在本小节中，提出的R·HOG模板和现有虹膜模板保护方法的验证性能(EER）是基于CASIA-IrisV3-Internal报道的，由于它被大多数存在的方法所应用。可以观察到，现有的不同作品中实验的虹膜图像数量是不同的，尽管使用的是相同的数据集。例如，我们使用了个CASIA-IrisV3-内部子集，有124个(左眼)受试者个，每个受试者7个样本。此外，现有研究中还没有标准化的比对方案。例如，我们的比较协议包括2604个真正的比较，个分数和7626个冒充比较分数，每个实验中CASIA-IrisV3-Internal。因此，很难在不同研究之间进行公平的比较。然而，为基准目的，报告了拟议计划和现有计划的摘要。如上所述，基于DNN的虹膜验证方法很少见；因此，不考虑。

D. Runtime and Time Complexity

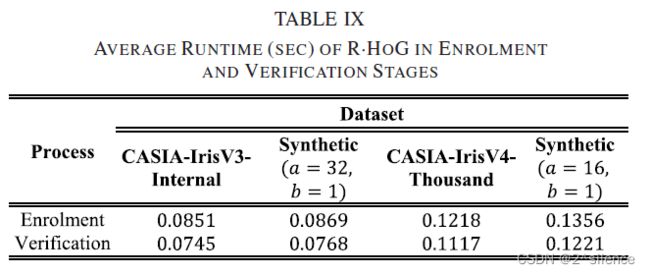
在该子部分中，根据将未对准的虹膜代码转换成对准稳健的可消除虹膜模板的运行时间(秒)来评估提出的方案的计算效率。对注册过程的模拟包括：(i)辅助数据生成和(ii)R·HOG 变换。验证过程包括(i)R·HOG 转换和(ii)模板比对。通过将生产的可撤销模板与预先存储的模板进行比较来模拟模板的比较。对于每个数据集，对所有可用的样本重复实验。对于个实例，在CASIA-IrisV3-Internal上进行总共868了轮测试。此外，利用 SIC-Gen算法4[41]生成由30,000个合成虹膜编码组成的合成数据集。为了生成正确大小的虹膜代码， $\mathbf{Z}\in \left [ 0,1 \right ]^{22\times 512}$ 首先由使用参数{downsampling_every_n_row=3； downsampling_every_n_column=0}生成。最后，去掉 $\mathbf{Z}\in \left [ 0,1 \right ]^{22\times 512}$ 的最后两行，得到 $\mathbf{Z}\in \left [ 0,1 \right ]^{20\times 512}$ 。所有执行的实验的平均运行时间如表9所示。

从表中可以看出，对于所有数据库注册阶段的运行时间比验证阶段长。这主要是由于在每个注册模拟中初始化伪随机数生成器的开销。

除此之外，R·HOG过程的时间复杂度将原始虹膜码转换为可取消模板被表示为Big-O记法。根据算法1，R·HOG可以被构造在四个独立的环路上，每个环路都具有复杂度dn、dn、oab和ho，其中oab=dn，因为 $o=\frac{d}{b}*\frac{n}{a}$ ；ho=o由于h=4是一个常量。因此，R·Hog的时间复杂度可以被估计为O(dn+dn+dn++o)=O(dn)由于dn>o。简而言之，给定维m×n的输入虹膜编码和随机扩展大小d，R·HoG的估计时间复杂度为O(dn)。

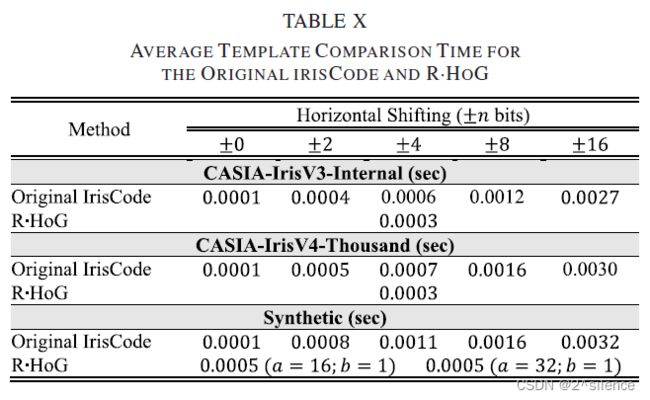
在原始虹膜编码中，使用了归一化的Ha-ming相似性(带水平移位)，而对于R·hog，使用了归一化的欧几里得相似性(直接比较)。因此，还计算并报告了与两种虹膜编码的模板比较的持续时间。模板比较所需的平均时间在表X中报告。

如预期的那样，±n位移位的增量可能增加比较两个给定虹膜码的时间。另一方面，在较低的移位下，R·HOG编码的比较时间与原始虹膜编码的相当。这主要归因于在一对产生的可取消模板之间的直接比较(没有移动)。

VI. SECURITY AND PRIVACY EVALUATION

在这一部分中，我们评估了提出的可取消生物特征识别方案的安全性和保密性。在我们的评估中，假设最坏的情况，其中对手研究变换算法。此外，变换参数(d，a，b，β和h)和辅助信息( $\mathbf{p}\in \left [ 1,m \right ]^{d}$ )也是已知的。为了简单起见，给出了的概述。所提出的方案是：通过d，a，b，h，β和 $\mathbf{p}\in \left [ 1,m \right ]^{d}$ 将未对准的虹膜码 $\mathbf{Z}\in \left [ 0,1 \right ]^{m\times n}$ 变换成可消除的虹膜模板 $\mathbf{c}\in \mathbb{R}^{ho}$ 。

A. Irreversibility Evaluation

不可逆性是指从可取消模板中恢复原始虹膜代码的不可行性。在这个子部分中，使用三个攻击来评估不可逆性，其中攻击者的目标是从个受损的可取消虹膜模板和个随机增强种子中恢复输入的虹膜代码。

1) Inversion Attack via Single Record:

在这一小节中，我们讨论了从单个可取消模板 $\mathbf{c}\in \mathbb{R}^{ho}$ 和随机增强种子 $\mathbf{p}\in \left [ 1,m \right ]^{d}$ 恢复虹膜编码特征 $\mathbf{Z}\in \left [ 0,1 \right ]^{m\times n}$ 的可能性。在开始反转攻击的讨论之前，我们回顾了所提出方案的变换过程。假设有一个输入虹膜编码 $\mathbf{Z}\in \left [ 0,1 \right ]^{m\times n}$ ，该方案首先将 $\mathbf{p}\in \left [ 1,m \right ]^{d}$ 应用于Z的每一列向量，以产生一个随机增强的虹膜编码 $\mathbf{\ddot{Z}}\in \left [ 0,1 \right ]^{d\times n}$ 。然后， $\mathbf{\ddot{Z}}\in \left [ 0,1 \right ]^{d\times n}$ 被分割为o个子矩阵(即 $\mathbf{\ddot{Z}^{part}}\in \left [ 0,1 \right ]^{b\times a}$ )，被转换为直方图向量(即， $\mathbf{t}\in \mathbb{R}^{h}$ )。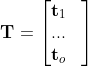然后将直方图向量垂直连接成直方图矩阵 $\mathbf{T}=\begin{bmatrix} \mathbf{t}_{1} & \\ ...& \\ \mathbf{t}_{o} & \end{bmatrix}$ 。最后，将z-score归一化应用于T中的每个列向量 $\mathbf{t}_{j}\in \mathbb{R}^{o}$ ，然后将归一化向量 $\mathbf{\hat{t}}_{j}$ 串联以产生可消除模板 $\mathbf{c}=\mathbf{\hat{t}}_{1}^{T}||\mathbf{\hat{t}}_{2}^{T}||...||\mathbf{\hat{t}}_{h}^{T}$ ，其中 j=1...h，并且针对 $\mathbf{t}_{j}$ 中的值的每个β维重新计算归一化参数。

知道可取消模板 $\mathbf{c}\in \mathbb{R}^{ho}$ 由一组归一化直方图向量形成，其中 $\mathbf{c}=\mathbf{\hat{t}}_{1}^{T}||\mathbf{\hat{t}}_{2}^{T}||...||\mathbf{\hat{t}}_{h}^{T}$ ，对手可以尝试反转每个 $\mathbf{\hat{t}}_{i}$ ，而不是反转可取消模板的每个条目。给定 $\mathbf{\hat{t}}_{i}$ ，攻击者必须遍历从 $\mathbf{\hat{t}}_{i}$ 恢复未归一化的过程，然后从 $\mathbf{t}_{i}$ 恢复梯度大小和方向，并最终恢复 $\mathbf{\ddot{Z}^{part}}$ 。在获得o个 $\mathbf{\ddot{Z}^{part}}$ 后，攻击者可以使用 $\mathbf{p}\in \left [ 1,m \right ]^{d}$ 进行逆置换，恢复原始的irisCode特征 $\mathbf{Z}\in \left [ 0,1 \right ]^{m\times n}$ 。该攻击的第一步是将 $\mathbf{\hat{t}}\in \mathbb{R}^{o}$ 逆归一化为原始 $\mathbf{t}\in \mathbb{R}^{o}$ 。为了简单起见，下面的语句用于讨论归一化向量 $\mathbf{\hat{t}}\in \mathbb{R}^{o}$ 逆变换的可行性。

命题2：给定z-score归一化向量 $\mathbf{\hat{t}}\in \mathbb{R}^{o}$ ，均值μ和标准差σ，对手可以恢复原始向量 $\mathbf{t}\in \mathbb{R}^{o}$ 。

讨论：假设存在向量 $\mathbf{t}\in \mathbb{R}^{o}$ ，z-score归一化使用下面的公式构造归一化向量 $\mathbf{\hat{t}}\in \mathbb{R}^{o}$ ：

其中i=1,...,o，t的恢复(去归一化)可以通过反转归一化过程来实现。在这种情况下，我们可以反转公式(7)来计算 $t_{i}\in \mathbf{t}$ ：

其中i=1,...,o，已知 $\mathbf{\hat{t}}$ 、μ和σ的值，计算 $t_{i}$ 和恢复原始向量 $\mathbf{t}\in \mathbb{R}^{o}$ 是可行的。

命题3：没有μ和σ，从归一化向量 $\mathbf{\hat{t}}\in \mathbb{R}^{o}$ 恢复原始向量 $\mathbf{t}\in \mathbb{R}^{o}$ 是不可行的。

讨论：Z-score归一化是利用输入数据的概率分布来将输入数据转换成重新缩放的数据的过程。通常，Z-score归一化可以为不同的输入产生具有相似尺度的归一化数据。假设有三个向量，即t1=[1，0，1]，t2=[2，0，2]和t3=[3，0，3]，应用z-Score归一化，将μ和σ设置为相应向量的平均值和标准偏差。尽管t1、t2和t3不同，Z-score归一化产生相似的归一化向量，即 $\mathbf{\hat{t}}_{1}$ = $\mathbf{\hat{t}}_{2}$ = $\mathbf{\hat{t}}_{3}$ =[0.58，−1.15，0.58]。因此，在不知道μ和σ的精确值的情况下，很难恢复原始向量t。在这种情况下，z-score归一化可以作为不可逆变换函数来操作。

上述陈述讨论了以逆变换方式从归一化向量恢复原始向量的可行性。它表明，当归一化参数(即，在我们的例子中为μ和σ)未知时，归一化过程是不可逆的。在该方案中，μ和σ是生物统计相关信息，因此真正的用户可以在验证阶段重新生成μ和σ。因此，在生成可取消的模板c之后，处置μ和σ而不存储它们。由于无法获得μ和σ，因此很难为进一步的反演尝试揭示原始向量 $\mathbf{t}_{j}\in \mathbb{R}^{o}$ 。更不用说μ和σ被重新计算，用于每个 $\mathbf{t}_{j}$ 中值的每个β维。除此之外，知道变换密钥(即，随机增q强种子 $\mathbf{p}\in \left [ 1,m \right ]^{d}$ )对于反转攻击是无能为力的，因为在p和 $\mathbf{t}_{j}\in \mathbb{R}^{o}$ 之间没有直接链接。简而言之，对于对手来说，通过单一可取消模板 $\mathbf{c}\in \mathbb{R}^{ho}$ 和随机增加种子 $\mathbf{p}\in \left [ 1,m \right ]^{d}$ 来尝试反转攻击是困难的。

2) Inversion Attack via Multiple Records:

在这个攻击中，攻击者试图基于多个被攻破的可取消的模板 $\mathbf{c}\in \mathbb{R}^{ho}$ 和随机增强种子 $\mathbf{p}\in \left [ 1,m \right ]^{d}$ 恢复虹膜编码特征 $\mathbf{Z}\in \left [ 0,1 \right ]^{m\times n}$ 。在生物模板保护中，这种攻击也被称为通过记录重数(ARM)[7]的攻击。这次攻击比前一次攻击更具破坏性，在这次攻击中，对手获得了额外的信息，并可以尝试利用多个泄露信息的私密链接，并以相反的方式重建虹膜代码 $\mathbf{Z}\in \left [ 0,1 \right ]^{m\times n}$ 。在所提出的方案中，首先应用p和x将 $\mathbf{Z}\in \left [ 0,1 \right ]^{m\times n}$ 变换为随机增广虹膜码 $\mathbf{\ddot{Z}}\in \left [ 0,1 \right ]^{d\times n}$ 。值得注意的是，随机增强是一种置换形式，以在不同的应用中为虹膜码提供随机性。然后，对 $\mathbf{\ddot{Z}}\in \left [ 0,1 \right ]^{d\times n}$ 应用不可逆变换以产生可取消模板 $\mathbf{c}\in \mathbb{R}^{ho}$ 。如上所述， $\mathbf{c}\in \mathbb{R}^{ho}$ 的不可逆性基于z-Score归一化和所处理的参数(即，μ和σ)。利用多个可撤销模板 $\mathbf{c}\in \mathbb{R}^{ho}$ 的额外信息，攻击者可以通过尝试从可撤销模板估计归一化参数，即μ和σ，来进行反转攻击。在此攻击中，攻击者可以尝试使用多个c来推出μ和σ的值，执行进一步的反转攻击。给出 $\mathbf{c}=\mathbf{\hat{t}}_{1}^{T}||\mathbf{\hat{t}}_{2}^{T}||...||\mathbf{\hat{t}}_{h}^{T}$ ，我们通过下面的案例来讨论从多个可取消的模板c的μ和σ中恢复 $\mathbf{\hat{t}}$ 的可行性。

命题4：给定两个来自不同 $\mathbf{c/{c}'}$ 的z-score归一化向量 $\mathbf{\hat{t}}_{1}\in \mathbb{R}^{o}$ 和 $\mathbf{\hat{t}}_{1}^{{}'}\in \mathbb{R}^{o}$ ，它们是从相同的输入 $\mathbf{Z}\in \left [ 0,1 \right ]^{m\times n}$ 生成的，因此很难获得μ和σ恢复原始的 $\mathbf{t}_{1}$ 和 $\mathbf{t}_{1}^{{}'}$

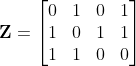讨论：在所提出的方案中，对输入Z应用随机增过程以产生 $\mathbf{\ddot{Z}}$ 。由于随机化过程被应用，在个不同的应用中形成不同的 $\mathbf{\ddot{Z}}$ ；因此， $\mathbf{\hat{t}}_{1}$ 和 $\mathbf{t_{1}^{{}'}}$ 彼此独立并且具有不同的μ和σ的值。因此，对手不能使用 $\mathbf{\hat{t}}_{1}$ 和 $\mathbf{t_{1}^{{}'}}$ 来估计μ和σ。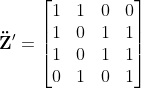给定具有两个增强种子 $\mathbf{p}=\left [ 1,3,2,1 \right ]$ 和 $\mathbf{{p}'}=\left [ 3,2,2,1 \right ]$ 的虹膜编码 $\mathbf{Z}=\begin{bmatrix} 0 &1 &0 &1 \\ 1& 0& 1& 1\\ 1 &1 &0 & 0 \end{bmatrix}$ ，提出的方法首先将z增强为 $\mathbf{\ddot{Z}}=\begin{bmatrix} 0 &1 &0 &1 \\ 1 &1 &0 &0 \\ 1 &0 &1 &1 \\ 0 &1 &0 &1 \end{bmatrix}$ 和 $\mathbf{\ddot{Z}{}'}=\begin{bmatrix} 1 &1 &0 &0 \\ 1 &0 &1 &1 \\ 1 &0 &1 &1 \\ 0 &1 &0 &1 \end{bmatrix}$ 。

在参数{a=4，b=1，β=4，h=4}的情况下，在第四步变换期间首先获得 $\mathbf{t}_{1}=\left \{ 0, 1.4142, 0, 0 \right \}^{T}$ 和 $\mathbf{t}_{1}^{{}'}=\left \{ 1.4142, 0, 1.4142, 0 \right \}^{T}$ 。由于β与 $\mathbf{t}_{1}/\mathbf{t}_{1}^{{}'}$ 的维度相同，因此对于相应的 $\mathbf{t}_{1}/\mathbf{t}_{1}^{{}'}$ 只计算了一组{μ，σ}。t1的μ和σ计算为，μ=0.3536，σ=0.7071；而 $\mathbf{t}_{1}^{{}'}$ 的μ和σ计算为 $\mu {}'$ =0.7071， $\sigma {}'$ =0.8165。因此，来自相同输入Z的 $\mathbf{\hat{t}}_{1}\in \mathbb{R}^{o}$ 和 $\mathbf{\hat{t}}_{1}^{{}'}\in \mathbb{R}^{o}$ 是使用不同的μ，σ和t来生成的。由于归一化参数(即，μ和σ)和非归一化向量(t1和 $\mathbf{t}_{1}^{{}'}$ )是不同的，所以不太可能得到的 $\mathbf{\hat{t}}_{1}$ 和 $\mathbf{t_{1}^{{}'}}$ 冲突。因此，攻击者很难使用 $\mathbf{\hat{t}}_{1}$ 和 $\mathbf{t_{1}^{{}'}}$ 来推断μ和σ的值，并恢复原始 $\mathbf{t}_{1}/\mathbf{t}_{1}^{{}'}$ 。

上述陈述讨论了使用来自不同c的 $\mathbf{\hat{t}}$ 来恢复μ和σ以恢复原始向量t的反转尝试。由于可撤销模板c被建立成 $\mathbf{c}=\mathbf{\hat{t}}_{1}^{T}||\mathbf{\hat{t}}_{2}^{T}||...||\mathbf{\hat{t}}_{h}^{T}$ ，我们可以得出结论，即使攻击破坏了多个可取消模板c，也很难将每个 $\mathbf{\hat{t}}_{i}$ 恢复到 $\mathbf{t}_{i}$ 。此外，直方图形式化期间的梯度大小的多对一映射增加了对手从进一步尝试恢复虹膜编码 $\mathbf{Z}\in \left [ 0,1 \right ]^{m\times n}$ 的难度。在实际应用中， $\mathbf{\ddot{Z}}\in \left [ 0,1 \right ]^{d\times n}$ 是一个大的二进制特征，维度为250×512，不同系统中的 $\mathbf{\ddot{Z}}$ 不太可能发生碰撞；因此，生成的c彼此不相关。此外，由于直方图形式化(多对一映射)的信息损失，在c和p之间没有直接联系。因此，在给定多个c和p的情况下，对手很难尝试反转攻击并恢复 $\mathbf{\ddot{Z}}\in \left [ 0,1 \right ]^{d\times n}$ (或原始 $\mathbf{Z}\in \left [ 0,1 \right ]^{m\times n}$ )。综上所述，分析表明所提出的方案满足不可逆性。

3) Attack via Input Enumeration:

在该攻击中，攻击者旨在通过输入枚举攻击恢复原始虹膜编码 $\mathbf{Z}\in \left [ 0,1 \right ]^{m\times n}$ 。与先前试图通过反向处理可取消的虹膜模板 $\mathbf{c}\in \mathbb{R}^{ho}$ 来恢复原始虹膜编码 $\mathbf{Z}\in \left [ 0,1 \right ]^{m\times n}$ 的攻击不同，攻击要求攻击者猜测虚假的 $\mathbf{Z^{*}}$ ，然后将 $\mathbf{Z^{*}}$ 注入所提出的方案以产生可取消的虹膜模板 $\mathbf{c^{*}}$ 。然后将模板 $\mathbf{c^{*}}$ 与受损的c进行比较。该攻击是简单而有效的，因为它不需要关于变换函数的先验知识。在这种攻击中，当对手能够产生等于c( $\mathbf{c^{*}}$ =c)的 $\mathbf{c^{*}}$ 时，认为Z的恢复是成功的。可以使用以下公式估计攻击的复杂性：

其中，猜测尝试指的是猜测中正确的 $\mathbf{Z^{*}}$ 所需的总轮次，而时间复杂性指的是将 $\mathbf{Z^{*}}$ 转换成 $\mathbf{c^{*}}$ 用于匹配所需的时间。在所提出的方案中，原始虹膜编码 $\mathbf{Z}\in \left [ 0,1 \right ]^{m\times n}$ 是一个二进制矩阵；因此，每个正确条目z∈Z的猜测复杂度是2/2=1，其中z的可能值是0和1。因此，在我们的实现中，对整个Z的猜测尝试等于 $2^{20\times 512}/2$ ，其中20×512是所提取的虹膜编码的维度。对于运行时，我们可以参考Error! Reference source not found。对于各个数据集的平均时间(验证阶段)和参数设置。然而，攻击仍然需要至少( $2^{20\times 512}/2$ )次尝试才能恢复整个Z。从估计值来看，则对手要恢复原始的irisCode Z在计算上是不可行的；因此，所提出的方案显示了对该攻击的抵抗。

B. Security Evaluation

在可撤销生物特征识别中，安全属性是指利用猜测的模板抵抗攻击获得非法访问的方案的的可行性。在这一小节中，我们使用针对生物识别系统的三个主要安全攻击来评估安全属性。

1) Brute-Force (BF) Attack:：

在该攻击中，攻击者穷尽地猜测可取消模板 $\mathbf{c^{*}}$ ，并将 $\mathbf{c^{*}}$ 与参考可取消模板c进行比较。当攻击获得与参考c(c∗=c)相同的c∗时，暴力(BF)攻击被认为是成功的。在我们的文章中， $\mathbf{c}\in \mathbb{R}^{ho}$ 是一个实值向量，大小为ho，值分布为 $\left [ LB_{c},UB_{c} \right ]$ 。UB和LB表示数据集中c的上界和下界。在这种攻击中，对手被要求猜测每个ci∈c，其中i=1,...,ho。每个 $c_{i}^{*}\in \mathbf{c^{*}}$ 的猜测尝试是基于值范围(即， $LB_{c}$ 和 $UB_{c}$ )和实值ci的猜测精度(以小数位表示)来确定的。例如，给定c∈[−0.1，0.1]和小数点后1位的猜测精度，需要3次猜测尝试才能从−0.1, 0.0 和0.1中猜测出正确的c。简而言之，对正确猜测ci∈c的猜测尝试可以表示如下：

整个 $\mathbf{c^{*}}$ 的猜测复杂度估计为 $Guess Complex=GuessAttempt^{size}$ ，其中size指的是 $\mathbf{c^{*}}$ 的大小(对于CASIA-IrisV3-Internal，大小=16000，对于CASIA-IrisV3-Thousand，大小=1061 32000)。下表列出了暴力破解的猜测复杂度。在下表中，最低的猜测精度需要在CASIA-IrisV3-Internal中进行大约 $87^{1600}$ 次的猜测尝试，而对手对的BF攻击是不可能的。据观察，CaSIA-IrisV4-Thousand的估算复杂度更高。这是由于CASIA-IrisV4-Thousand中可取消模板的模板大小增加了。

2) False Acceptance (FA) Attack:

生物识别系统是一种基于阈值的决策系统，当比较分数超过系统阈值 $\tau$ 时授予访问权限。在这种的情况下，敌手可以利用生物特征识别系统的错误匹配率(FMR)来猜测伪可取消模板。错误接受攻击(或字典攻击)需要更少的猜测复杂性，其中它仅需要伪可取消模板 $\mathbf{c^{*}}$ 超过最小阈值 $\tau$ [42]。

传统上，通过计算生成的 $\mathbf{c^{*}}$ 超过 $\tau$ 的攻击复杂度来分析错误接受(FA)攻击，其中 $\tau$ 是等错误率的点[35]。然而，这是不太安全的，特别是当对手最初生成 $\mathbf{c^{*}}$ 时，其处于冒名顶替者分数分布( $UB_{imp}$ )的上界，其中比较分数高于 $\tau$ [43]。因此， $\tau$ 应该始终调得更高。然而，较高的 $\tau$ 会导致较低的真实接受率(GAR)，是安全性和性能之间的权衡。分析了在种不同 $\tau$ 下对该方案的FA攻击。

FA攻击是在最坏情况下进行的，其中对手第一次生成 $\mathbf{c^{*}}$ ，并且c和 $\mathbf{c^{*}}$ 之间的相似性分数等于 $UB_{imp}$ 。此后，敌手扰乱每个 $c^{*}\in \mathbf{c^{*}}$ ，直到S(c， $\mathbf{c^{*}}$ )= $\tau$ 。在我们的文中， $\tau$ 是牺牲一定级别的GAR的阈值，总是高于 $UB_{imp}$ 。给定猜测模板 $\mathbf{c^{*}}$ 和参考模板c，将比较分数S(c， $\mathbf{c^{*}}$ )从 $UB_{imp}$ 增加到 $\tau$ 的攻击复杂性可以估计如下：

其中， $N_{c}$ 是每个c∈c的可能值，而 $SIZE_{c}$ 表示c的大小( $SIZE_{c}$ =ho)。由于c是一个值分布为 $\left [ LB_{c},UB_{c} \right ]$ 的实值向量，我们遵循以下公式在不同的猜测精度(小数位)下计算 $N_{c}$ ：

由于该评估的主要目的是找到合适的 $\tau$ ，使用相对于GAR的不同 $\tau$ 来进行分析。

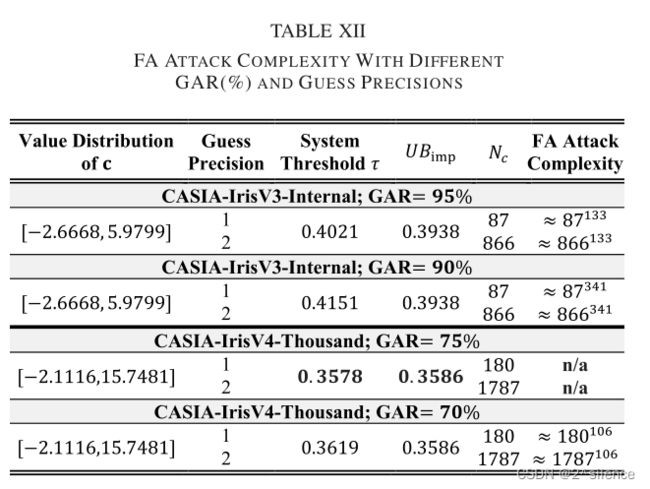
表XII列出了在两个数据集中不同阈值 $\tau$ 下所提出的方案的FA攻击复杂性。从表中，我们观察到与暴力破解攻击相比，攻击复杂性降低了。例如，CASIA-IrisV3-Internal的攻击复杂性从 $87^{16000}$ 降低到 $87^{133}$ ，猜测精度=1。然而，由于估计的攻击复杂性≈ $87^{133}$ 试图获得对系统的访问，对手不可能针对所提出的方案发起FA攻击。另一方面，据观察，CASIA-IrisV4-Thousand需要更高的GAR来达到相当高的安全级别。

3) Birthday Attack:

在BTP中，生日攻击指的是它利用生物特征的冲突来获得对系统的访问权限的攻击[35]。在本文中，生日攻击是攻击者的目标是获得一个假虹膜代码 $\mathbf{Z^{*}}$ 的场景，其中RHOG( $\mathbf{Z^{*}}$ )=RHOG(Z)，其中RHOG(.)。表示R·hog变换函数，Z表示虹膜代码。

这种分析是通过计算攻击的生日界限来确定的[43]。在这里，我们对生日界限(攻击企图)进行简要描述，然后将生日攻击公式化到我们的案例中。假设变换函数f(Z)可以产生H个可能的输出，则获得 $\mathbf{Z^{*}}$ 所需的攻击尝试，使得f(Z)=f( $\mathbf{Z^{*}}$ )计算如下：

其中p是Z和 $\mathbf{Z^{*}}$ 的冲突率，而H指的是f(Z)的输出的可能组合。

在我们的文中，生日攻击作为FA攻击的扩展来进行，其中对手最初猜测 $\mathbf{Z^{*}}$ 以产生 $\mathbf{c^{*}}$ ，其最初落在冒名顶替者分数分布的上界中( $UB_{imp}$ )。然后，对手扰乱每个 $z_{ij}\in \mathbf{Z^{*}}$ ，直到S(c，c∗)= $\tau$ ， $\tau$ 是可取消模板的系统阈值。由于存在 $\left ( N_{c} \right )^{SIZE_{c}}$ 个可能的 $\mathbf{c{}'}$ ，其中 $SIZE_{c}$ 是c的模板的大小，因此生日界限可以如下估计：

其中p是 $\mathbf{Z^{*}}$ 和Z之间的冲突率。在我们的情况下，p被假设为个输入Z的错误匹配率(FMR)。 $N_{c}$ 是可能的c∈c的数目，其是基于第VI.B.2节中的等式(13)计算的。在分析中，没有考虑猜测精度>1。

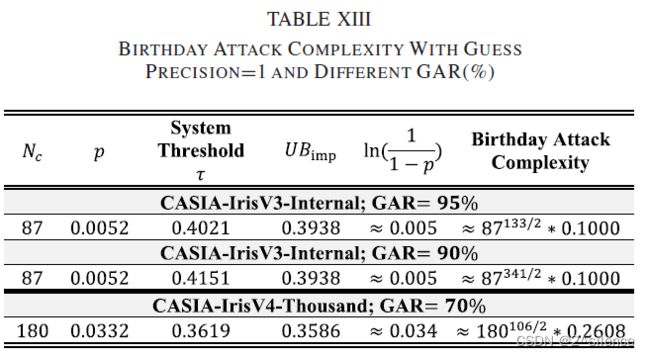
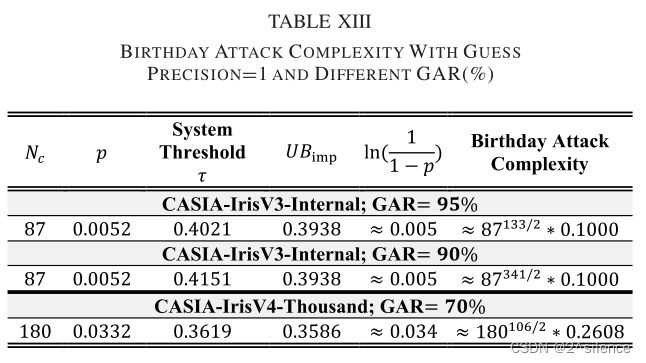
表 XIII列出了两个数据集相对于系统阈值不同的真实接受率(GAR)的攻击复杂性。从表中我们观察到，与虚假接受攻击( the false acceptance attack)相比，攻击的复杂性降低了。然而，通过将 $\tau$ 调整为更高的值，可以进一步提高安全强度。例如，在GAR=95%下适当调优系统 $\tau$ 的，系统在CASIA-IRISV3-INTERNAL中显示了相当大的安全级别(估计的生日边界为≈87133/2.0.1)。简而言之，系统开发人员在部署建议的R·HOG时必须考虑GAR和安全级别。

C. Unlinkability Evaluation

不可链接性对于可撤销的生物特征方案是重要的，对于相同的生物特征输入以允许可取消模板的再现，同时最小化不同应用中的多个生产的可取消模板之间的链接。在这一小节中，我们基于源于[18]的基准分析框架来论证R·HOG的不可链接性。具体地，该评估框架依赖于两个指标，即 $D_{\leftrightarrow }\left ( s \right )$ 和 $D_{\leftrightarrow }^{sys}$ 来量化可取消模板的链接水平：

Local measure: 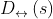$D_{\leftrightarrow }\left ( s \right )$ 是根据似然比在配对/非配对分数(mated/ non-mated score)分布之间找到的局部分数指标[18]。
Global Measure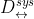： $D_{\leftrightarrow }^{sys}$ 评估整个系统的不可链接性；因此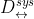， $D_{\leftrightarrow }^{sys}$ 用于基准目的[18]。

这些指标是根据配对/非配对的个样本得分分布(the mated/non-mated samples score distributions)[18]来计算的，该分布是通过以下个比较试验产生的：

Mated samples comparison trial: 交叉比较从每个虹膜产生的个可取消模板c。
Non-mated samples comparison trial：交叉比较不同虹膜的第一个样本产生的个c。

在两个比较试验中，使用不同的 $\mathbf{p}\in \left [ 1,m \right ]^{d}$ 来生成每个c，以模拟可取消模板c来自不同应用的情况。我们使用5组不同的个随机增强种子p为每个irisCodez生成最多5cs。 $D_{\leftrightarrow }^{sys}$ 范围从0到1，这表明可取消模板的链接水平[18]。简而言之，计算的 $D_{\leftrightarrow }^{sys}$ 应该保持尽可能低的水平，以提供的合理的不可链接性。在整个不可链接性评估中，可取消的个模板是基于第V.B.3节中讨论的个参数生成的。评估框架的参数被设置为1[18]。图8示出了关于交配/非交配分数分布和 $D_{\leftrightarrow }^{sys}$ 的不可链接性分析的结果。绘制的得分分布表明，由于 $D_{\leftrightarrow }^{sys}$ 接近于0，所提出的方案达到了不可链接性要求。此外，交配样本和非交配样本的得分分布高度重叠。计算的 $D_{\leftrightarrow }^{sys}$ 还显示更新的可取消模板彼此不相关，因为来自相同虹膜的可取消模板(使用不同的密钥)具有低链接。

VII. CONCLUSION

在本文中，我们提出了一种对齐稳健的可取消的生物特征识别方案，称为R·HOG用于虹膜模板保护。该方法借鉴了方向梯度直方图的思想，克服了虹膜特征的预对齐问题，生成了一个对齐稳健的可抵消虹膜模板，用于有效的比对。两个主要机制：利用列矢量随机增强和定向分组机制，使R·HOG具有性能保持性和不可逆性。在最坏情况下验证了的识别性能，其识别性能可以接受，的平均EER=0.62%(CASIA-IrisV3-Internal)，的EER=3.98%(CASIA-IrisV4-Thousand)。除此之外，我们证明了R.HOG可撤销生物识别方案能够抵抗主要的安全和隐私攻击，例如虚假接受攻击和生日攻击。通过牺牲一定的水平的真实接受率(GAR)来换取较高的阈值 $\tau$ ，该方案可以提供更强的安全强度。此外，我们还利用基准评估框架证明了所提出的方案满足不可链接性。更重要的是，R·HOG享受了快速相似性比较的优点，其中生成的可取消模板不需要预对齐。由于所提出的方案是针对未对齐的二进制特征而设计的，我们可以将所提出的方案传播到其他生物特征模式，例如手指静脉。此外，我们还概述了其他可能的扩展：对齐稳健用于生物特征识别任务的可撤销索引；以及在多模式系统上的适配以解决特征不兼容问题。

你可能感兴趣的:(论文阅读)

《互联网时代教师自主成长的模式研究》论文阅读与思考2 宁超群
2.第二部分教师自主成长的模式建构，实质上是对新网师底层逻辑的描述。你认为，新网师的培训模式与传统常见的培训模式有哪些区别？这些区别有什么意义或价值？读完第二部分后，你对新网师有哪些新的认识或理解？你认为新网师目前哪些方面做得好，哪些方面做得还不够？答：我认为新网师的培训模式与传统常见的培训模式有以下区别：（1）培训对象的参与动机不同。新网师学员的参与是自觉自愿、积极主动，而传统培训更多是被迫参与
【定位系列论文阅读】-Patch-NetVLAD: Multi-Scale Fusion of Locally-Global Descriptors for Place Recognition（一）醉酒柴柴论文阅读学习笔记
这里写目录标题概述研究内容Abstract第一段（介绍本文算法大致结构与优点）1.Introduction介绍第一段（介绍视觉位置识别的重要性）第二段（VPR的两种常见方法，本文方法结合了两种方法）第三段（本文贡献）第四段（为证明本文方法优越性，进行的测试以及比较）2.RelatedWork相关工作第一段（介绍早期与深度学习的全局图像描述符）第二段（介绍局部关键点描述符）第三段（局部描述符可以进一
论文阅读笔记（十九）：YOLO9000: Better, Faster, Stronger __Sunshine__ 笔记 YOLO9000 detection classification
WeintroduceYOLO9000,astate-of-the-art,real-timeobjectdetectionsystemthatcandetectover9000objectcategories.FirstweproposevariousimprovementstotheYOLOdetectionmethod,bothnovelanddrawnfrompriorwork.Theim
论文阅读笔记: DINOv2: Learning Robust Visual Features without Supervision 小夏refresh 论文计算机视觉深度学习论文阅读笔记深度学习计算机视觉人工智能
DINOv2:LearningRobustVisualFeatureswithoutSupervision论文地址:https://arxiv.org/abs/2304.07193代码地址:https://github.com/facebookresearch/dinov2摘要大量数据上的预训练模型在NLP方面取得突破，为计算机视觉中的类似基础模型开辟了道路。这些模型可以通过生成通用视觉特征(即无
周四 2020-01-09 08:00 - 24:30 多云 02h10m 么得感情的日更机器
南昌。二〇二〇年一月九日基本科研[1]:1.论文阅读论文--二小时十分2.论文实现实验--小时3.数学SINS推导回顾--O分4.科研参考书【】1)的《》看0/0页-5.科研文档1)组织工作[1]:例会--英语能力[2]:1.听力--十分2.单词--五分3.口语--五分4.英语文档1)编程能力[2]:1.编程语言C语言--O分2.数据结构与算法C语言数据结构--O分3.编程参考书1)陈正冲的《C语
【论文阅读】Mamba:选择状态空间模型的线性时间序列建模（二） syugyou Mamba状态空间模型论文阅读
文章目录3.4一个简化的SSM结构3.5选择机制的性质3.5.1和门控机制的联系3.5.2选择机制的解释3.6额外的模型细节A讨论：选择机制C选择SSM的机制Mamba论文第一部分Mamba:选择状态空间模型的线性时间序列建模(一)3.4一个简化的SSM结构如同结构SSM，选择SSM是单独序列变换可以灵活地整合进神经网络。H3结构式最知名SSM结构地基础，其通常包括受线性注意力启发的和MLP交替地
SAFEFL: MPC-friendly Framework for Private and Robust Federated Learning论文阅读笔记慘綠青年627 论文阅读笔记深度学习
SAFEFL:MPC-friendlyFrameworkforPrivateandRobustFederatedLearning适用于私有和鲁棒联邦学习的MPC友好框架SAFEFL，这是一个利用安全多方计算(MPC)来评估联邦学习(FL)技术在防止隐私推断和中毒攻击方面的有效性和性能的框架。概述传统机器学习（ML）：集中收集数据->隐私保护问题privacy-preservingML(PPML)采
MixMAE(MixMIM):用于分层视觉变压器有效预训练的混合和掩码自编码器论文阅读皮卡丘ZPC 扩散模型阅读论文阅读
论文:MixMAE(arxiv.org)代码:Sense-X/MixMIM:MixMIM:MixedandMaskedImageModelingforEfficientVisualRepresentationLearning(github.com)摘要:本文提出MixMAE(MixedandmaskAutoEncoder)，这是一种简单而有效的预训练方法，适用于各种层次视觉变压器。现有的分层视觉变
【论文阅读】LLM4CP: Adapting Large Language Models for Channel Prediction（2024） Bosenya12 科研学习论文阅读语言模型人工智能信道预测时间序列
摘要Channelprediction（信道预测）isaneffectiveapproach（有效方法）forreducingthefeedback（减少反馈）orestimationoverhead（估计开销）inmassivemulti-inputmulti-output（大规模多输入输出）(m-MIMO)systems.However,existingchannelpredictionmet
【论文阅读】AugSteal: Advancing Model Steal With Data Augmentation in Active Learning Frameworks（2024） Bosenya12 科研学习模型窃取论文阅读模型窃取模型提取数据增强主动学习
摘要Withtheproliferationof（随着）machinelearningmodels（机器学习模型）indiverseapplications,theissueofmodelsecurity（模型的安全问题）hasincreasinglybecomeafocalpoint（日益成为人们关注的焦点）.Modelstealattacks（模型窃取攻击）cancausesignifican
Bert系列：论文阅读Rethink Training of BERT Rerankers in Multi-Stage Retrieval Pipeline 凝眸伏笔 nlp 论文阅读 bert reranker retrieval
一句话总结：提出LocalizedContrastiveEstimation(LCE)，来优化检索排序。摘要预训练的深度语言模型(LM)在文本检索中表现出色。基于丰富的上下文匹配信息，深度LM微调重新排序器从候选集合中找出更为关联的内容。同时，深度lm也可以用来提高搜索索引，构建更好的召回。当前的reranker方法并不能完全探索到检索结果的效果。因此，本文提出了LocalizedContrast
A Tutorial on Near-Field XL-MIMO Communications Towards 6G【论文阅读笔记】 Cc小跟班【论文阅读】相关论文阅读笔记
此系列是本人阅读论文过程中的简单笔记，比较随意且具有严重的偏向性（偏向自己研究方向和感兴趣的），随缘分享，共同进步~论文主要内容：建立XL-MIMO模型，考虑NUSW信道和非平稳性；基于近场信道模型，分析性能（SNRscalinglaws，波束聚焦、速率、DoF）XL-MIMO设计问题：信道估计、波束码本、波束训练、DAMXL-MIMO信道特性变化：UPW➡NUSW空间平稳–>空间非平稳（可视区域
论文阅读：scMGCA----模型方法 dundunmm 论文阅读论文阅读人工智能聚类生物聚类单细胞聚类单细胞分析
Yu,Z.,Su,Y.,Lu,Y.etal.Topologicalidentificationandinterpretationforsingle-cellgeneregulationelucidationacrossmultipleplatformsusingscMGCA.NatCommun14,400(2023).https://doi.org/10.1038/s41467-023-36134
论文阅读：scHybridBERT dundunmm 论文阅读机器学习人工智能神经网络深度学习单细胞基因测序
ZhangWei,WuChenjun,XingFeiyang,JiangMingfeng,ZhangYixuan,LiuQi,ShiZhuoxing,DaiQi,scHybridBERT:integratinggeneregulationandcellgraphforspatiotemporaldynamicsinsingle-cellclustering,BriefingsinBioinform
【论文阅读】Purloining Deep Learning Models Developed for an Ultrasound Scanner to a Competitor Machine Bosenya12 科研学习模型窃取论文阅读深度学习人工智能模型安全
TheArtoftheSteal:PurloiningDeepLearningModelsDevelopedforanUltrasoundScannertoaCompetitorMachine（2024）摘要Atransferfunctionapproach（传递函数方法）hasrecentlyproveneffectiveforcalibratingdeeplearning(DL)algorit
《Motion Forecasting with Dual Consistency and Multi-Pseudo-Target Supervision》论文阅读之DCMS 山水之间2018 无人驾驶 Paper Reading 大数据轨迹预测自动驾驶人工智能
目录摘要1简介2相关工作3.方法3.1结构3.2双重一致性约束3.3多伪目标监督3.4学习4实验4.1实验装置4.2实验结果4.3消融研究4.4泛化能力5限制6结论DCMS：具有双重一致性和多伪目标监督的运动预测香港科技大学暂无代码。摘要我们提出了一种具有双重一致性约束和多伪目标监督的运动预测新框架。运动预测任务通过结合过去的空间和时间信息来预测车辆的未来轨迹。DCMS的一个关键设计是提出双重一致
时序预测相关论文阅读笔记能力越小责任越小YA 论文阅读笔记时序预测 Transformer
笔记链接：【有道云笔记】读论文（记录）https://note.youdao.com/s/52ugLbot用于个人学习记录。
【论文阅读|cryoET】本周粗读汇总吃吃今天努力学习了吗冷冻电镜三维重建论文阅读
论文1：CryoDRGN-ET：深度重建生成网络以可视化细胞内动态生物分子Abstract虽然冷冻电子断层扫描可以以分子分辨率揭示结构，但图像处理算法仍然是解决原位生物分子结构异质性的瓶颈。本文介绍CryoDRGN-ET用于cryoET断层图的异质重建。CryoDRGN-ET直接从子断层扫描倾斜系列图像中学习三维密度图的深度生成模型，并且可以捕获成分和构象不同的状态。通过原位恢复肺炎支原体核糖体中
Your Diffusion Model is Secretly a Zero-Shot Classifier论文阅读笔记 Rising_Flashlight 论文阅读笔记计算机视觉
YourDiffusionModelisSecretlyaZero-ShotClassifier论文阅读笔记这篇文章我感觉在智源大会上听到无数个大佬讨论，包括OpenAISora团队负责人，谢赛宁，好像还有杨植麟。虽然这个文章好像似乎被引量不是特别高，但是和AI甚至人类理解很本质的问题很相关，即是不是要通过生成来构建理解的问题，文章的做法也很巧妙，感觉是一些学者灵机一动的产物，好好学习一个！摘要这
【论文阅读】QUEEN: Query Unlearning against Model Extraction（2024） Bosenya12 科研学习模型窃取论文阅读提取攻击模型安全
摘要Modelextractionattacks（模型提取攻击）currentlyposeanon-negligiblethreat（不可忽视的威胁）tothesecurity（安全性）andprivacy（隐私性）ofdeeplearningmodels.Byqueryingthemodelwithasmalldataset（通过小数据集查询模型）andusingthequeryresultsa
【论文阅读33】Deep learning optoacoustic tomography with sparse data 弹伦琴的雷登【论文阅读系列】人工智能深度学习论文阅读图像处理
Deeplearningoptoacoustictomographywithsparsedata论文题目：基于稀疏数据的深度学习光声断层扫描论文链接：Deeplearningoptoacoustictomographywithsparsedata|NatureMachineIntelligence代码链接：GitHub-ndavoudi/sparse_artefact_unet数据链接：Data发
论文阅读瞎记(四) Cascade R-CNN: Delving into High Quality Object Detection 2017 码大哥深度学习人工智能
概述在物体检测中1，IOU阈值被用于判定正负样本。在低IOU阈值比如0.5的状态下训练模型经常产生噪音预测，然而检测效果会随着IOU增加而降低。两个主要因素：1.训练时的过拟合，正样本指数消失2.检测器最优IOU与输入假设的不匹配。一个单阶段的物体检测器CascadeR-CNN被提出用于解决这些问题。网络由一个检测序列组成，这些序列训练时会伴随IOU增长从而对FP样本更加有选择性地判别。检测器一个
【论文阅读】LLM4SGG: Large Language Models for Weakly Supervised Scene Graph Generation 进击的乔洋论文阅读语言模型人工智能计算机视觉
【论文阅读】LLM4SGG:LargeLanguageModelsforWeaklySupervisedSceneGraphGenerationabstract由于全监督方法严重依赖昂贵标注，最近弱监督场景图生成(WSSGG)研究替代方案出现。在这一点上（Inthisregard），针对WSSGG的研究主要利用图像标题（imagecaption）来获取非局部三元组，而主要关注将非局部三元组建立在图
Code Llama: Open Foundation Models for Code论文阅读 yang_daxia 大模型 llama codellama
整体介绍CodeLlama发布了3款模型，包括基础模型、Python专有模型和指令跟随模型，参数量分别为7B、13B、34B和70B。这些模型在长达16ktokens的序列上训练。都是基于Llama2。作者针对infilling(FIM)、长上下文、指令专门做了微调long-contextfine-tuning(LCFT).codellama细节CodeLlama模型家族初始化:所有CodeLla
【论文阅读】Model Stealing Attacks Against Inductive Graph Neural Networks（2021） Bosenya12 科研学习模型窃取论文阅读图神经网络模型窃取
摘要Manyreal-worlddata（真实世界的数据）comeintheformofgraphs（以图片的形式）.Graphneuralnetworks(GNNs图神经网络),anewfamilyofmachinelearning(ML)models,havebeenproposedtofullyleveragegraphdata（充分利用图数据）tobuildpowerfulapplicat
VIT论文阅读： A Image is Worth 16x16 Words Undefined游侠论文阅读
简介在2024年，大家都知道了transformer的故事，但是在4年前,CNN和Transformer谁才是CV的未来，还没有那么确定。在简介部分，作者提到了一个令人失望的事实，在基于imagenet的实验中发现，transformer的表现差于同尺寸的ResNet。作者把原因归结到biastranslationequivarianceandlocality，这些CNN具有，但是transfor
【论文阅读】GLiRA: Black-Box Membership Inference Attack via Knowledge Distillation Bosenya12 模型窃取科研学习论文阅读知识蒸馏成员推理攻击黑盒
摘要While（虽然）DeepNeuralNetworks(DNNs)havedemonstratedremarkableperformanceintasksrelatedtoperception（感知）andcontrol（控制）,therearestillseveralunresolvedconcerns（未解决的问题）regardingtheprivacyoftheirtrainingdat
【论文阅读】APMSA: Adversarial Perturbation Against Model Stealing Attacks（2023） Bosenya12 科研学习模型窃取论文阅读模型窃取防御对抗性扰动
摘要TrainingaDeepLearning(DL)model（训练深度学习模型）requiresproprietarydata（专有数据）andcomputing-intensiveresources（计算密集型资源）.Torecouptheirtrainingcosts（收回训练成本）,amodelprovidercanmonetizeDLmodelsthroughMachineLearni
Conditional Flow Matching: Simulation-Free Dynamic Optimal Transport论文阅读笔记猪猪想上树论文阅读笔记
ConditionalFlowMatching:Simulation-FreeDynamicOptimalTransport笔记发现问题连续正规化流（CNF）是一种有吸引力的生成式建模技术，但在基于模拟的最大似然训练中受到了限制。解决问题介绍一种新的条件流匹配（CFM)，一种针对CNFs的免模拟训练目标。具有稳定的回归目标，用于扩散模型中的随机流，但享有确定性流模型的有效推断。与扩散模型和CNF目
《论文阅读》EmpDG：多分辨率交互式移情对话生成 COLING 2020 365JHWZGo 情感对话论文阅读共情回复回复生成对话系统多分辨率对抗学习
《论文阅读》EmpDG：多分辨率交互式移情对话生成COLING2020前言简介模型架构共情生成器交互鉴别器损失函数前言亲身阅读感受分享，细节画图解释，再也不用担心看不懂论文啦~无抄袭，无复制，纯手工敲击键盘~今天为大家带来的是《EmpDG:Multi-resolutionInteractiveEmpatheticDialogueGeneration》出版：COLING时间：2020类型：共情回复关
安装数据库首次应用 Array_06 java oracle sql
可是为什么再一次失败之后就变成直接跳过那个要求 enter full pathname of java.exe的界面这个java.exe是你的Oracle 11g安装目录中例如：【F:\app\chen\product\11.2.0\dbhome_1\jdk\jre\bin】下的java.exe 。不是你的电脑安装的java jdk下的java.exe！注意第一次，使用SQL D
Weblogic Server Console密码修改和遗忘解决方法 bijian1013 Welogic
在工作中一同事将Weblogic的console的密码忘记了，通过网上查询资料解决，实践整理了一下。一.修改Console密码打开weblogic控制台，安全领域 --> myrealm -->&n
IllegalStateException: Cannot forward a response that is already committed Cwind java Servlets
对于初学者来说，一个常见的误解是：当调用 forward() 或者 sendRedirect() 时控制流将会自动跳出原函数。标题所示错误通常是基于此误解而引起的。示例代码： protected void doPost() { if (someCondition) { sendRedirect(); } forward(); // Thi
基于流的装饰设计模式木zi_鸣设计模式
当想要对已有类的对象进行功能增强时，可以定义一个类，将已有对象传入，基于已有的功能，并提供加强功能。自定义的类成为装饰类模仿BufferedReader，对Reader进行包装，体现装饰设计模式装饰类通常会通过构造方法接受被装饰的对象，并基于被装饰的对象功能，提供更强的功能。装饰模式比继承灵活，避免继承臃肿，降低了类与类之间的关系装饰类因为增强已有对象，具备的功能该
Linux中的uniq命令被触发 linux
Linux命令uniq的作用是过滤重复部分显示文件内容，这个命令读取输入文件，并比较相邻的行。在正常情况下，第二个及以后更多个重复行将被删去，行比较是根据所用字符集的排序序列进行的。该命令加工后的结果写到输出文件中。输入文件和输出文件必须不同。如果输入文件用“- ”表示，则从标准输入读取。 AD： uniq [选项] 文件说明：这个命令读取输入文件，并比较相邻的行。在正常情况下，第二个
正则表达式Pattern 肆无忌惮_ Pattern
正则表达式是符合一定规则的表达式，用来专门操作字符串，对字符创进行匹配，切割，替换，获取。例如，我们需要对QQ号码格式进行检验规则是长度6~12位不能0开头只能是数字，我们可以一位一位进行比较，利用parseLong进行判断，或者是用正则表达式来匹配[1-9][0-9]{4,14} 或者 [1-9]\d{4,14} &nbs
Oracle高级查询之OVER (PARTITION BY ..) 知了ing oracle sql
一、rank()/dense_rank() over(partition by ...order by ...) 现在客户有这样一个需求，查询每个部门工资最高的雇员的信息，相信有一定oracle应用知识的同学都能写出下面的SQL语句： select e.ename, e.job, e.sal, e.deptno from scott.emp e, (se
Python调试矮蛋蛋 python pdb
原文地址： http://blog.csdn.net/xuyuefei1988/article/details/19399137 1、下面网上收罗的资料初学者应该够用了，但对比IBM的Python 代码调试技巧： IBM：包括 pdb 模块、利用 PyDev 和 Eclipse 集成进行调试、PyCharm 以及 Debug 日志进行调试： http://www.ibm.com/d
webservice传递自定义对象时函数为空，以及boolean不对应的问题 alleni123 webservice
今天在客户端调用方法 NodeStatus status=iservice.getNodeStatus(). 结果NodeStatus的属性都是null。进行debug之后，发现服务器端返回的确实是有值的对象。后来发现原来是因为在客户端，NodeStatus的setter全部被我删除了。本来是因为逻辑上不需要在客户端使用setter，结果改了之后竟然不能获取带属性值的
java如何干掉指针，又如何巧妙的通过引用来操作指针————>说的就是java指针百合不是茶
C语言的强大在于可以直接操作指针的地址，通过改变指针的地址指向来达到更改地址的目的,又是由于c语言的指针过于强大，初学者很难掌握， java的出现解决了c，c++中指针的问题 java将指针封装在底层，开发人员是不能够去操作指针的地址，但是可以通过引用来间接的操作：定义一个指针p来指向a的地址（&是地址符号）：
Eclipse打不开，提示“An error has occurred.See the log file ***/.log” bijian1013 eclipse
打开eclipse工作目录的\.metadata\.log文件，发现如下错误： !ENTRY org.eclipse.osgi 4 0 2012-09-10 09:28:57.139 !MESSAGE Application error !STACK 1 java.lang.NoClassDefFoundError: org/eclipse/core/resources/IContai
spring aop实例annotation方法实现 bijian1013 java spring AOP annotation
在spring aop实例中我们通过配置xml文件来实现AOP，这里学习使用annotation来实现，使用annotation其实就是指明具体的aspect,pointcut和advice。1.申明一个切面(用一个类来实现)在这个切面里,包括了advice和pointcut AdviceMethods.jav
[Velocity一]Velocity语法基础入门 bit1129 velocity
用户和开发人员参考文档 http://velocity.apache.org/engine/releases/velocity-1.7/developer-guide.html 注释 1.行级注释## 2.多行注释#* *# 变量定义使用$开头的字符串是变量定义，例如$var1, $var2, 赋值使用#set为变量赋值，例
【Kafka十一】关于Kafka的副本管理 bit1129 kafka
1. 关于request.required.acks request.required.acks控制者Producer写请求的什么时候可以确认写成功，默认是0， 0表示即不进行确认即返回。 1表示Leader写成功即返回，此时还没有进行写数据同步到其它Follower Partition中 -1表示根据指定的最少Partition确认后才返回，这个在 Th
lua统计nginx内部变量数据 ronin47 lua nginx　统计
server { listen 80; server_name photo.domain.com; location /{set $str $uri; content_by_lua ' local url = ngx.var.uri local res = ngx.location.capture(
java-11.二叉树中节点的最大距离 bylijinnan java
import java.util.ArrayList; import java.util.List; public class MaxLenInBinTree { /* a. 1 / \ 2 3 / \ / \ 4 5 6 7 max=4 pass "root"
Netty源码学习-ReadTimeoutHandler bylijinnan java netty
ReadTimeoutHandler的实现思路：开启一个定时任务，如果在指定时间内没有接收到消息，则抛出ReadTimeoutException 这个异常的捕获，在开发中，交给跟在ReadTimeoutHandler后面的ChannelHandler，例如 private final ChannelHandler timeoutHandler = new ReadTim
jquery验证上传文件样式及大小(好用) cngolon 文件上传 jquery验证
<!DOCTYPE html> <html> <head> <meta http-equiv="Content-Type" content="text/html; charset=utf-8" /> <script src="jquery1.8/jquery-1.8.0.
浏览器兼容【转】 cuishikuan css 浏览器 IE
浏览器兼容问题一：不同浏览器的标签默认的外补丁和内补丁不同问题症状：随便写几个标签，不加样式控制的情况下，各自的margin 和padding差异较大。碰到频率:100% 解决方案：CSS里 *{margin:0;padding:0;} 备注：这个是最常见的也是最易解决的一个浏览器兼容性问题，几乎所有的CSS文件开头都会用通配符*来设
Shell特殊变量：Shell $0, $#, $*, $@, $?, $$和命令行参数 daizj shell $#$?特殊变量
前面已经讲到，变量名只能包含数字、字母和下划线，因为某些包含其他字符的变量有特殊含义，这样的变量被称为特殊变量。例如，$ 表示当前Shell进程的ID，即pid，看下面的代码： $echo $$ 运行结果 29949 特殊变量列表变量含义 $0 当前脚本的文件名 $n 传递给脚本或函数的参数。n 是一个数字，表示第几个参数。例如，第一个
程序设计KISS 原则-------KEEP IT SIMPLE, STUPID! dcj3sjt126com unix
翻到一本书，讲到编程一般原则是kiss：Keep It Simple, Stupid.对这个原则深有体会，其实不仅编程如此，而且系统架构也是如此。 KEEP IT SIMPLE, STUPID! 编写只做一件事情，并且要做好的程序；编写可以在一起工作的程序，编写处理文本流的程序，因为这是通用的接口。这就是UNIX哲学.所有的哲学真正的浓缩为一个铁一样的定律，高明的工程师的神圣的“KISS 原
android Activity间List传值 dcj3sjt126com Activity
第一个Activity： import java.util.ArrayList;import java.util.HashMap;import java.util.List;import java.util.Map;import android.app.Activity;import android.content.Intent;import android.os.Bundle;import a
tomcat 设置java虚拟机内存 eksliang tomcat 内存设置
转载请出自出处：http://eksliang.iteye.com/blog/2117772 http://eksliang.iteye.com/ 常见的内存溢出有以下两种: java.lang.OutOfMemoryError: PermGen space java.lang.OutOfMemoryError: Java heap space ------------
Android 数据库事务处理 gqdy365 android
使用SQLiteDatabase的beginTransaction()方法可以开启一个事务，程序执行到endTransaction() 方法时会检查事务的标志是否为成功，如果程序执行到endTransaction()之前调用了setTransactionSuccessful() 方法设置事务的标志为成功则提交事务，如果没有调用setTransactionSuccessful() 方法则回滚事务。事
Java 打开浏览器 hw1287789687 打开网址 open浏览器 open browser 打开url 打开浏览器
使用java 语言如何打开浏览器呢? 我们先研究下在cmd窗口中,如何打开网址使用IE 打开 D:\software\bin>cmd /c start iexplore http://hw1287789687.iteye.com/blog/2153709 使用火狐打开 D:\software\bin>cmd /c start firefox http://hw1287789
ReplaceGoogleCDN：将 Google CDN 替换为国内的 Chrome 插件 justjavac chrome Google google api chrome插件
Chrome Web Store 安装地址： https://chrome.google.com/webstore/detail/replace-google-cdn/kpampjmfiopfpkkepbllemkibefkiice 由于众所周知的原因，只需替换一个域名就可以继续使用Google提供的前端公共库了。同样，通过script标记引用这些资源，让网站访问速度瞬间提速吧
进程VS.线程 m635674608 线程
资料来源： http://www.liaoxuefeng.com/wiki/001374738125095c955c1e6d8bb493182103fac9270762a000/001397567993007df355a3394da48f0bf14960f0c78753f000 1、Apache最早就是采用多进程模式 2、IIS服务器默认采用多线程模式 3、多进程优缺点优点：多进程模式最大
Linux下安装MemCached 字符串 memcached
前提准备：1. MemCached目前最新版本为：1.4.22，可以从官网下载到。2. MemCached依赖libevent，因此在安装MemCached之前需要先安装libevent。2.1 运行下面命令，查看系统是否已安装libevent。[root@SecurityCheck ~]# rpm -qa|grep libevent libevent-headers-1.4.13-4.el6.n
java设计模式之--jdk动态代理（实现aop编程） Supanccy2013 java DAO 设计模式 AOP
与静态代理类对照的是动态代理类，动态代理类的字节码在程序运行时由Java反射机制动态生成，无需程序员手工编写它的源代码。动态代理类不仅简化了编程工作，而且提高了软件系统的可扩展性，因为Java 反射机制可以生成任意类型的动态代理类。java.lang.reflect 包中的Proxy类和InvocationHandler 接口提供了生成动态代理类的能力。 &
Spring 4.2新特性-对java8默认方法(default method)定义Bean的支持 wiselyman spring 4
2.1 默认方法(default method) java8引入了一个default medthod; 用来扩展已有的接口,在对已有接口的使用不产生任何影响的情况下,添加扩展使用default关键字 Spring 4.2支持加载在默认方法里声明的bean 2.2 将要被声明成bean的类 public class DemoService {