论文笔记及Pytorch复现:A Dual-Stage Attention-Based Recurrent Neural Network for Time Series Prediction
论文地址
GitHub代码地址
论文题目为《基于双阶段注意力机制的循环神经网络》,文章本质上还是基于Seq2Seq的模型,结合了注意力机制实现的时间序列的预测方法,文章的一大亮点是:不仅在解码器的输入阶段引入注意力机制,还在编码器阶段引入注意力机制,编码器的阶段的注意力机制实现了特征选取和把握时序依赖关系的作用。
分为两个阶段:
- 第一阶段:使用注意力机制从而能够自适应提取每个时刻的特征,这是本文的最大亮点
- 第二阶段:使用注意力机制选取与之相关的encoder hidden states
1:模型架构图
算法实现流程:
- 编码器阶段,也就是输入阶段,利用Attention机制,即:原始 x t = ( x t 1 , x t 2 , … , x t n ) {\boldsymbol{x}}_{t}=\left( x_{t}^{1}, x_{t}^{2}, \ldots, x_{t}^{n}\right) xt=(xt1,xt2,…,xtn) 利用Attention机制,结合隐层信息,会对每一维特征赋予一定的权重,转变为: x ~ t = ( α t 1 x t 1 , α t 2 x t 2 , … , α t n x t n ) \tilde{\boldsymbol{x}}_{t}=\left(\alpha_{t}^{1} x_{t}^{1}, \alpha_{t}^{2} x_{t}^{2}, \ldots, \alpha_{t}^{n} x_{t}^{n}\right) x~t=(αt1xt1,αt2xt2,…,αtnxtn),从而实现自适应提取每个时刻的各个维度特征,使用更新后的 x ~ t \tilde{\boldsymbol{x}}_{t} x~t 作为编码器的输入。这也是本篇文章最大的亮点!
- 解码器阶段,也就是输出阶段,与传统Attention实现功能相同,使用另一个注意力机制选取与之相关的encoder hidden states
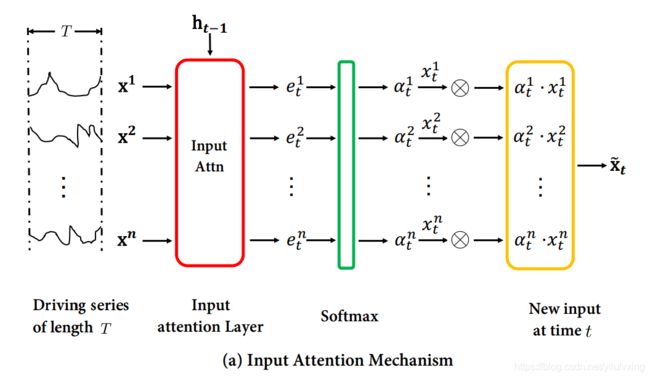
2:输入阶段的Attention
第一阶段输入阶段的编码器Attention机制实现过程如下:
文章中定义 h t ∈ R m \mathbf{h}_{t} \in \mathbb{R}^{m} ht∈Rm 为encoder在时刻 t t t 的hidden state, 其中 m m m 是hidden state的大小。
第一阶段,使用当前时刻的输人 x t ∈ R n , \boldsymbol{x}_{t} \in \mathbb{R}^{n}, xt∈Rn, 以及上一个时刻编码器的hidden state h t − 1 \boldsymbol{h}_{\boldsymbol{t}-1} ht−1, 来计算当前时刻编码器的hidden state h t ∈ R m , \boldsymbol{h}_{t} \in \mathbb{R}^{m}, ht∈Rm, 其中m是编码器的size。更新公式可写为:
h t = f 1 ( h t − 1 , x t ) h_{t}=f_{1}\left(h_{t-1}, \boldsymbol{x}_{t}\right) ht=f1(ht−1,xt)
其中 f 1 f_{1} f1是一个非线性激活函数,我们可以使用通常的循环神经网络vanilla RNN或LSTM以及GRU作为 f 1 f_{1} f1 ,在该文章中,使用的是LSTM来捕获长依赖关系。
这里,为了自适应地选取相关feature(即给每一个特征赋予一定的权重), 作者在此处引入了注意力机制。简单来说,即对每个时刻的输入 x t \boldsymbol{x}_{t} xt 为其中的每个影响因子赋予一定的注意力权重(attention weight) α t k \alpha_{t}^{k} αtk 。 α t k \alpha_{t}^{k} αtk 衡量了时刻 t t t 的第 k k k 个 feature的重要性。更新后的 x ~ t \tilde{\boldsymbol{x}}_{t} x~t 为
x ~ t = ( α t 1 x t 1 , α t 2 x t 2 , … , α t n x t n ) \tilde{\boldsymbol{x}}_{t}=\left(\alpha_{t}^{1} x_{t}^{1}, \alpha_{t}^{2} x_{t}^{2}, \ldots, \alpha_{t}^{n} x_{t}^{n}\right) x~t=(αt1xt1,αt2xt2,…,αtnxtn)
那么 α t k \alpha_{t}^{k} αtk 如何计算得到?
文章中给出的方法:根据上一个时刻编码器的hidden state h t − 1 \boldsymbol{h}_{\boldsymbol{t}-\mathbf{1}} ht−1 和cell state s t − 1 \boldsymbol{s}_{\boldsymbol{t}-\mathbf{1}} st−1 计算得到:
e t k = v e T tanh ( W e [ h t − 1 ; s t − 1 ] + U e x k ) e_{t}^{k}=\boldsymbol{v}_{e}^{T} \tanh \left(\boldsymbol{W}_{e}\left[\boldsymbol{h}_{t-1} ; \boldsymbol{s}_{t-1}\right]+\boldsymbol{U}_{e} \boldsymbol{x}^{k}\right) etk=veTtanh(We[ht−1;st−1]+Uexk)
其中 [ h t − 1 ; s t − 1 ] \left[\boldsymbol{h}_{t-1} ; \boldsymbol{s}_{t-1}\right] [ht−1;st−1] 是hidden state h t − 1 \boldsymbol{h}_{t-1} ht−1 与cell state s t − 1 \boldsymbol{s}_{t-1} st−1 的连接(concatenation)。
该式即把第 k k k 个driving series(文章中的driving series就是特征的含义)与前一个时刻的hidden state h t − 1 \boldsymbol{h}_{\boldsymbol{t}-1} ht−1 和cell state s t − 1 \boldsymbol{s}_{\boldsymbol{t}-\mathbf{1}} st−1 线性组合, 再用 tanh激活得到。
计算得到 e t k e_{t}^{k} etk 后,再用softmax函数进行归一化:
α t k = exp ( e t k ) ∑ i − 1 n exp ( e t i ) \alpha_{t}^{k}=\frac{\exp \left(e_{t}^{k}\right)}{\sum_{i-1}^{n} \exp \left(e_{t}^{i}\right)} αtk=∑i−1nexp(eti)exp(etk)
更新后的 x ~ t \tilde{\boldsymbol{x}}_{t} x~t
x ~ t = ( α t 1 x t 1 , α t 2 x t 2 , … , α t n x t n ) \tilde{\boldsymbol{x}}_{t}=\left(\alpha_{t}^{1} x_{t}^{1}, \alpha_{t}^{2} x_{t}^{2}, \ldots, \alpha_{t}^{n} x_{t}^{n}\right) x~t=(αt1xt1,αt2xt2,…,αtnxtn)作为下一个阶段temporal Attention的输入
input attention机制,使得编码器能够关注其中输入特征中重要的特征,而不是对所有特征一视同仁,这也是所有attention的本质作用。
3:temporal attention的解码器
第二阶段temporal Attention机制实现过程如下:
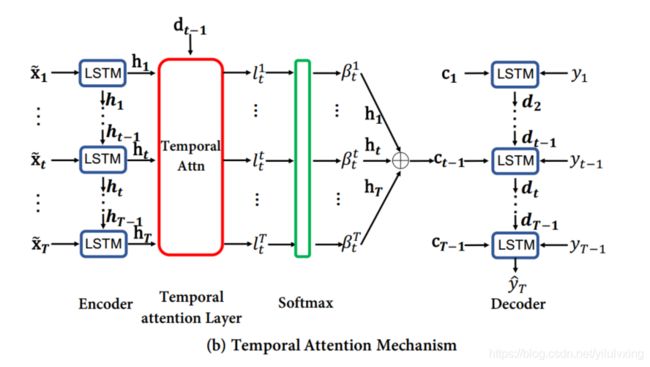
为了区别起见,参考罗未萌的建议,与论文中公式略有不同的是,将解码器中的时间序列下标标注为 t ′ , t^{\prime}, t′, 以与编码 器种的下标 t t t 区分。
第二阶段的解码器注意力机制设计类似于传统的seq2seq中的Attention机制,也就是第二阶段temporal attention的机制其实就是传统Attention的机制。
传统Attentionde 解决的问题是: 传统的seq2seq模型中, 编码器输出的context vector基于最后时刻的hidden state或对所有 hidden state取平均。这样输出的context vector对所有时刻 t t t 均相同,没有体现出差异化,就像人一样没有将注意力集中到关键部分,无法起到只选取相关时刻编码器hidden state的功能。
解决问题的思路是在不同时刻采用不同的context vector。类似于 seq2seq, 最简单的办法是对所有时刻的 h t ′ \boldsymbol{h}_{t^{\prime}} ht′ 取加权平均, 即:
c t ′ = ∑ t = 1 T β t ′ t h t \boldsymbol{c}_{t^{\prime}}=\sum_{t=1}^{T} \beta_{t^{\prime}}^{t} h_{t} ct′=t=1∑Tβt′tht
β t ′ t \beta_{t^{\prime}}^{t} βt′t 是基于前一个时刻解码器的hidden state d t ′ − 1 \boldsymbol{d}_{\boldsymbol{t}^{\prime}-\mathbf{1}} dt′−1 和cell state s t ′ − 1 ′ s_{t^{\prime}-1}^{\prime} st′−1′ 计算得到:
l t ′ t = v d T tanh ( W d [ d t ′ − 1 ; s t ′ − 1 ′ ] + U d h t ) l_{t^{\prime}}^{t}=\boldsymbol{v}_{d}^{T} \tanh \left(\boldsymbol{W}_{d}\left[\boldsymbol{d}_{t^{\prime}-1} ; \boldsymbol{s}_{t^{\prime}-1}^{\prime}\right]+\boldsymbol{U}_{d} \boldsymbol{h}_{t}\right) lt′t=vdTtanh(Wd[dt′−1;st′−1′]+Udht)
β t ′ t = exp ( l t ′ t ) ∑ j = 1 T exp ( l t ′ j ) \beta_{t^{\prime}}^{t}=\frac{\exp \left(l_{t^{\prime}}^{t}\right)}{\sum_{j=1}^{T} \exp \left(l_{t^{\prime}}^{j}\right)} βt′t=∑j=1Texp(lt′j)exp(lt′t)
根据文章中的模型流程,可以看到解码器的输入是上一个时刻的目标序列 y t ′ − 1 y_{t^{\prime}-1} yt′−1 和hidden state d t ′ − 1 \boldsymbol{d}_{t^{\prime}-1} dt′−1 以及context vector c t ′ − 1 \boldsymbol{c}_{t^{\prime}-1} ct′−1共同组成
即 d t ′ = f 2 ( y t ′ − 1 , c t ′ − 1 , d t ′ − 1 ) \boldsymbol{d}_{t^{\prime}}=f_{2}\left(y_{t^{\prime}-1}, \boldsymbol{c}_{t^{\prime}-1}, \boldsymbol{d}_{t^{\prime}-1}\right) dt′=f2(yt′−1,ct′−1,dt′−1)
然后
d t ′ = f 2 ( d t ′ − 1 , y ~ t ′ − 1 ) \boldsymbol{d}_{t^{\prime}}=f_{2}\left(\boldsymbol{d}_{t^{\prime}-1}, \tilde{y}_{t^{\prime}-1}\right) dt′=f2(dt′−1,y~t′−1)
类似于编码器的最后一个公式, 这里的激活函数 f 2 f_{2} f2 还是选择LSTM。
4:预测部分
文章回顾了非线性自回归(Nonlinear autoregressive exogenous, NARX)模型的最终目标,需要建立当前输入与所有时刻的输人以及之前时刻的输出之间的关系,即:
y ^ T = F ( y 1 , … , y T − 1 , x 1 , … , x T ) \hat{y}_{T}=F\left(y_{1}, \ldots, y_{T-1}, \boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{T}\right) y^T=F(y1,…,yT−1,x1,…,xT)
通过之前编码器解码器模型的训练,已经得到了解码器的hidden state 和context vector, h T \boldsymbol{h}_{T} hT 与 c T \boldsymbol{c}_{T} cT 。最后再使用一个全连接层对 y ^ T \hat{y}_{T} y^T 做回归, 即
y ^ T = v y T ( W y [ d T ; c T ] + b w ) + b v \hat{y}_{T}=\boldsymbol{v}_{y}^{T}\left(\boldsymbol{W}_{y}\left[\boldsymbol{d}_{T} ; \boldsymbol{c}_{T}\right]+\boldsymbol{b}_{w}\right)+b_{v} y^T=vyT(Wy[dT;cT]+bw)+bv
这样可以得到最终的预测 y ^ \hat{y} y^
5:总结
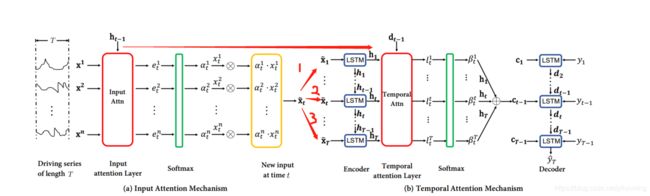
文章是将input Attention 和temporal Attention 分开讲述的,模型架构图是放在一起的,刚开始读完论文些不太理解的地方:
如input attention 中的f1是使用LSTM,接着 x ~ t \tilde{\mathbf{x}}_{t} x~t又作为temporal Attention 中LSTM的输入,接着解码层,又使用LSTM来进行预测,这样的话,不就是共有3个LSTM进行训练吗?
在深入阅读以及查看源代码后,发现之前理解出现偏差,其实总共只有2个阶段LSTM,分别对应input attention阶段用来提取自适应特征的attention模块中的LSTM,解码阶段的LSTM。我重新模型架构图整理了下,并进行箭头标注,表示对应的位置。
左边 input attention一大块计算得到的 x ~ t \tilde{\mathbf{x}}_{t} x~t, x ~ t \tilde{\boldsymbol{x}}_{t} x~t x ~ t = ( α t 1 x t 1 , α t 2 x t 2 , … , α t n x t n ) \tilde{\boldsymbol{x}}_{t}=\left(\alpha_{t}^{1} x_{t}^{1}, \alpha_{t}^{2} x_{t}^{2}, \ldots, \alpha_{t}^{n} x_{t}^{n}\right) x~t=(αt1xt1,αt2xt2,…,αtnxtn)
实际上只是temporal attention中的一个时刻的输入, 我们从input attention h t \mathbf{h}_{t} ht的与temporal attention中的 h t \mathbf{h}_{t} ht对应的位置可以观察到。
也就是说,坐标的input attention 实际上只是temporal attention将某一个时刻剥离出来的计算过程细节而已。单看右边的temporal attention,实际上就是一个Seq2Seq的attention的实现,并没有不同,作者将temporal attention的输入 x ~ t \tilde{\mathbf{x}}_{t} x~t单独剥离出来,强调其计算过程,也就是input attention的实现机制,目的就是说明文章的亮点:在输入阶段也实现基于attention的自适应特征的提取
6: 数据输入部分
原始数据大小:[110,81]
训练数据比例:70%
默认批数据量大小:128
train_timesteps:110*0.7=77
时间窗口长度:T=10
因此第一批训练数据长度为:67 = ref_idx = np.array(range(self.train_timesteps - self.T))
下面以第一批训练数据为例:
原始数据X维度:[67,81]
Encoder层:
X_tilde 的初始化为0:[67,9,81]
LSTM的隐层h_n和输出层s_n的初始化:[1,67,64]
h_n、s_n经过repeat得到[67, 81, 9]
然后经过torch.cat将h_n、s_n和X_tilde进行拼接,得到x:[67, 81, 137]
经过view函数进行维度重塑,得到# [5427, 137]
再经过attention层,得到x:[5427, 1]
再经过view函数进行维度重塑并且维度reshape得到alpha,即每个特征的权重大小alpha:[67,81]
通过unsqueeze函数进行维度变化得到[1, 67, 81],并将其作为LSTM的输入,输入格式为:
self.encoder_lstm(x_tilde.unsqueeze(0), (h_n, s_n))
并将隐层和输入层进行赋值,作为下一个T时刻的输入
h_n = final_state[0] # [1, 67, 64]
s_n = final_state[1] # [1, 67, 64
X_tilde[:, t, :] = x_tilde # X_tilde[:, t, :] [67, 81] Encoder层中的LSTM中的输入 (带有权重的输入)
X_encoded[:, t, :] = h_n # X_encoded[:, t, :] [67, 64] Encoder层中的LSTM中的隐层输出 (经过LSTM后的输出)
Encoder层返回的是[67, 9, 64]
Decoder层:
输入数据X_encoded:[67, 9, 64]
输入数据y: y_prev:[67, 9] 作为前一时刻的输出结果与当前进行拼接
LSTM的隐层d_n和输出层c_n的初始化: [1, 67, 128]
d_n、c_n经过repeat得到[67, 9, 64]
然后经过torch.cat将d_n、c_n和X_encoded进行拼接,得到x:[67, 9, 320]
经过view函数进行维度重塑,得到 [603, 320]
再经过attention层,得到x:[603, 1]
再经过view函数进行维度重塑并且softmax得到beta,得到 # [67,1,9] 即向量的权重
通过unsqueeze函数进行维度变化得到[67,1,9]
通过torch.bmm(beta.unsqueeze(1), X_encoded)进行矩阵相乘得到[67,1,64],经过变换得到context [67, 64]
最后将context与上一个时刻y_prev[:, t]进行全连接得到y_tilde [67, 1]
将其作为LSTM的输入, self.lstm_layer(y_tilde.unsqueeze(0), (d_n, c_n))
d_n = final_states[0] # 1 * batch_size * decoder_num_hidden
c_n = final_states[1] # 1 * batch_size * decoder_num_hidden
最后LSTM的输出
7:关键部分代码
import matplotlib.pyplot as plt
import torch
import numpy as np
from torch import nn
from torch import optim
from torch.autograd import Variable
import torch.nn.functional as F
class Encoder(nn.Module):
"""encoder in DA_RNN."""
def __init__(self, T,
input_size,
encoder_num_hidden,
parallel=False):
"""Initialize an encoder in DA_RNN."""
super(Encoder, self).__init__()
self.encoder_num_hidden = encoder_num_hidden
self.input_size = input_size
self.parallel = parallel
self.T = T
# Fig 1. Temporal Attention Mechanism: Encoder is LSTM
self.encoder_lstm = nn.LSTM(
input_size=self.input_size,
hidden_size=self.encoder_num_hidden,
num_layers=1
)
# Construct Input Attention Mechanism via deterministic attention model
# Eq. 8: W_e[h_{t-1}; s_{t-1}] + U_e * x^k
self.encoder_attn = nn.Linear(
in_features=2 * self.encoder_num_hidden + self.T - 1,
out_features=1
)
def forward(self, X):
"""forward.
Args:
X: input data
"""
X_tilde = Variable(torch.zeros(X.size(0), self.T - 1,self.input_size))
print('X_tilde',X_tilde.shape) #[67, 9, 81]
X_encoded = Variable(torch.zeros(X.size(0), self.T - 1,self.encoder_num_hidden)) #[67, 9, 64]
# X_tilde = Variable(X.data.new(
# X.size(0), self.T - 1, self.input_size).zero_())
# X_encoded = Variable(X.data.new(
# X.size(0), self.T - 1, self.encoder_num_hidden).zero_())
# Eq. 8, parameters not in nn.Linear but to be learnt
# v_e = torch.nn.Parameter(data=torch.empty(
# self.input_size, self.T).uniform_(0, 1), requires_grad=True)
# U_e = torch.nn.Parameter(data=torch.empty(
# self.T, self.T).uniform_(0, 1), requires_grad=True)
# h_n, s_n: initial states with dimention hidden_size
h_n = self._init_states(X) # 初始化LSTM hidden信息
s_n = self._init_states(X) # 初始化LSTM cell信息
print('initial-h_n',h_n.shape) # [1, 67, 64] # 输入信息self.num_layers,x.size(0), self.hidden_size)
print('initial-h_n',s_n.shape) # [1, 67, 64] # 输入信息self.num_layers,x.size(0), self.hidden_size)
'''
nhidden_encoder = 64
batchsize = 200
'''
# 输入的X :[67, 9, 81]
# Encoder层的for循环的作用:计算attention的权重后,将数据输入至Encoder层的LSTM进行训练,共T-1次
for t in range(self.T - 1):
print('-----AAA--------')
print('X_tilde', X_tilde.shape) # [67, 9, 81]
# batch_size * input_size * (2 * hidden_size + T - 1)
print('h_n.repeat',h_n.repeat(self.input_size, 1, 1).permute(1, 0, 2).shape) #[67, 81, 64]
print('s_n.repeat',s_n.repeat(self.input_size, 1, 1).permute(1, 0, 2).shape) #[67, 81, 64]
print('X.permute',X.permute(0, 2, 1).shape) #[67, 81, 9]
x = torch.cat((h_n.repeat(self.input_size, 1, 1).permute(1, 0, 2),
s_n.repeat(self.input_size, 1, 1).permute(1, 0, 2),
X.permute(0, 2, 1)), dim=2)
print('x',x.shape) #[67, 81, 137]
print('x.view',(x.view(-1, self.encoder_num_hidden * 2 + self.T - 1)).shape) # [5427, 137]
x = self.encoder_attn(
x.view(-1, self.encoder_num_hidden * 2 + self.T - 1))
print('x-shape',x.shape) # [5427, 1]
# get weights by softmax
alpha = F.softmax(x.view(-1, self.input_size))
print('alpha',alpha.shape) # [67, 81]
# get new input for LSTM
print(' X[:, t, :]', X[:, t, :].shape) #[67, 81]
x_tilde = torch.mul(alpha, X[:, t, :])
print('x_tilde',x_tilde.shape) # [67, 81]
# Fix the warning about non-contiguous memory
# https://discuss.pytorch.org/t/dataparallel-issue-with-flatten-parameter/8282
self.encoder_lstm.flatten_parameters() ## 这段代码的含义是什么? 有什么作用?
# 输入信息self.num_layers,x.size(0), self.hidden_size)
print('x_tilde.unsqueeze(0)',x_tilde.unsqueeze(0).shape) #[1, 67, 81] 作为LSTM的输入数据
# encoder LSTM
_, final_state = self.encoder_lstm(
x_tilde.unsqueeze(0), (h_n, s_n))
print('final_state[0]',final_state[0].shape) # [1, 67, 64]
h_n = final_state[0] # [1, 67, 64]
s_n = final_state[1] # [1, 67, 64]
X_tilde[:, t, :] = x_tilde # X_tilde[:, t, :] [67, 81] Encoder层中的LSTM中的输入
X_encoded[:, t, :] = h_n # X_encoded[:, t, :] [67, 64] Encoder层中的LSTM中的隐层输出
return X_tilde, X_encoded
def _init_states(self, X):
"""Initialize all 0 hidden states and cell states for encoder."""
# https://pytorch.org/docs/master/nn.html?#lstm
return Variable(X.data.new(1, X.size(0), self.encoder_num_hidden).zero_())
class Decoder(nn.Module):
"""decoder in DA_RNN."""
def __init__(self, T, decoder_num_hidden, encoder_num_hidden):
"""Initialize a decoder in DA_RNN."""
super(Decoder, self).__init__()
self.decoder_num_hidden = decoder_num_hidden
self.encoder_num_hidden = encoder_num_hidden
self.T = T
self.attn_layer = nn.Sequential(
nn.Linear(2 * decoder_num_hidden +
encoder_num_hidden, encoder_num_hidden),
nn.Tanh(),
nn.Linear(encoder_num_hidden, 1)
)
self.lstm_layer = nn.LSTM(
input_size=1,
hidden_size=decoder_num_hidden
)
self.fc = nn.Linear(encoder_num_hidden + 1, 1)
self.fc_final = nn.Linear(decoder_num_hidden + encoder_num_hidden, 1)
self.fc.weight.data.normal_()
def forward(self, X_encoded, y_prev):
print('-----BBB--------')
print('X_encoded',X_encoded.shape) # [67, 9, 64]
print('y_prev',y_prev.shape) # [67, 9]
"""forward."""
d_n = self._init_states(X_encoded) # 初始化LSTM hidden信息
c_n = self._init_states(X_encoded) # 初始化LSTM cell信息
print('initial-d_n',d_n.shape) # [1, 67, 128] # 输入信息self.num_layers,x.size(0), self.hidden_size)
print('initial-c_n',c_n.shape) # [1, 67, 128]
# Decoder 层的for循环作用:将Encoder层的计算结果输入至Decoder层的Attention层进行计算
# 得到权重,权重Beta再和Encoder中输入h1(h1即X_encoded)计算矩阵乘积,得到context,再将context输入至Decoder层的LSTM
# 并与上一次LSTM中的输出结果进行cat,计算T-1次,即LSTM的时间戳长度
for t in range(self.T - 1):
print('d_n.repeat', d_n.repeat(self.T - 1, 1, 1).permute(1, 0, 2).shape) # [67, 9, 128]
print('c_n.repeat',c_n.repeat(self.T - 1, 1, 1).permute(1, 0, 2).shape) # [67, 9, 128]
print('X_encoded',X_encoded.shape) # [67, 9, 64]
x = torch.cat((d_n.repeat(self.T - 1, 1, 1).permute(1, 0, 2),
c_n.repeat(self.T - 1, 1, 1).permute(1, 0, 2),
X_encoded), dim=2)
print('x-shape',x.shape) # [67, 9, 320]
print('x.view',x.view(-1, 2 * self.decoder_num_hidden + self.encoder_num_hidden).shape) # [603, 320]
x = self.attn_layer(
x.view(-1, 2 * self.decoder_num_hidden + self.encoder_num_hidden))
print('x-atten',x.shape) # [603, 1])
beta = F.softmax(x.view(-1, self.T - 1))
print('beta',beta.shape) # [67, 9] 得到权重
# Eqn. 14: compute context vector
# batch_size * encoder_hidden_size
print('beta.unsqueeze(1)',beta.unsqueeze(1).shape) # [67,1,9] # X_encoded [67, 9, 64] 矩阵相乘得到 [67,1,64]
print('torch.bmm(beta.unsqueeze(1), X_encoded)',torch.bmm(beta.unsqueeze(1), X_encoded).shape) # [67,1,64]
context = torch.bmm(beta.unsqueeze(1), X_encoded)[:, 0, :]
print('context',context.shape) # [67, 64]
if t < self.T - 1:
# Eqn. 15
# batch_size * 1
print('y_prev[:, t].unsqueeze(1)',y_prev[:, t].unsqueeze(1).shape) # [67, 1]
y_tilde = self.fc(
torch.cat((context, y_prev[:, t].unsqueeze(1)), dim=1)) # 上一个时刻的预测值与当前隐层进行拼接
print('y_tilde',y_tilde.shape) # [67, 1])
# Eqn. 16: LSTM
self.lstm_layer.flatten_parameters()
_, final_states = self.lstm_layer(
y_tilde.unsqueeze(0), (d_n, c_n))
d_n = final_states[0] # 1 * batch_size * decoder_num_hidden
c_n = final_states[1] # 1 * batch_size * decoder_num_hidden
# final_states[0] torch.Size([1, 67, 128])
# final_states[1] torch.Size([1, 67, 128])
# Eqn. 22: final output
print('d_n[0]',d_n[0].shape) #[67, 128]
y_pred = self.fc_final(torch.cat((d_n[0], context), dim=1)) # 将LSTM最后一个cell的输出与attention的输入进行拼接,然后输出结果
# y_pred [67, 1]
return y_pred
def _init_states(self, X):
"""Initialize all 0 hidden states and cell states for encoder."""
# hidden state and cell state [num_layers*num_directions, batch_size, hidden_size]
# https://pytorch.org/docs/master/nn.html?#lstm
return Variable(X.data.new(1, X.size(0), self.decoder_num_hidden).zero_())
class DA_RNN(nn.Module):
"""Dual-Stage Attention-Based Recurrent Neural Network."""
def __init__(self, X, y, T,
encoder_num_hidden,
decoder_num_hidden,
batch_size,
learning_rate,
epochs,
parallel=False):
"""initialization."""
super(DA_RNN, self).__init__()
self.encoder_num_hidden = encoder_num_hidden
self.decoder_num_hidden = decoder_num_hidden
self.learning_rate = learning_rate
self.batch_size = batch_size
self.parallel = parallel
self.shuffle = False
self.epochs = epochs
self.T = T
self.X = X
self.y = y
self.device = torch.device(
'cuda:0' if torch.cuda.is_available() else 'cpu')
print("==> Use accelerator: ", self.device)
self.Encoder = Encoder(input_size=X.shape[1],
encoder_num_hidden=encoder_num_hidden,
T=T).to(self.device)
self.Decoder = Decoder(encoder_num_hidden=encoder_num_hidden,
decoder_num_hidden=decoder_num_hidden,
T=T).to(self.device)
# Loss function
self.criterion = nn.MSELoss()
if self.parallel:
self.encoder = nn.DataParallel(self.encoder)
self.decoder = nn.DataParallel(self.decoder)
self.encoder_optimizer = optim.Adam(params=filter(lambda p: p.requires_grad,
self.Encoder.parameters()),
lr=self.learning_rate)
self.decoder_optimizer = optim.Adam(params=filter(lambda p: p.requires_grad,
self.Decoder.parameters()),
lr=self.learning_rate)
# Training set
self.train_timesteps = int(self.X.shape[0] * 0.7) # 原始数据csv共110条数据,因此train_timesteps=77
self.y = self.y - np.mean(self.y[:self.train_timesteps])
self.input_size = self.X.shape[1]
def train(self):
"""Training process."""
iter_per_epoch = int(
np.ceil(self.train_timesteps * 1. / self.batch_size))
self.iter_losses = np.zeros(self.epochs * iter_per_epoch)
self.epoch_losses = np.zeros(self.epochs)
n_iter = 0
for epoch in range(self.epochs):
# ref_idx长度大小=77-10=67
# ref_idx:67
if self.shuffle:
ref_idx = np.random.permutation(self.train_timesteps - self.T) # 打乱顺序排序
else:
ref_idx = np.array(range(self.train_timesteps - self.T)) # 按顺序输出 数据长度- 时间戳长度
idx = 0
# 按batch_size(64条)进行处理,直到达到train_timesteps数据量,首先是0<77,然后是64<77
while (idx < self.train_timesteps):
# get the indices of X_train
# batch_size=128,大于idx长度,所以indices即为整个ref_idx的索引,长度为67
indices = ref_idx[idx:(idx + self.batch_size)]
# x = np.zeros((self.T - 1, len(indices), self.input_size))
x = np.zeros((len(indices), self.T - 1, self.input_size)) # x:[64,9,81]
y_prev = np.zeros((len(indices), self.T - 1)) # y_prev:[64,9] 训练的y_prev
y_gt = self.y[indices + self.T] # y_gt:indices 后的第T个真实y值与预测进行比较 因此长度也为67
# format x into 3D tensor 数据切分,X和y
for bs in range(len(indices)): # range: 0-67
x[bs, :, :] = self.X[indices[bs]:(indices[bs] + self.T - 1), :] # 赋值数据,原始数据每次[9,81]赋予 x
y_prev[bs, :] = self.y[indices[bs]: (indices[bs] + self.T - 1)] # 原始y值每次赋予9个数值给y_prev
loss = self.train_forward(x, y_prev, y_gt) # 输入训练数据,真实值和预测值进行比较
self.iter_losses[int(
epoch * iter_per_epoch + idx / self.batch_size)] = loss
idx += self.batch_size
n_iter += 1
if n_iter % 10000 == 0 and n_iter != 0:
for param_group in self.encoder_optimizer.param_groups:
param_group['lr'] = param_group['lr'] * 0.9
for param_group in self.decoder_optimizer.param_groups:
param_group['lr'] = param_group['lr'] * 0.9
self.epoch_losses[epoch] = np.mean(self.iter_losses[range(
epoch * iter_per_epoch, (epoch + 1) * iter_per_epoch)])
if epoch % 10 == 0:
print("Epochs: ", epoch, " Iterations: ", n_iter,
" Loss: ", self.epoch_losses[epoch])
if epoch % 10 == 0:
y_train_pred = self.test(on_train=True)
y_test_pred = self.test(on_train=False)
y_pred = np.concatenate((y_train_pred, y_test_pred))
plt.ioff()
plt.figure()
plt.plot(range(1, 1 + len(self.y)), self.y, label="True")
plt.plot(range(self.T, len(y_train_pred) + self.T),
y_train_pred, label='Predicted - Train')
plt.plot(range(self.T + len(y_train_pred), len(self.y) + 1),
y_test_pred, label='Predicted - Test')
plt.legend(loc='upper left')
plt.show()
def train_forward(self, X, y_prev, y_gt): #训练数据
"""Forward pass."""
# zero gradients
self.encoder_optimizer.zero_grad() # 初始化
self.decoder_optimizer.zero_grad()
# 编码器
input_weighted, input_encoded = self.Encoder(
Variable(torch.from_numpy(X).type(torch.FloatTensor).to(self.device)))
# 解码器
y_pred = self.Decoder(input_encoded, Variable(
torch.from_numpy(y_prev).type(torch.FloatTensor).to(self.device)))
y_true = Variable(torch.from_numpy(
y_gt).type(torch.FloatTensor).to(self.device))
y_true = y_true.view(-1, 1)
loss = self.criterion(y_pred, y_true)
loss.backward()
self.encoder_optimizer.step()
self.decoder_optimizer.step()
return loss.item()