层次聚类详解(附代码)

本篇博客主要介绍机器学习算法中的层次聚类，层次聚类不同于传统的K-Means聚类算法，它在初始K值和初始聚类中心点的选择问题上会存在优势。 

层次聚类

层次聚类就是一层一层的进行聚类，可以由下向上，或由上向下进行聚类。先计算样本之间的距离，每次将距离最近的点合并到同一个类。然后，再计算类与类之间的距离，将距离最近的类合并为一个大类。不停的合并，直到合成了一个类。其中类与类的距离的计算方法有：最短距离法，最长距离法，中间距离法，类平均法等。

层次分解顺序为：自下向上和自上向下两种，即凝聚的层次聚类算法和分裂的层次聚类算法，这两种方法没有优劣之分，只是在实际应用的过程中根据数据的特点以及想得到的类，来考虑具体那种方法计算时所花费的时间少，数据不同时间也会相应的不同。

层次聚类的流程

凝聚型层次聚类的策略是先将每个对象作为一个簇，然后合并这些原子簇为越来越大的簇，直到所有对象都在一个簇中，或者某个终结条件被满足。绝大多数层次聚类属于凝聚型层次聚类，它们只是在簇间相似度的定义上有所不同。这里给出采用最小距离的凝聚层次聚类算法流程：

1. 将每个对象看作一类，计算两两之间的最小距离；
2. 将距离最小的两个类合并成一个新类；
3. 重新计算新类与所有类之间的距离；
4. 重复2、3，直到所有类最后合并成一类；

层次聚类的优缺点 

优点：1，距离和规则的相似度容易定义，限制少；2，不需要预先制定聚类数；3，可以发现类的层次关系；4，可以聚类成其它形状

缺点：1，计算复杂度太高；2，奇异值也能产生很大影响；3，算法很可能聚类成链状

 K值的确定

往往我们在对无target的数据进行无监督的学习时，都会用聚类算法进行学习，但是聚类算法确定K值是最重要也是最困难的，有时我们可以根据经验去确定我们的数据分成几类，但同时我们也有很多定性的方法去辅助我们具体分为几类。

1. 最常用最简单的方法可视化数据，然后观察出聚类聚成几类比较合适，但是在数据量很大时，往往很难观察；
2. 绘制出k-average with cluster distance to centroid的图表，观察随着k值的增加，曲线的下降情况，当曲线不再“急剧”下降时，就是合适的k值
3. 计算不同k值下KMeans算法的BIC和AIC值，BIC或AIC值越小，选择该k值
4. 使用轮廓系数来确定，选择使系数较大所对应的k值
5. 利用层次聚类，可视化后认为地观察认定可聚为几类，确定k值，确定较粗的数目，并找到一个初始聚类，然后用迭代重定位来改进该聚类。

通常第二种方法是我们会比较多使用到的方法，通过曲线去确定具体的K值；但经常会产生较好的聚类结果的一个有趣策略是，首先采用层次凝聚算法决定结果粗的数目，并找到一个初始聚类，然后用迭代重定位来改进该聚类。 但是在使用层次聚类时需要注意几个问题，（1）由于层次聚类的算法时间复杂度很高，所以采取随机抽样的方式去进行模型的训练，大概几千的样本数量就可以；（2）由于要进行聚类算法，所以最好对所有特征进行归一化处理；（3）如果进行归一化后还是要将所有的特征放在一起进行聚类，最好可以对每个特征进行权重的赋值，对于权重较高的特征给予高的权重，当然也可是视所有的特征权重都为1，但在实际应用中还是要根据实际情况和业务而定；

过程步骤代码参考

def gave_data(df):
    # 训练数据
    df_train = df.iloc[:,1:]
    # 随机抽取样本，从大样本中每次随机抽取小样本
    sample_df = df_train.sample(n=1000)
    # 归一化处理，对聚类数据进行归一化处理
    min_max_scaler = preprocessing.MinMaxScaler()
    X_minMax = min_max_scaler.fit_transform(sample_df)
    # 一类一标签
    # labelture = [i for i in range(sample_df.shape[0])]
    # 统一标签
    labelture = [0 for i in range(sample_df.shape[0])]
    return X_minMax, labelture

 这里我们通过pandas读取一个csv文件成DF，我们对数据进行随机抽样，此处我们只随机抽样1000条样本，再对这1000条样本进行归一化处理，这里没有对每一个特征进行权重处理，此处默认每一个特征的特征权重都为1，这里我们返回一个处理过的数据集X_minMax和数据标签label，此处默认label统一都为0。

def tree(X, labelture):
    # row_clusters = linkage(pdist(df, metric='euclidean'), method='complete')  # 使用抽秘籍距离矩阵
    row_clusters = linkage(X, method='complete', metric='euclidean')
    print (pd.DataFrame(row_clusters, columns=['row label1', 'row label2', 'distance', 'no. of items in clust.'],
                        index=['cluster %d' % (i + 1) for i in range(row_clusters.shape[0])]))

    # 层次聚类树
    row_dendr = dendrogram(row_clusters, labels=labelture)
    plt.tight_layout()
    plt.ylabel('Euclidean distance')
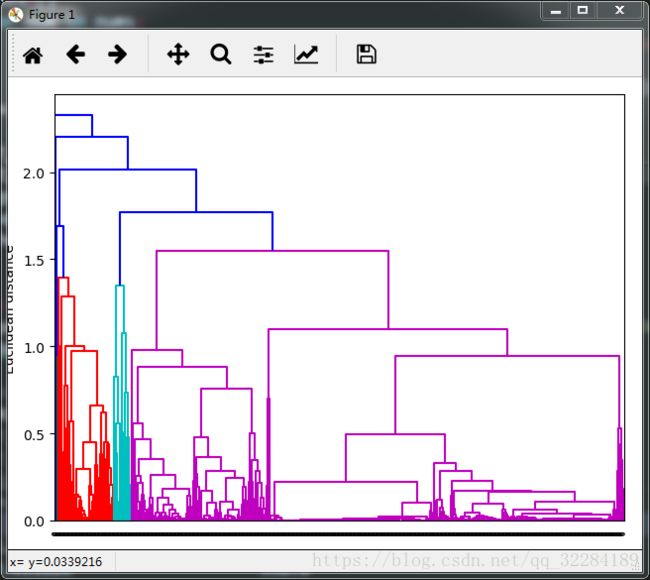
    plt.show()

这里我们通过此段代码来绘制分层树，用到的参数即为上面得到的数据集X_minMax和标签label。

通过上图的分层树可以发现，大概这1000个样本可以分为4类

所以对于整个数据集，我们第一次分类可先让K=4，进行聚类，随后迭代得到最优的K值。

def cluster_test(data):
# 传统聚类
	print "------------------------------------"
# 归一化处理
	min_max_scaler = preprocessing.MinMaxScaler()
	X_minMax = min_max_scaler.fit_transform(data)
	print X_minMax[10:,:]
	kmean = KMeans(n_clusters=4, random_state=5)
	kmean.fit(X_minMax)
	# batch_size = 45
	# mbk = MiniBatchKMeans(n_clusters=10, batch_size=batch_size,n_init=10,         
                            max_no_improvement=10, verbose=0).score().fit(df_shop)
	print kmean.labels_
	print pd.Series(kmean.labels_).value_counts()
	print metrics.calinski_harabaz_score(X_minMax, kmean.labels_)
	label = pd.Series(kmean.labels_)
	data["label"] = label
	print "--------------------------------------"

最后我们用粗略的K值进行K-Means进行聚类（也可以令K=5、6，进行多次聚类，对比聚类效果），最终将得到的label保存下来。