机器学习笔记 十：基于神经网络算法的数据预测

本次的数据集为手写体数据

1.数据导入及y样本集的处理

one-hot：(5000, 10)

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat
from sklearn.preprocessing import OneHotEncoder

data = loadmat('E:\\MachineLearning\\PythonSet\\number.mat')

# sklearn中的OneHotEncoder,将y（向量）：5000*1转换为 y：5000*10的矩阵
# 所以这里不用向MATLAB一样，编写一个程序实现onehot功能
encoder = OneHotEncoder(sparse=False)
y_onehot = encoder.fit_transform(y)
y_onehot.shape

数据查看：

X = data['X']
y = data['y']
X.shape, y.shape

((5000, 400), (5000, 1))

2. 前向传播算法实现（正则化）

# sigmoid function
def sigmoid(z):
    return 1 / (1 + np.exp(-z))


# forward propagate function
def forward_propagate(X, theta1, theta2):
    # 计算样本数5000个(0：行数，1：列数)
    m = X.shape[0] 
    
    # axis=0：在行方向上插入，1：在列方向上插入
    a1 = np.insert(X, 0, values=np.ones(m), axis=1)
    z2 = a1 * theta1.T
    
    # 在a2矩阵前插入1
    a2 = np.insert(sigmoid(z2), 0, values=np.ones(m), axis=1)
    z3 = a2 * theta2.T
    
    h = sigmoid(z3)
    
    return a1, z2, a2, z3, h


# cost function（正则化）
def cost_reg(params, input_size, hidden_size, num_labels, X, y, learning_rate):
    m = X.shape[0]
    X = np.matrix(X)
    y = np.matrix(y)
    
    # 将参数数组重塑为参数矩阵
    theta1 = np.matrix(np.reshape(params[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1)))) # 重塑为 25*401
    theta2 = np.matrix(np.reshape(params[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1)))) # 重塑为 10*26
    
     # 运行前向传播算法
    a1, z2, a2, z3, h = forward_propagate(X, theta1, theta2)
    
    # 计算代价
    J = 0
    # 循环5000次
    for i in range(m):
        first_term = np.multiply(-y[i,:], np.log(h[i,:]))
        second_term = np.multiply((1 - y[i,:]), np.log(1 - h[i,:]))
        J += np.sum(first_term - second_term)
    
    J = J / m
     # 进行正则化处理(防止过拟合)
    J += (float(learning_rate) / (2 * m)) * (np.sum(np.power(theta1[:,1:], 2)) + np.sum(np.power(theta2[:,1:], 2))) # 计算theta1和theta2的平方之和
    
    return J

# 初始化设置
input_size = 400
hidden_size = 25
num_labels = 10
learning_rate = 10

# 随机初始化参数矩阵theta1、theta2
params = (np.random.random(size=hidden_size * (input_size + 1) + num_labels * (hidden_size + 1)) - 0.5) * 0.25
m = X.shape[0]
X = np.matrix(X)
y = np.matrix(y)

# 将参数数组解开为每个层的参数矩阵
theta1 = np.matrix(np.reshape(params[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
theta2 = np.matrix(np.reshape(params[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))

theta1.shape, theta2.shape

((25, 401), (10, 26))

a1, z2, a2, z3, h = forward_propagate(X, theta1, theta2)
a1.shape, z2.shape, a2.shape, z3.shape, h.shape

((5000, 401), (5000, 25), (5000, 26), (5000, 10), (5000, 10))

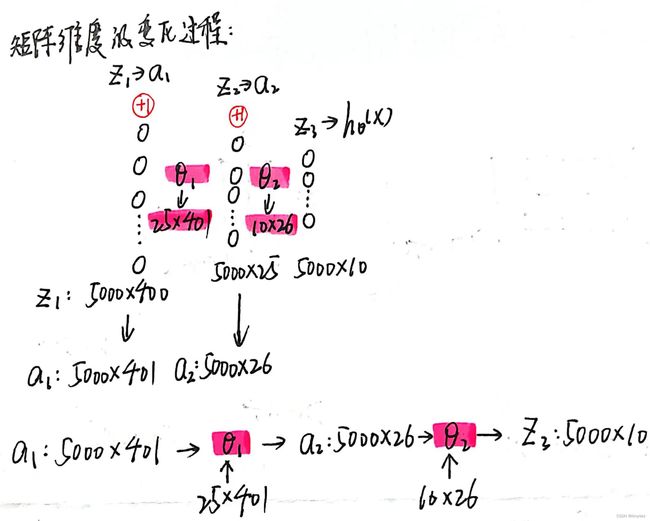
我认为上面所求的矩阵的维度是非常重要的，它能够帮助我们理清前向传播的思路，需要重点关注此处！！！

cost_reg(params, input_size, hidden_size, num_labels, X, y_onehot, learning_rate)

cost：6.95374626979026

3.后向传播算法

# sigmoid函数梯度（导数）：y * (1-y)
def sigmoid_gradient(z):
    return np.multiply(sigmoid(z), (1 - sigmoid(z)))


# 反向传播算法BP：
def backprop(params, input_size, hidden_size, num_labels, X, y, learning_rate):
    m = X.shape[0]
    X = np.matrix(X)
    y = np.matrix(y)
    
    # 将参数数组重塑为参数矩阵
    theta1 = np.matrix(np.reshape(params[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
    theta2 = np.matrix(np.reshape(params[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))
    
    # 运行前向传播算法
    a1, z2, a2, z3, h = forward_propagate(X, theta1, theta2)
    
    # initializations
    # 获得正确的参数delta的维度
    J = 0
    delta1 = np.zeros(theta1.shape)  # (25, 401)
    delta2 = np.zeros(theta2.shape)  # (10, 26)
    
    # 计算代价
    for i in range(m):
        first_term = np.multiply(-y[i,:], np.log(h[i,:]))
        second_term = np.multiply((1 - y[i,:]), np.log(1 - h[i,:]))
        J += np.sum(first_term - second_term)
    
    J = J / m
    
    # 正则化
    J += (float(learning_rate) / (2 * m)) * (np.sum(np.power(theta1[:,1:], 2)) + np.sum(np.power(theta2[:,1:], 2)))
    
    # 计算后向传播算法BP
    for t in range(m):
        a1t = a1[t,:]  # (1, 401)
        z2t = z2[t,:]  # (1, 25)
        a2t = a2[t,:]  # (1, 26)
        ht = h[t,:]  # (1, 10)，预测值
        yt = y[t,:]  # (1, 10)，实际值
        
        d3t = ht - yt  # (1, 10)
        
        z2t = np.insert(z2t, 0, values=np.ones(1))  # (1, 26)
        # np.multiply():元素乘法，非矩阵乘法
        d2t = np.multiply((theta2.T * d3t.T).T, sigmoid_gradient(z2t))  # (1, 26)
        
        delta1 = delta1 + (d2t[:,1:]).T * a1t
        delta2 = delta2 + d3t.T * a2t
        
    delta1 = delta1 / m
    delta2 = delta2 / m
    
    # 正则化
    delta1[:,1:] = delta1[:,1:] + (theta1[:,1:] * learning_rate) / m
    delta2[:,1:] = delta2[:,1:] + (theta2[:,1:] * learning_rate) / m
    
    # unravel the gradient matrices into a single array
    grad = np.concatenate((np.ravel(delta1), np.ravel(delta2)))
    
    return J, grad

J, grad = backprop(params, input_size, hidden_size, num_labels, X, y_onehot, learning_rate)
J, grad.shape

(6.95374626979026, (10285,))

4.最小化目标函数（cost function）

from scipy.optimize import minimize

# 最小化目标函数（cost function）
# 该过程比较耗时
fmin = minimize(fun=backprop, x0=params, args=(input_size, hidden_size, num_labels, X, y_onehot, learning_rate), 
                method='TNC', jac=True, options={'maxiter': 250})
fmin

这里的代价为0.99，虽然不是很低，但是对于这个例子来说也足够了，如果想让代价更低一些，可以调整学习率来实现。

5.预测新样本

# 使用前向传播算法对新样本进行预测
X = np.matrix(X)
theta1 = np.matrix(np.reshape(fmin.x[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
theta2 = np.matrix(np.reshape(fmin.x[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))

a1, z2, a2, z3, h = forward_propagate(X, theta1, theta2)
y_pred = np.array(np.argmax(h, axis=1) + 1)

correct = [1 if a == b else 0 for (a, b) in zip(y_pred, y)]
accuracy = (sum(map(int, correct)) / float(len(correct)))
print ('accuracy = {0}%'.format(accuracy * 100))

accuracy = 93.76%

NN思路：