Kaggle数据科学竞赛-数据分析流程笔记（以Give Me Some Credit为例）（未完待续~）

1. 赛题阅读

小节提要

  该阶段需要确定，问题的类型（分类or回归），模型的评估标准等。
  算法竞赛中对于赛题背景的业务挖掘点到即止即可，一方面是因为出于保密性要求，竞赛主办方会刻意隐藏部分信息，脱敏、创造新字段、甚至是不给出字段解释都是常见方法；另一方面，对于机器学习来说，重数字规律可能会强于重业务逻辑。
  如果碰到较为复杂的赛题，可以看论坛老哥们是怎么解读的。

1.1 赛题背景

  信用评分算法是银行用来确定是否应该发放贷款的方法，它对违约概率进行猜测。这项竞赛要求参赛者通过预测未来两年某人遭遇财务困境的可能性，提高信用评分的最新水平。

1.2 赛题目标

  本次竞赛的目标是建立一个借款人可以用来帮助做出最佳财务决策的模型，模型的评估标准为AUC。提供了250000名借款人的历史数据，奖金总额为5000美元。

2. 数据初见

小节提要

  这一个步骤主要是将数据导入编程环境当中，然后看一下数据大概是一个什么情况。然而这一步看似简单，实际上对于一些较为复杂的问题，可能会出现，数据量巨大内存无法直接读入，或者所给的表有很多张等等。
  遇到数据量较大的问题，一个办法是不要把数据下载到本地，利用kaggle notebook可以直接挂载比赛的数据；论坛老哥可能会将数据（原csv格式）转化为占用内存更小的其他格式，可以关注论坛，直接导入别人已经处理好的数据集。

2.1 各表数据

  数据字典

data_dictionary = pd.read_excel('../input/GiveMeSomeCredit/Data Dictionary.xls', header=1)

  数据字典当中记录了训练集表的各个字段含义，这些具有实际意义的特征对于后续建模过程中，特征工程很有帮助。

  示例提交

sample_submission = pd.read_csv('../input/GiveMeSomeCredit/sampleEntry.csv')

  这张表是为了告诉你，最终提交应该按照什么格式。

  训练集

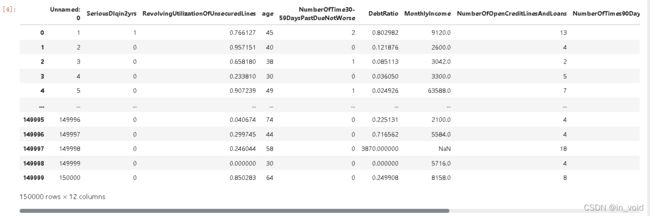
train = pd.read_csv('../input/GiveMeSomeCredit/cs-training.csv')

  与数据字典所展示的内容相同，该训练集共有10个特征，具体含义可以看数据字典。一共有150000行数据。该数据集算比较小的问题了，而且数据集特征的含义都给出来了，没有匿名特征。

  需要预测的变量为“SeriousDlqin2yrs”，取值为0-1，显然这回是一个二分类问题，同时也可以看作是一个0-1回归问题，使用逻辑回归类似的方法进行处理。

  测试集

test = pd.read_csv('../input/GiveMeSomeCredit/cs-test.csv')

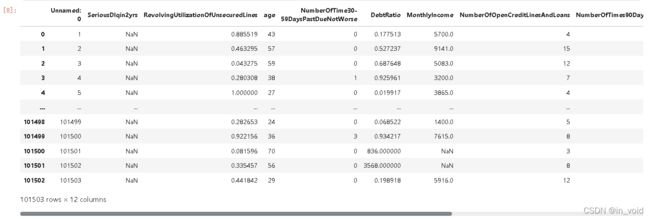
  测试比训练集稍小，除此之外，测试集的“SeriousDlqin2yrs”全为空值，需要我们去填。

3. 数据探索

小节提要

  本节将针对训练集与测试集进行较为细致的探索。

3.1 训练集探索

字段	解释	类型
SeriousDlqin2yrs	贷款逾期超过90天及以上的人（目标变量）	Y/N
RevolvingUtilizationOfUnsecuredLines	信用卡和个人信用额度（不包括房地产和汽车贷款等分期付款债务）的’总余额‘除以’信用额度之和‘	percentage
age	借款人年龄（年）	integer
NumberOfTime30-59DaysPastDueNotWorse	借款人逾期30-59天的次数，但在过去2年中没有恶化	integer
DebtRatio	负债比率：’每月债务偿还额、赡养费、生活费‘除以’每月总收入‘	percentage
MonthlyIncome	月收入	real
NumberOfOpenCreditLinesAndLoans	未结贷款的数量(分期付款，如汽车贷款或抵押贷款)和信用额度（如信用卡）	integer
NumberOfTimes90DaysLate	90天逾期次数：借款者有90天及以上逾期的次数	integer
NumberRealEstateLoansOrLines	不动产贷款或额度数量：抵押贷款和不动产放款包括房屋净值信贷额度	integer
NumberOfTime60-89DaysPastDueNotWorse	借款人逾期60-89天的次数，但在过去2年中没有恶化	integer
NumberOfDependents	家属数量：不包括本人的家属数量	integer

查看训练集的基本情况

train.info()

可以看到，“MonthlyIncome”与“NumberOfDependents”应该是存在缺失值的。

3.2 测试集探索

test.info()

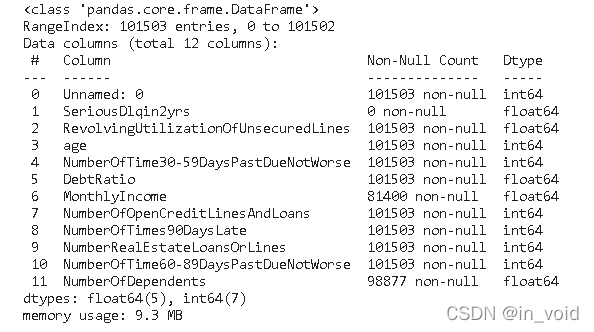
可以看到，测试集的“MonthlyIncome”与“NumberOfDependents”也是存在缺失值的。

4. 数据质量分析

小节提要

  本节将针对所给的全部数据进行分析。在实际建模过程中，首先我们会先校验数据的正确性，并检验缺失值、异常值等情况。

4.1 数据正确性校验

  所谓数据正确性，指的是数据本身是否符合基本逻辑，例如此处id作为建模分析对象独一无二的标识，我们需要验证其是否确实独一无二，并且训练集和测试集id无重复。

# 检验训练集id无重复
train['Unnamed: 0'].nunique() == train.shape[0]

# 检验测试集id无重复
test['Unnamed: 0'].nunique() == test.shape[0]

# 检验训练集和测试集id都是唯一值
test['Unnamed: 0'].nunique()+train['Unnamed: 0'].nunique()  == len(set(test['Unnamed: 0'].values.tolist() + train['Unnamed: 0'].values.tolist()))

结果为：训练集、测试集各自的id都是唯一值，都是从1到n（n为数据集长度）的自然数编码。

4.2 检验数据缺失情况

# 按列求缺失值并汇总
train.isnull().sum()

# 按列求缺失值并汇总
test.isnull().sum()

结果为：训练集、测试集的特征中，“MonthlyIncome”与“NumberOfDependents”存在一定数量的缺失值，且“MonthlyIncome”的缺失数量不小，需要考虑使用一定的方法进行填补。

4.3 异常值

  接下来进行异常值检验。由于我们尚未对数据集特征进行预处理，因此我们先查看标签列的异常值情况。

train['SeriousDlqin2yrs'].value_counts()
train['SeriousDlqin2yrs'].plot(kind='hist')

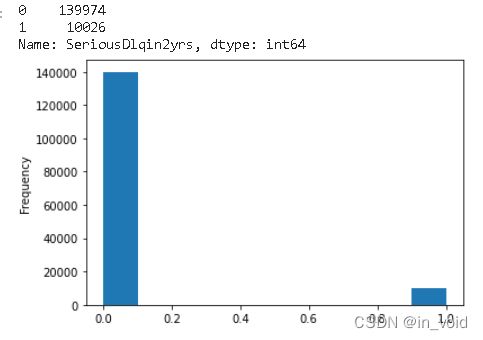
由于标签为0-1取值，并不是连续变量取值，因此没有必要判断是否符合正太分布，粗略地看了一下取值为0与取值为1地数量，可以看到两者之间是14：1的比例关系。

显然这里是没有出现异常值的。

4.4 规律一致性分析

  接下来，进行训练集和测试集的规律一致性分析。
  所谓规律一致性，指的是需要对训练集和测试集特征数据的分布进行简单比对，以“确定”两组数据是否诞生于同一个总体，即两组数据是否都遵循着背后总体的规律，即两组数据是否存在着规律一致性。
  我们知道，尽管机器学习并不强调样本-总体的概念，但在训练集上挖掘到的规律要在测试集上起到预测效果，就必须要求这两部分数据受到相同规律的影响。一般来说，对于标签未知的测试集，我们可以通过特征的分布规律来判断两组数据是否取自同一总体。

4.4.1 单变量分析

  首先我们先进行简单的单变量分布规律的对比。
对于离散型变量的分布规律，我们可以通过相对占比分布（用某一离散取值的数量除以总数得到该离散取值的占比，某种意义上来说也就是概率分布）来进行比较。

  例如首先我们查看“NumberOfOpenCreditLinesAndLoans”的相对占比分布可以通过如下代码实现：

# 不同取值水平汇总后排序再除以样本总数
(train['NumberOfOpenCreditLinesAndLoans'].value_counts().sort_index()/len(train)).plot(kind='line')
(test['NumberOfOpenCreditLinesAndLoans'].value_counts().sort_index()/len(test)).plot(kind='line')

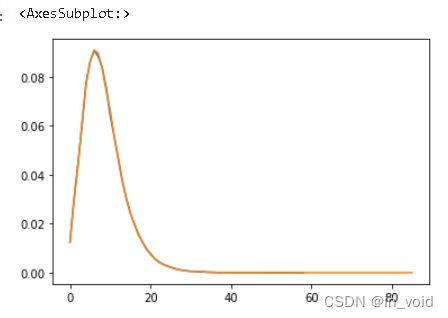
  其实这里是橙色线与蓝色线基本重合的，说明训练集与测试集的“NumberOfOpenCreditLinesAndLoans”特征分布相似，只是测试集会出现少数取值在60以上的数据。

  其余离散型变量也是一样的方法进行比较，此处不过多展示；连续型变量则可以直接画kde或hist图。

# 一些代码
# (train['age'].value_counts().sort_index()/len(train)).plot(kind='line')
# (test['age'].value_counts().sort_index()/len(test)).plot(kind='line')
# (train['NumberOfTime30-59DaysPastDueNotWorse'].value_counts().sort_index()/len(train)).plot(kind='line')
# (test['NumberOfTime30-59DaysPastDueNotWorse'].value_counts().sort_index()/len(test)).plot(kind='line')
# (train['NumberOfOpenCreditLinesAndLoans'].value_counts().sort_index()/len(train)).plot(kind='line')
# (test['NumberOfOpenCreditLinesAndLoans'].value_counts().sort_index()/len(test)).plot(kind='line')
# (train['RevolvingUtilizationOfUnsecuredLines']).plot(kind='hist')
# (test['RevolvingUtilizationOfUnsecuredLines']).plot(kind='hist')
# (train['RevolvingUtilizationOfUnsecuredLines']).plot(kind='kde')
# (test['RevolvingUtilizationOfUnsecuredLines']).plot(kind='kde')
# (train[train['RevolvingUtilizationOfUnsecuredLines']<1]['RevolvingUtilizationOfUnsecuredLines']).plot(kind='kde')
# (test[test['RevolvingUtilizationOfUnsecuredLines']<1]['RevolvingUtilizationOfUnsecuredLines']).plot(kind='kde')
# (train['NumberOfTime30-59DaysPastDueNotWorse']).plot(kind='kde')
# (test['NumberOfTime30-59DaysPastDueNotWorse']).plot(kind='kde')
# (train['MonthlyIncome']).plot(kind='kde')
# (test['MonthlyIncome']).plot(kind='kde')
# (train['NumberOfOpenCreditLinesAndLoans']).plot(kind='kde')
# (test['NumberOfOpenCreditLinesAndLoans']).plot(kind='kde')
# (train['NumberOfTimes90DaysLate']).plot(kind='kde')
# (test['NumberOfTimes90DaysLate']).plot(kind='kde')
# (train['NumberRealEstateLoansOrLines']).plot(kind='hist')
# (test['NumberRealEstateLoansOrLines']).plot(kind='hist')
# (train['NumberRealEstateLoansOrLines'].value_counts().sort_index()/len(train)).plot(kind='line')
# (test['NumberRealEstateLoansOrLines'].value_counts().sort_index()/len(test)).plot(kind='line')
# (train['NumberOfTime60-89DaysPastDueNotWorse']).plot(kind='hist')
# (test['NumberOfTime60-89DaysPastDueNotWorse']).plot(kind='hist')
# (train['NumberOfDependents']).plot(kind='kde')
# (test['NumberOfDependents']).plot(kind='kde')
# (train['NumberOfDependents'].value_counts().sort_index()/len(train)).plot(kind='line')
# (test['NumberOfDependents'].value_counts().sort_index()/len(test)).plot(kind='line')

  其中“DebtRatio”存在部分数据>1，这可能是因为该用户的月收入数据为空，于是数据制作者将负债直接除以了1。这里可以想到，能够还原出特征“Debt”负债值。

4.4.2 多变量联合分布

  接下来，我们进一步查看联合变量分布。所谓联合概率分布，指的是将离散变量两两组合，然后查看这个新变量的相对占比分布。例如特征1有0/1两个取值水平，特征2有A/B两个取值水平，则联合分布中就将存在0A、0B、1A、1B四种不同取值水平，然后进一步查看这四种不同取值水平出现的分布情况。

  首先我们可以创建如下函数以实现两个变量“联合”的目的：

def combine_feature(df):
    cols = df.columns
    feature1 = df[cols[0]].astype(str).values.tolist()
    feature2 = df[cols[1]].astype(str).values.tolist()
    return pd.Series([feature1[i]+'&'+feature2[i] for i in range(df.shape[0])])

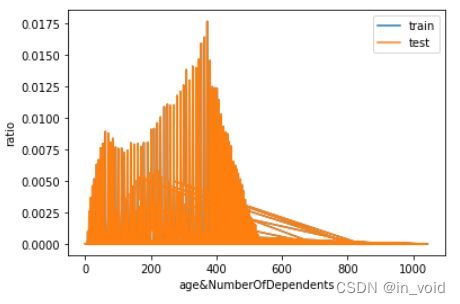
  这里将“age”与“NumberOfDependents”这两个变量进行“联合”，并绘制图像。

# 选取两个特征
cols = ['age', 'NumberOfDependents']

# 查看合并后结果
train_com = combine_feature(train[cols])

# 进一步计算占比分布
train_dis = train_com.value_counts().sort_index()/len(train)
test_dis = combine_feature(test[cols]).value_counts().sort_index()/len(test)

# 创建新的index
index_dis = pd.Series(train_dis.index.tolist() + test_dis.index.tolist()).drop_duplicates().sort_values()

# 对缺失值填补为0
(index_dis.map(train_dis).fillna(0)).plot()
(index_dis.map(train_dis).fillna(0)).plot()

# 绘图
import matplotlib.pyplot as plt
plt.legend(['train','test'])
plt.xlabel('&'.join(cols))
plt.ylabel('ratio')
plt.show()

  其余变量联合过程省略。。。

  能够发现所有联合变量的占比分布基本一致。数据集整体质量较高，且基本可以确认，训练集和测试集取自同一样本总体。

4.4.3 规律一致性分析的实际作用

  在实际建模过程中，规律一致性分析是非常重要但又经常容易被忽视的一个环节。通过规律一致性分析，我们可以得出非常多的可用于后续指导后续建模的关键性意见。通常我们可以根据规律一致性分析得出以下基本结论：

  (1).如果分布非常一致，则说明所有特征均取自同一整体，训练集和测试集规律拥有较高一致性，模型效果上限较高，建模过程中应该更加依靠特征工程方法和模型建模技巧提高最终预测效果；

  (2).如果分布不太一致，则说明训练集和测试集规律不太一致，此时模型预测效果上限会受此影响而被限制，并且模型大概率容易过拟合，在实际建模过程中可以多考虑使用交叉验证等方式防止过拟合，并且需要注重除了通用特征工程和建模方法外的trick的使用；

  至此，我们就完成了核心数据集的数据探索，接下来，我们还将围绕其他的补充数据进行进一步的数据解读与数据清洗，并为最终的建模工作做好相关准备。

5. 数据预处理

小节提要

  一般来说，在数据解读、数据探索和初步数据清洗都是同步进行的，都是前期非常重要的工作事项。其中，数据解读的目的是为了快速获取数据集的基本信息，通过比对官方给出的字段解释，快速了解数据集的字段含义，这对于许多复杂数据场景下的建模是非常有必要的。而数据探索，顾名思义，就是快速了解数据集的基本数据情况，主要工作包括数据正确性校验和数据质量分析，核心目的是为了能够快速了解各字段的基本情况，包括默认各字段的数据类型、数据集是否存在数据不一致的情况、数据集重复值情况、缺失值情况等，当然，通过一系列的数据探索，也能够快速加深对数据集的理解。当然，数据探索结束之后，就需要进行数据清洗了，所谓数据清洗，指的是在建模/特征工程之前进行的必要的调整，以确保后续操作可执行，包括数据字段类型调整、重复值处理、缺失值处理等等，当然，有些操作可能在后续会进行些许优化，比如数据清洗阶段我们可以先尝试进行较为简单的缺失值填补，在后续的建模过程中我们还可以根据实际建模结果来调整缺失值填补策略。
  我们也可将数据探索与数据清洗的过程总结如下：

5.1 离散/连续字段标注

  由于商户数据集中特征同时存在分类变量和离散变量，因此我们首先可以根据字段的说明对不同属性特征进行统一的划分：

  这里根据变量与实际含义的可能取值将变量分为离散型与连续型。

train.nunique()

category_cols = [
    'Unnamed: 0', 'SeriousDlqin2yrs', 'age', 'NumberOfDependents', 
    'NumberOfTime30-59DaysPastDueNotWorse', 'NumberOfOpenCreditLinesAndLoans', 
    'NumberOfTimes90DaysLate', 'NumberRealEstateLoansOrLines', 'NumberOfTime60-89DaysPastDueNotWorse']
numeric_cols = ['RevolvingUtilizationOfUnsecuredLines', 'DebtRatio', 'MonthlyIncome']

# 检验特征是否划分完全
assert len(category_cols) + len(numeric_cols) == train.shape[1]

5.2 离散变量数据处理

# 查看离散变量的缺失值情况
train[category_cols].isnull().sum()

  可以发现，“NumberOfDependents”缺失了近4000个数据，占训练集约3%，直接删去可能并不合适，因此需要考虑对其进行填充，这里先使用均值进行填充。

train['NumberOfDependents'] = train['NumberOfDependents'].fillna(round(train['NumberOfDependents'].mean()))

5.3 连续变量数据处理

# 查看连续变量的缺失值情况
train[numeric_cols].isnull().sum()

  可以发现，“MonthlyIncome”缺失了近30000个数据，占训练集约20%，直接删去可能并不合适，因此需要考虑对其进行填充，这里先使用均值进行填充。

train['MonthlyIncome'] = train['MonthlyIncome'].fillna(train['MonthlyIncome'].mean())

  此外，对于“RevolvingUtilizationOfUnsecuredLines”与“DebtRatio”两个特征需要处理。按照数据字典的解释，这两个特征应当是以比例的形式出现的，然而其中却出现了取值超过1的情况。

train[numeric_cols].describe()

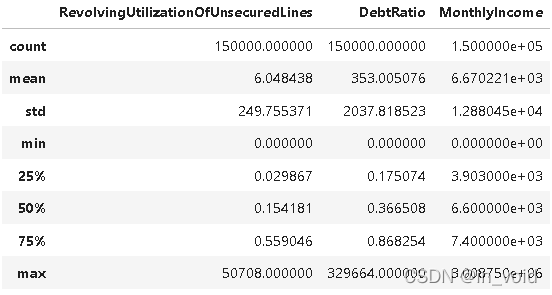
  对于“RevolvingUtilizationOfUnsecuredLines”特征，这里使用的是天花板盖帽法，直接将超过1的数全部赋值为1；而对于“DebtRatio”特征，由于其出现该情况是由于该数据对应的月收入数据的缺失，因此根据上文填充，这里将那些大于1的数据且月收入数据为空的，全部除以月收入的平均值，即对月收入列缺失值的填充值，再使用天花板盖帽法。

  注：由于这里需要判断月收入数据是否缺失，因此建议此处先做“RevolvingUtilizationOfUnsecuredLines”与“DebtRatio”特征的处理，再做缺失值的填充。

此处先不做过多的处理。

6. 特征工程

小节提要

  首先需要对得到的数据进一步进行特征工程处理。一般来说，对于已经清洗完的数据，特征工程部分核心需要考虑的问题就是特征创建（衍生）与特征筛选，也就是先尽可能创建/增加可能对模型结果有正面影响的特征，然后再对这些进行挑选，以保证模型运行稳定性及运行效率。当然，无论是特征衍生还是特征筛选，其实都有非常多的方法。此处为了保证公开课提供的思路和方法具有通用性，此处列举两种特征衍生的方法，即创建通用组合特征与业务统计特征；并在特征创建完毕后，介绍一种基础而通用的特征筛选的方法：基于皮尔逊相关系数的Filter方法进行特征筛选。这些方法都是非常通用且有效的方法，不仅能够帮助本次建模取得较好的成果，并且也能广泛适用到其他各场景中。

6.1 通用组合特征创建

// to do