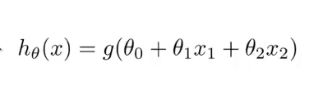机器学习算法笔记(1)——逻辑斯蒂回归Logistic处理二分类任务

本系列为观看吴恩达老师的 [中英字幕]吴恩达机器学习系列课程做的课堂笔记。图片来自视频截图。
不得不说，看了老师的视频真的学到了很多。即使数学不好的同志们也可以看懂，真的可谓是细致入微了。

一.逻辑斯蒂回归

1.模型

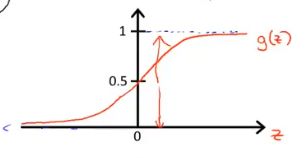
学过深度学习的同志们对这张图一定不陌生，它在神经网络中作为常用的激活函数，将输出值控制在0-1之间。他就是Sigmoid函数！当然它也被称为Logistic函数，这就是逻辑斯蒂回归算法的由来。

还有一点要注意的是，虽然名字叫做逻辑斯蒂回归，但他解决的其实是分类问题。其实原理很简单，对于二分类任务来说，大于0就是正类，小于0就是负类。对于多分类问题稍后再讨论。

def Sigmoid(x:np.array) -> np.array:
    return (1 / (1 + np.exp(-x)))

2.代价函数（损失函数）

即真实值为正类时，预测值越靠近1，损失越小，越靠近0，损失越大。

反之

简化之后

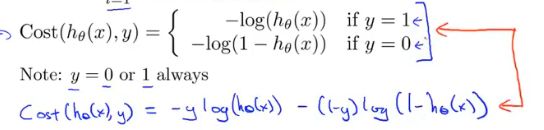
y为正类时，后一项为0，y为负类时，前一项为0。

最终的损失函数定义为：

是不是很眼熟？它就是大名鼎鼎的交叉熵损失函数的特殊形式！

pred为预测值，y为真实值，X为原始样本。
返回值前者为各个参数的损失值

3.优化算法

这里我们选择梯度下降算法。关于梯度下降具体介绍，这里不做延伸。只给出公式

alpha为学习率，后面的对损失函数的偏导可以写成这样的形式

看着复杂，其实就是同时更新所有的参数。注意要是同时喔。所以通过循环可以实现，但更推荐通过矩阵运算实现，这样更简洁高效。

配合代码更好理解~

def LossFuntion(pred, y, X):
    m = len(pred)
    sumloss = 0
    for i,j,z in zip(pred, y, X):
        sumloss+= (i-j) * z 
    return sumloss/m

def GrandDesent(w, loss, alpha=0.01):
    update = w.T - alpha*loss
    return update

二.代码实现

1.二维二分类

这次使用鸢尾花数据集。先导包

import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

读数据，这次我们只选择两个维度的数据

iris = load_iris()
X = iris["data"][:100, :]
y = iris["target"][:100].reshape(-1, 1)

plt.scatter(X[:, 0], X[:, 1], c=y)

参数初始化

w = np.ones(3).reshape(-1, 1)  #初始化权值
X = np.insert(X, 0, values=1, axis=1)  #偏执项
maxiter = 5000  #迭代次数

开始迭代

for i in range(maxiter):
    
    pred = Sigmoid(np.dot(X, w))      #得到预测值
    
    loss = LossFuntion(pred, y, X)    #计算loss
    
    w = GrandDesent(w, loss=loss).T   #权值更新

可以看到全部用矩阵运算大大减少了代码量，更具逼格也更好看，肥肠的方便。

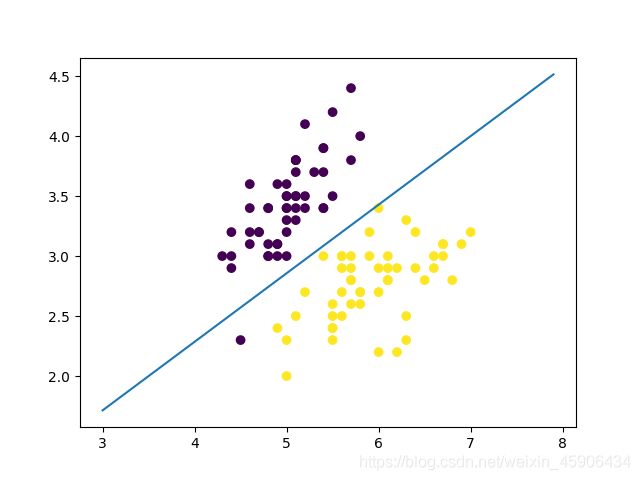
迭代结束后，我们随机初始化的权值已经找到了一条决策边界，将多数的数据成功分成两类了，我们可视化出来。

x = np.arange(3.0, 8, 0.1)
y = (-w[0] - w[1]*x) / w[2]
plt.plot(x, y)
plt.show()

这里的y的公式怎么来的呢

也就是

x = np.arange(3.0, 8, 0.1)
y = (-w[0] - w[1]*x) / w[2]
plt.plot(x, y)
plt.show()

虽然有一个错分类了，但是效果还不错

2.多维二分类

由于三维之上的数据无法可视化，所以选择三维数据

X = data["data"][:, :3][:100, :]
y = data["target"][:100].reshape(-1, 1)
w = np.ones(4).reshape(-1, 1)

ax = plt.axes(projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y)

x1 = np.arange(1, 8, 0.1)
x2 = np.arange(1, 8, 0.1)
X, Y = np.meshgrid(x1, x2)    

y = (-w[0] - w[1]*X - w[2]*Y) / w[3]
ax.plot_surface(X, Y, y, color='red')
plt.show()

增加一个维度后，错分类的数据成功正确分类，可见增加维度有时能取得更好的效果。

且听下回分解