备战蓝桥杯--双指针和三指针（尺取法）

尺取法定义：将i，j两重循环，转化为一个循环，但是要满足j于i有关系（j依赖于i），主要是为了降低算法的复杂度，减少循环的使用

双指针的应用

时间复杂度为O(n)
1.反向扫描：一左一右，同时向中间走，两者满足某些条件时进行操作
2.同向扫描：i、j方向相同，速度不同，i、j之间在序列上产生了一个大小可变的“滑动窗口”，窗口大小不断变化，伸缩前进
注意窗口的大小不是固定不变的，一定是不断伸缩的

反向扫描案例：快速排序 （指向同一个序列）
正向扫描案例：两个有序子列的归并 （指向两个不同序列）
竞赛什么时候用：满足两个指针是单调的才能用，单调是指当i不断向右移的时候，j要么单调向左移动，要么单调向右移动（只能是其中一个）

案例一、最长连续子序列：

题目链接：https://www.acwing.com/problem/content/description/4397/
分析：是否能用双指针来做（i和j是否单调）
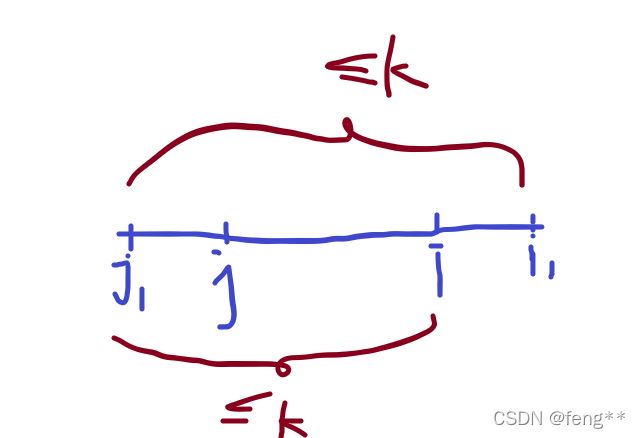
首先定义i和j，i–不超过k个不同数的序列的最右端的位置，j–不超过k个不同数的序列的最左端的位置
考虑假设当i往后移动到i1,j假设往前移动到j1，成不成立
这种情况下i对应的左端点应该为j1，与j矛盾，所以当i往后走的时候，j也一定是往后走的，满足条件

AC代码：
写代码的时候，考虑往窗口里放一个数，会怎样，什么时候从窗口中删掉一个数，每次i都会往后移动，但是窗口每次要么增加一个数，要么删掉一个数，尽量不同时操作
这个题数据量达到50万，特别容易超时，cin耗时是scanf的两倍，第一种一个一个地移动的过不了，第二种1888ms

#include
#include
using namespace std;
#define MAXSIZE 500005
int a[MAXSIZE];
int n,k; 
int cnt[1000002];
int main()
{
	scanf("%d %d",&n,&k);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
	}
	int i=1,j=1,t=0,r=1,l=1;
	while(i<=n)
	{   //往窗口中加入一个数 
		if(!cnt[a[i]])  //新加进来的数没有在窗口中
		{
			if(t<k)  //能加 
			{
				cnt[a[i]]++; 
				t++; //连续序列不同元素的长度增加 
			}
			else  //窗口里的不同数个数太多了，该缩小窗口大小了 
			{
				cnt[a[j]]--;
				if(cnt[a[j]]==0) t--;   
				j++;i--; //i没有添加成功，停在当前位置 
			}
			
		}
		else cnt[a[i]]++; 
		if(i-j+1>r-l+1)
		{
			r=i;l=j;  //更新最长序列的左右端点 
		}
		i++;
	}
	printf("%d %d",l,r);
	return 0;
} 

每次当区间不同数字的个数大于k时用循环移动左指针，直到满足要求，这个版本更快一些

#include
#include
using namespace std;
int n,k;
int num[10000000];
int in[500005];
int main()
{
	scanf("%d %d",&n,&k);
	for(int i=1;i<=n;i++) scanf("%d",&in[i]);
	int l=1,r=1,s=1,e=1;
	int deff=0;
	while(r<=n)
	{
		if(num[in[r]]==0) deff++;  //区间里面没有这个数 
		num[in[r]]++;   //加进区间内 
		r++;
		while(deff>k)  //区间的不同的数大于k了 
		{
			num[in[l]]--;
			if(num[in[l]]==0) deff--;
			l++;
		}
		if(r-l>e-s) 
		{
			s=l;e=r;
		}
	}
	printf("%d %d",s,--e);
	return 0;
}

三指针的应用

当数组有重复数字时用三指针，i是主指针，从头到尾遍历n个数，j、k是辅助指针，用于查找数字相同的区间[i,j]

案例一、日志统计

题目链接：http://oj.ecustacm.cn/problem.php?id=1373
AC代码及分析：

#include
using namespace std;
#define MAXSIZE 100002
int zan[MAXSIZE];
int is_re[MAXSIZE];
struct Node
{
	int time;
	int id;
};
Node data[MAXSIZE];
bool cmp(Node a,Node b)
{
	return a.time<b.time;
}
//首先题目给出了我们一个固定的区间，我们滑动窗口的区间一定是该区间的子集
//窗口以外的赞我们不考虑，进入窗口增加赞，离开窗口减少赞 
//即要滑动一个时间的区间，首先应将时间排序，按照时间顺序判断 
int main()
{
	int n,d,m;
	cin>>n>>d>>m;
	for(int i=0;i<n;i++)
	{
		cin>>data[i].time>>data[i].id;
	}
	sort(data,data+n,cmp);
	int j=0,k=0,i=0;  //i是主指针，当主指针遍历完整个数组后结束滑动窗口 
	while(i<n)      //[j,i)是当前窗口   [j,k)是时间相同的区间，注意都是前闭后开 
	{
		while(data[k].time==data[j].time)  //一步到位，确定时间相同的区间 
		{
			k++;
		}
		if(data[i].time-data[j].time<d)  //当前窗口过小 ，能继续增大 
		{
			zan[data[i].id]++;    //每将一个记录纳入进滑动窗口时都要判断该记录对应的id赞是否达到要求 
			if(zan[data[i].id]>=m)    
			is_re[data[i].id]=1;   //不能用容器将满足条件的id装起来，有可能重复 
			i++; 
		}
		else                             //当前窗口太大，缩小窗口 
		{
			while(j<k)             //跳过当前时间对应的所有记录，则j要走到k的位置，一边走一边将窗口以外的id的赞删除 
			{                      //注意是一步步走过去，不是直接跳过去，因为要将赞清除 
				zan[data[j].id]--;
				j++;
			}
		}
		
	}
	for(int i=0;i<MAXSIZE;i++)
	{
		if(is_re[i]) cout<<i<<endl;
	}
	return 0;
}

案例二、螺旋折线

题目链接：http://oj.ecustacm.cn/problem.php?id=1372

扩展：四指针

题目链接：http://118.190.20.162/view.page?gpid=T127

这个题运用模拟的思路，如果不采用指针的方法，使用暴力枚举会超时，运用指针就能大大减小耗时
在写代码过程中时刻模拟指针的移动，定义上下左右四个指针分别代表矩形的上下左右四条边
AC代码：

#include
using namespace std;
#define MAXSIZE 1000 
int n,L,r,t;
int G[MAXSIZE][MAXSIZE];
int main()
{
	cin>>n>>L>>r>>t;
	for(int i=0;i<n;i++)
	{
		for(int j=0;j<n;j++)
		{
			cin>>G[i][j];
		}
		
	}
	int ans=0;
	int s,x,z,y;    //定义4个指针，尽量使指针语义化，方便写和读
	int num=0,sum=0;
	s=0;x=r;	
	while(s<=n-r-1) 
	{
		sum=0;    //先求第一个
		num=0; 
		z=0;y=r;
		for(int i=s;i<=x;i++)
		{
			for(int j=z;j<=y;j++)
			{
				sum+=G[i][j];
				num++;
			}
			
		}
		if(sum*1.0/num<=t) ans++;
		while(z<n-r-1)   //再不断往右移求剩下的n-1个 
		{
			if(y<n-1)   //右指针能往右移就往右走 
			{
				y++;    //将矩形右边边上的点加入 
				for(int i=s;i<=x;i++) 
				{
					sum+=G[i][y];
					num++;
				}
			}
			
			if(y>2*r)   //右指针移动到某个条件时左指针开始移动 
			{            //将左指针即矩形左边边上的点从矩阵中删去 
				for(int i=s;i<=x;i++) 
				{
					sum-=G[i][z];
					num--;
				}
				z++;
			}
			if(sum*1.0/num<=t) ans++;
		//	cout<
		}
		
		if(x<n-1) x++;  //下指针满足条件时往下移 
		if(x>2*r) 	s++;  //当下指针移动到某个条件时上指针往下移 
		
	}
	cout<<ans; 
	return 0;
}