python实战因子分析和主成分分析
机器学习中,因子分析和主成分分析是模型降维的两种最常用方法。
因子分析基础概念
因子分析是一种统计方法,可用于描述观察到的相关变量之间的变异性,即潜在的未观察到的变量数量可能更少(称为因子)。例如,六个观察变量的变化可能主要反映了两个未观察(基础)变量的变化。因子分析搜索这种联合变化,以响应未观察到的潜在变量。将观察到的变量建模为潜在因素以及“错误”项的线性组合。
简而言之,变量的因子加载量化了变量与给定因子相关的程度。
因子分析方法背后的一个普遍原理是,有关观察到的变量之间的相互依赖性的信息可以稍后用于减少数据集中的变量集。因子分析通常用于生物学,心理计量学,人格理论,市场营销,产品管理,运营研究和财务。在有大量观察到的变量被认为反映较少数量的基础/潜在变量的数据集时,这可能会有所帮助。它是最常用的相互依存技术之一,当相关变量集显示出系统的相互依存关系时使用,其目的是找出产生共同性的潜在因素。
主成分分析基础概念
主成分分析principal component analysis
通过考察变量相关性,找到几个主成分(principal component)来代表原来的多个变量。同时使她们尽量保留原始变量的信息。
这些变量 彼此不相关,数量远少于原始变量个数,从而达到数据降维目的。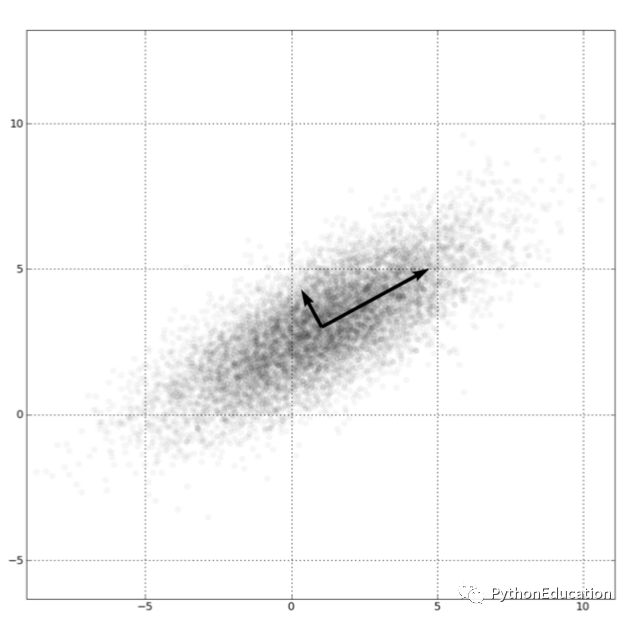
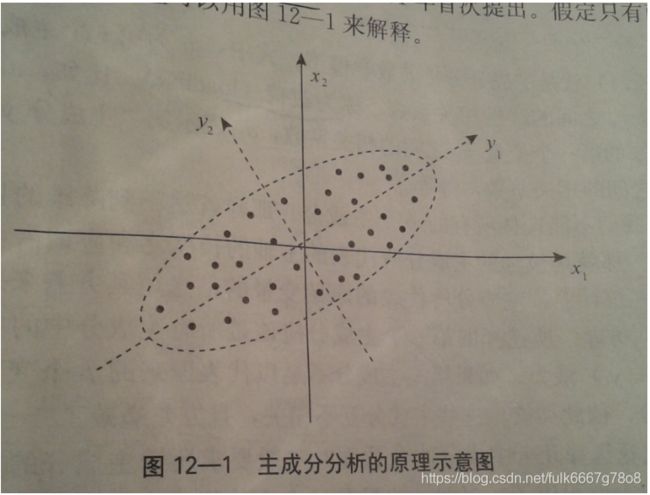
图中可见两个变量x1和x2存在相关关系,它们信息有重叠。如果把两个变量用一个新的变量表示,同时这一新变量可能包含原来的两个变量的信息,这就是降维过程。
散点图形成一个椭圆形轮廓,包含一个长轴和一个短轴,称为主轴。
在椭圆长轴方向,数据变化大,携带大部分数据变化信息。
在椭圆短轴方向,数据变化小。携带小部分数据变化信息。
因此用长轴y1方向就可以代表原来x1和x2两个变量信息,这样两个变量降维到一个变量,达到降维目的。
椭圆中,长短轴相差越大,长轴变量代表性就越好 ,降维越合理。
欢迎各位同学学习《python实战因子分析和主成分分析》
课程目录
章节1python编程环境搭建
课时1Anaconda下载安装
课时2Anaconda快速入门指南
课时3Anaconda Navigator导航器
课时4python第三方包安装(pip和conda install)
课时5Python非官方扩展包下载地址
章节2python项目实战主成分分析PCA
课时6边际效应基本概念
课时7模型维度与边际效应,变量越多越好吗?
课时8kaggle模型一定最好吗?降维在企业建模实际意义
课时9降维方法好不好,测试为准
课时10python主成分分析关键代码解读
课时11python主成分分析与机器学习建模结合项目实战
课时12PCA主成分降维在人脸识别应用-附代码
章节3python项目实战因子分析factor analysis
课时13因子分析基本思想和使用限制条件
课时14python sklearn因子分析实战乳腺癌数据集
课时15python因子分析第三方包训练模型,结果让人吃惊
课时16因子分析-KMO和巴特利球形度检验
课时17因子分析-python绘制碎石图
课时18因子分析旋转方法rotation
课时19因子分析-累计方差贡献率
课时20SPSS因子分析项目实操
章节4附录
课时21课程脚本和数据资料下载地址
课程脚本
课程部分文字介绍
因子分析基础概念
因子分析是一种统计方法,可用于描述观察到的相关变量之间的变异性,即潜在的未观察到的变量数量可能更少(称为因子)。例如,六个观察变量的变化可能主要反映了两个未观察(基础)变量的变化。因子分析搜索这种联合变化,以响应未观察到的潜在变量。将观察到的变量建模为潜在因素以及“错误”项的线性组合。
简而言之,变量的因子加载量化了变量与给定因子相关的程度。
因子分析方法背后的一个普遍原理是,有关观察到的变量之间的相互依赖性的信息可以稍后用于减少数据集中的变量集。因子分析通常用于生物学,心理计量学,人格理论,市场营销,产品管理,运营研究和财务。在有大量观察到的变量被认为反映较少数量的基础/潜在变量的数据集时,这可能会有所帮助。它是最常用的相互依存技术之一,当相关变量集显示出系统的相互依存关系时使用,其目的是找出产生共同性的潜在因素。
因子分析分为两类
因子分析重要部分是二变量相关性矩阵和因子的相关性
pattern matrix中灰色部分就是变量值高的,灰色变量具有代表性
因子分析算法步骤
因子分析是一种相关性分析方法,用于在大量变量中寻找和描述潜在因子
因子分析确认变量的相关性,把相关性强的变量归类为一个潜在因子
最早因子分析应用于二战后IQ测试。科学家试图把测试的所有变量综合为一个因子,IQ得分
下面表格数据,变量有1-6,其中变量1,3,4有相关性,它们可以融合为一个因子
一般来说,大量变量可以降维到少数几个因子。
紫色的变量1,3,4有相关性,可以归为一个因子
橙色变量2,6有相关性可以归为一个因子
综合上述,变量1,3,4归为一个因子
变量2,6,归为一个因子
变量5归为一个因子
这个数据集的6个变量降低维度到3个因子。
因子分析步骤:
1.因子分析假设条件
2.找到因子的方法
3.决定因子是否重要
4.检验因子里变量的交互性
因子分析假设
假设很重要,如果不符合假设条件,则报告可行性很差
因子分析有6个假设条件
1.没有异常值
2.足够样本量
3.没有完美多重相关性
4.不需要符合方差齐性
5.变量符合线性
6.数据符合间隔性
数据没有异常值,下例中1247943太大,属于异常值,应该排除
变量数量要多于因子数量
数据不能完全多重相关性
下表数据变量1*2得到变量2,变量1*3得到变量3
homoscedasticity方差齐性
变量不需要满足方差齐性
变量符合线性,方差分析基于线性前提
方差分析的变量至少是定距变量
分类变量,例如男女,定序变量1,2,3是均匀等差,也不行
(1) Norminal Data 定类变量:变量的不同取值仅仅代表了不同类的事物,这样的变量叫定类变量。问卷的人口特征中最常使用的问题,而调查被访对象的“性别”,就是 定类变量。对于定类变量,加减乘除等运算是没有实际意义的。
(2) Ordinal Data定序变量:变量的值不仅能够代表事物的分类,还能代表事物按某种特性的排序,这样的变量叫定序变量。问卷的人口特征中最常使用的问题“教育程度“,以及态度量表题目等都是定序变量,定序变量的值之间可以比较大小,或者有强弱顺序,但两个值的差一般没有什么实际意义。
(3)Interval Data 定距变量:变量的值之间可以比较大小,两个值的差有实际意义,这样的变量叫定距变量。有时问卷在调查被访者的“年龄”和“每月平均收入”,都是定距变量。
(4) Ratio Data 定比变量, 有绝对0点,如质量,高度。定比变量与定距变量在市场调查中一般不加以区分,它们的差别在于,定距变量取值为“0”时,不表示“没有”,仅仅是取值为0。定比变量取值为“0”时,则表示“没有”。
因子分析报告可信度
残差小于5%,KMO大于0.8,解释方差大于60%较好。
教育案例因子分析实例
what are the percentages of disciplinary placements,Afican-American,Hispanic,white,economically disadvantaged,limited English proficiency,at risk ,and special education students in Texas independent schooll districts in 2011?
2011年德克萨斯州独立学区的学科配置,非裔美国人,西班牙裔,白人,经济地位不利,英语能力有限,处于风险中,以及特殊教育学生的百分比是多少?
因子分析问题
下面八个变量是否存在相关性?学科配置,非裔美国人,西班牙裔,白人,经济地位不利,英语能力有限,处于风险中,以及特殊教育学生比例
因子分析工具选择:
1.spss
2.python
检验五项
1.描述性统计
2.共线矩阵
3.bartlett kmo检验
4.方差总量解释
5. 特征根图
6.旋转成分矩阵
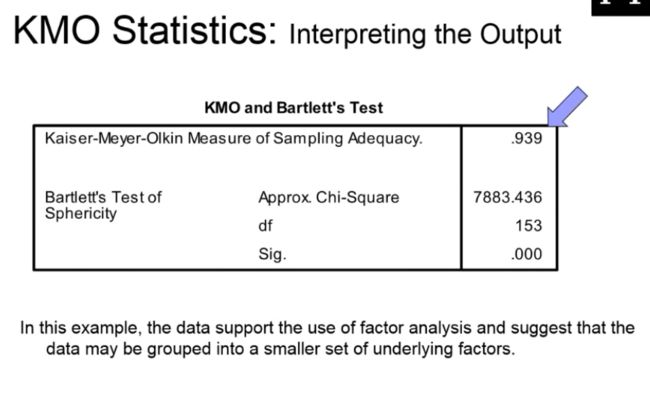
KMO检验
一般KMO值大于0.8参考意义较大
下图KMO值=0.54,说明相关性一般,可以勉强进行因子分析。
bartlett显著性0,拒绝零假设(变量无相关性),得到变量有显著相关性,有时候,bartlett意义不大
![]()
KMO(Kaiser-Meyer-Olkin)检验统计量是用于比较变量间简单相关系数和偏相关系数的指标。主要应用于多元统计的因子分析。KMO统计量是取值在0和1之间。
当所有变量间的简单相关系数平方和远远大于偏相关系数平方和时,KMO值接近1.KMO值越接近于1,意味着变量间的相关性越强,原有变量越适合作因子分析;当所有变量间的简单相关系数平方和接近0时,KMO值接近0.KMO值越接近于0,意味着变量间的相关性越弱,原有变量越不适合作因子分析。
Bartlett's球状检验是一种数学术语。用于检验相关阵中各变量间的相关性,是否为单位阵,即检验各个变量是否各自独立。因子分析前,首先进行KMO检验和巴特利球体检验。在因子分析中,若拒绝原假设,则说明可以做因子分析,若不拒绝原假设,则说明这些变量可能独立提供一些信息,不适合做因子分析。
如果变量间彼此独立,则无法从中提取公因子,也就无法应用因子分析法。Bartlett球形检验判断如果相关阵是单位阵,则各变量独立因子分析法无效。由SPSS检验结果显示Sig.<0.05(即p值<0.05)时,说明各变量间具有相关性,因子分析有效。
有些情况下,bartlett检验意义不大
共线矩阵
西班牙后裔比例与黑人比例中度冲突
西班牙后裔比例与白人比例严重冲突
西班牙后裔比例英语水平-0.54相关性,即西班牙后裔英语不好
非洲美国后裔比例与白人30%正相关冲突
英语水平差和经济收入低0.577正相关,与风险因子0.44正相关
scree plot
纵坐标:特征根值
横坐标:因子数量
方差解释
elgenvalue特征根选择大于1的因子,前三个因子特征根大于1,累计解释力度得到73.887%
我们的分析产生了3个旋转后的因子
旋转的成分矩阵分析
component1:西班牙裔比例,白人比例,黑人比例与经济落后,英语水平低,风险因素比较突出,这些因子可以归类为ethnicity种族问题
第二个因子:特殊需求(special education占比最大0.812)
第三个因子:黑人因子,占比0.96
因子旋转(factor rotation)下图:主成分1的列数来看,所有值都>0.5, 即主成分1能共同解释所有变量,而对每个变量x_i只能解释其中少部分信息,因子含糊不清,需要旋转。 而且主成分1解释了:财政收入,固定资产投资,社会消费品零售总额, 这三个变量难以综合解释。
旋转后,因子1能解释2,3,4,6变量,含义比旋转前要清晰。
因子1:财政收入,固定资产投资,年末总人口,社会消费品零售总额 -------命名为:经济水平
因子2:人均GDP,居民消费水平--------命名为:消费水平

因子旋转的目的使因子含义更加清楚,以便对因子命名和解释。
旋转方法:正交旋转和斜交旋转。
正交旋转是指坐标轴总是保持垂直90度旋转,这样新生成因子可保持不变。
斜交旋转坐标轴夹角是任意的,生成因子不能保证不相关。
实际中更多应用正交旋转Varimax法。
旋转方法:
Varimax
quartimax
equamax
direct oblimin(斜交旋转)
数学模型 设原始的p个变量为x1,x2......x_p, 要寻找k个因子(k
载荷 a_ij
含义与主成分类似。 a_ij为第i个变量x_i与第j个因子f_j之间的线性相关系数,反映x_i和f_j之间的相关程度,也称载荷。
f_i:公因子common factor
因子f_i出现在每个原始变量与因子的线性组合中,称为公因子。
特殊因子:代表公因子以外因素影响。
共同度量:h_i**2
考察x_i的信息能够被k个公因子所解释的程度。它是用k个公因子对第i个变量的方差贡献率来表示的,称为变量x_i的共同度量(communality)
计算公式如下图:
共同度量值越大,说明提出的公因子对原始变量的解释能力越强。
方差贡献率:
:第j个公因子的方差贡献率g_j**2
方差贡献率表示第j个 公因子对变量x_i所提供的方差总和,反应了第j个公因子的相对重要程度。方差贡献率越大表明该公因子对x_i的贡献越大。
变量共同度量表,由该表可知,所有变量的共同度量都是在90%以上,因此提取的公因子对原始变量解释力很强。
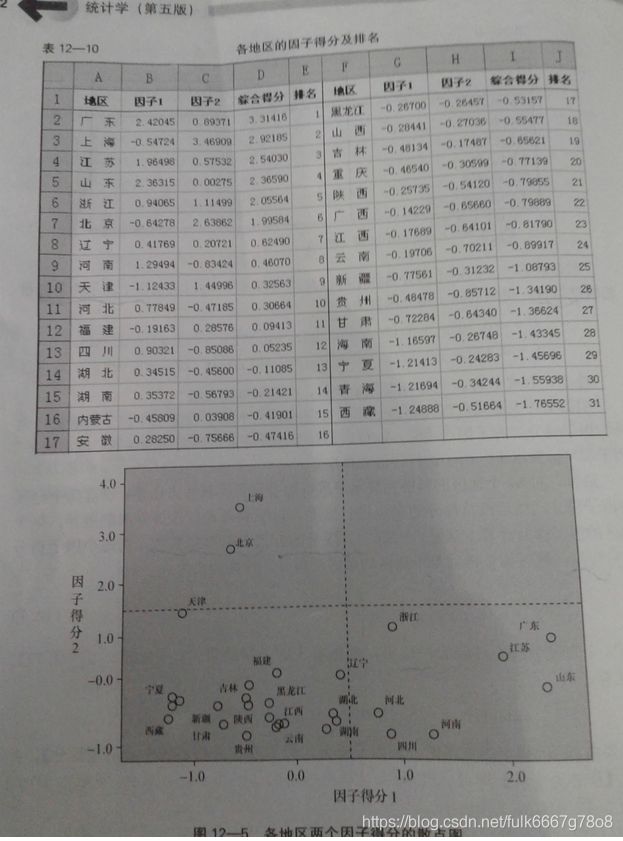
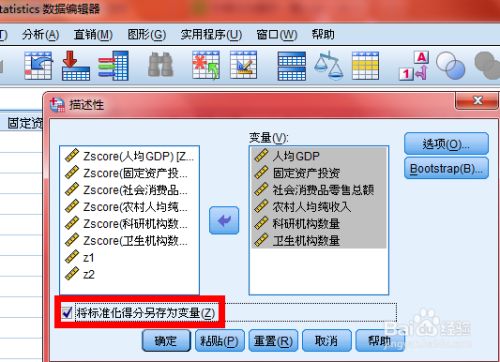
因子得分
spss操作:分析步骤---得分---保存为变量
程序自动统计得到结果
因子得分(factor score)
就是每个因子在每个样本上的具体取值。每个因子的得分实际上由下列因子得分函数给出
因子得分是各变量的线性组合。

f1=[-0.105,0.18,0.3,0.372,-0.104,0.281]
f2=[0.43,0.171,-0.026,-0.237,0.429,0.022]
beijing=[50467,11171514,3296.4,1581,16770,3275.2]
coefficient=[0.691141,0.308859]
f1_score=[]
f2_score=[]
for i in range(len(f1)):
score1=f1[i]*beijing[i]
score2=f2[i]*beijing[i]
f1_score.append(score1)
f2_score.append(score2)
f1_sum=sum(f1_score)
f2_sum=sum(f2_score)
factor_score=coefficient[0]*f1_sum+coefficient[1]*f2_sum
>>> factor_score
1985481.5535567512
运算结果和答案不符合,说明 x_i不是原始变量,而是标准化变量
特征根 eigenvalues['aɪgən,væljuː]
表中初始特征值就是特征根,实际上就是本例中的6个主轴长度。
特征根 eigenvalues
---即主轴或方差,当特征根小于1时,就不再选作主成分了。选择特征根大于1的值
主成分的累计方差贡献率达到80%以上的前几个主成分,都可以选作最后的主成分。
碎石图scree plot
scree[skriː] 小石子;岩屑堆
A scree plot displays the eigenvalues associated with a component or factor in descending order versus the number of the component or factor. You can use scree plots in principal components analysis and factor analysis to visually assess which components or factors explain most of the variability in the data. 碎石图用于主成分分析或因子分析
横轴是因子,纵轴是特征值
观察第五个因素后,斜率慢慢变缓,前五个因素解释了大部分原因。

A factor analysis was conducted on 12 different characteristics of job applicants. This scree plot shows that 5 of those factors explain most of the variability because the line starts to straighten after factor 5. The remaining factors explain a very small proportion of the variability and are likely unimportant.
The ideal pattern in a scree plot is a steep curve, followed by a bend and then a flat or horizontal line. Retain those components or factors in the steep curve before the first point that starts the flat line trend. You might have difficulty interpreting a scree plot. Use your knowledge of the data and the results from the other approaches of selecting components or factors to help decide the number of important components or factors.
碎石图中,前三个因子特征根值大于1,可以被筛选
载荷图Loading Plot
The loading plot is a plot of the relationship between the original variables and the subspace dimension. It is used to interpret relationships between variables.载荷图解释原始变量和主成分关系
横坐标表示第一主成分与原始变量之间的相关系数;纵轴表示第二主成分与原始变量之间相关系数。
这样每个变量对应的主成分载荷就对应坐标系中一个点,比如,人均GDP变量对应点是(0.67,0.725)。这样6个变量就有6个点。相关系数的点越远离坐标轴原点,主成分对原始变量的代表性就越大。
图中,人均GDP和居民消费水平几乎重合
主成分分析-降维
主成分分析principal component analysis
通过考察变量相关性,找到几个主成分(principal component)来代表原来的多个变量。
同时使她们尽量保留原始变量的信息。
这些变量 彼此不相关,数量远少于原始变量个数,从而达到数据降维目的。
图中可见两个变量x1和x2存在相关关系,它们信息有重叠。如果把两个变量用一个新的变量表示,同时这一新变量可能包含原来的两个变量的信息,这就是降维过程。
散点图形成一个椭圆形轮廓,包含一个长轴和一个短轴,称为主轴。
在椭圆长轴方向,数据变化大,携带大部分数据变化信息。
在椭圆短轴方向,数据变化小。携带小部分数据变化信息。
因此用长轴y1方向就可以代表原来x1和x2两个变量信息,这样两个变量降维到一个变量,达到降维目的。
椭圆中,长短轴相差越大,长轴变量代表性就越好 ,降维越合理。
多维变量情形类似,只不过是一个高维椭圆,无法直接观察。由于每个变量有一个坐标轴,因此有几个变量就有几个主轴。
首先找出椭圆球各个主轴,再用代表大多数数据信息的最长几个轴作为新变量,这样降维就完成了。
找出的新变量是原来变量的线性组合,叫做主成分。
三个提取因子方法
实战
实战1-寻找美国总统因子
变量包括:年龄,性别,种族等等
性别,种族属于分类变量,不适合因子分析
学生教学能力分为两个因子:
量化能力:数学得分,编程得分,物理得分
口语能力:英语,言语推理得分
PCA实例
下面我们用一个实例来学习下scikit-learn中的PCA类使用。为了方便的可视化让大家有一个直观的认识,我们这里使用了三维的数据来降维。
首先我们生成随机数据并可视化,代码如下:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
from sklearn.datasets.samples_generator import make_blobs
# X为样本特征,Y为样本簇类别, 共1000个样本,每个样本3个特征,共4个簇
X, y = make_blobs(n_samples=10000, n_features=3, centers=[[3,3, 3], [0,0,0], [1,1,1], [2,2,2]], cluster_std=[0.2, 0.1, 0.2, 0.2],
random_state =9)
fig = plt.figure()
ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=30, azim=20)
plt.scatter(X[:, 0], X[:, 1], X[:, 2],marker='o')三维数据的分布图如下:
![]()
spss在因子分析应用
因子分析是一种数据简化的技术,通过研究众多变量之间的内部依赖关系,探求观测数据中的基本结构,并用少数几个假想变量来表示其基本的数据结构。
工具/原料
-
SPSS软件
-
数据
1.因子分析
-
1
1.因子分析
(1)主要思路:降维 简化数据结构
(2)目的:将(具有错综复杂关系的)变量 综合为 (数量较少的) 因子
以再现 原始变量与因子的关系, 通过不同的因子,对变量进行分类
消除 相关性,在信息损失最小的情况下,降维
(3)步骤
选取因子分析的变量(选相关性较大的,利于降维)――标准化处理;
根据样本、估计随机向量的协方差矩阵或相关矩阵;
选择一种方法――估计因子载荷阵,计算关键统计特征;
进行因子旋转,使因子含义清晰化,并命名,利用因子解释变量的构成;
计算每个因子在各样本上的得分,得出新的因子得分变量――进一步分析。
(4)如何分析
检验变量间偏相关度KMO值>0.6,才适合做因子分析;
调整因子个数,显示共同特征后即可命名。
-
2
2.因子分析操作步骤
-
3
3.看看结果吧
END
2.主成分分析
spss-因子分析/主成分分析-乳腺癌细胞
数据来源from sklearn.datasets import load_breast_cancer
KMO指数>0.8,说明变量相关性很强,适合因子分析或主成分分析
Bartlett的sig显著性为0,说明也OK,只是bartlett在某些场景参考意义不大
从方差解释来看,癌细胞受到6个因子共同决定,而非单一因素决定,和之前蒙特卡洛模拟结论一致
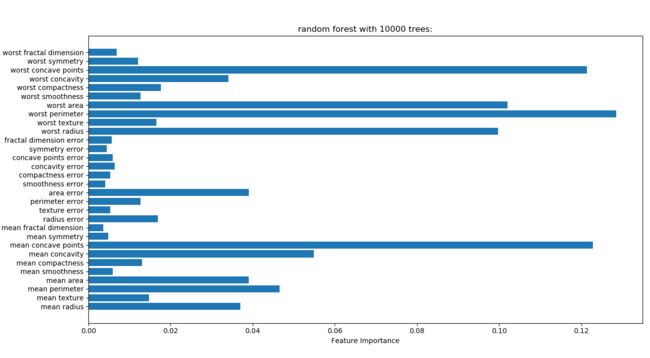
随机森林测试和因子分析的方差解释相差较大,随机森林更加准确,因子分析方差解释仅做参考
![]()
主成分图
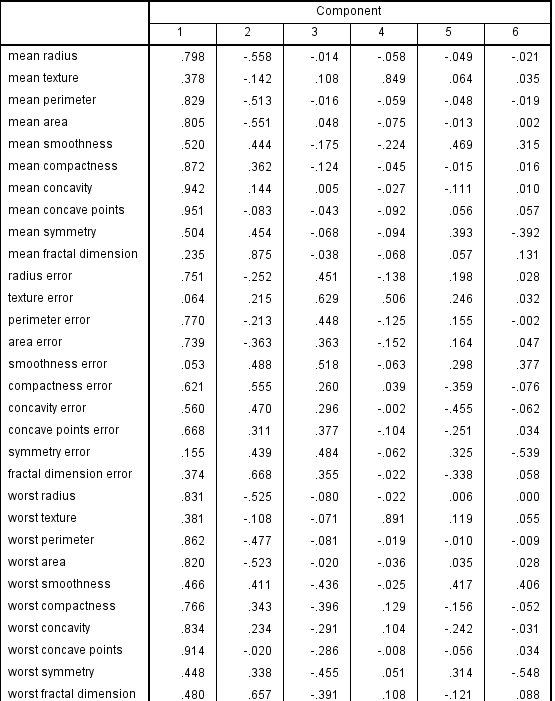
旋转后因子图,经过和主成分比较,旋转后因子成分变量参数很多大于0.9,比较显著,主成分中大于0.9的变量很少
Extraction Method: Principal Component Analysis.
Rotation Method: Varimax with Kaiser Normalization.
Rotation converged in 11 iterations.
因子总结结果:
随机森林测试结果,1000颗树
欢迎各位同学学习《python机器学习-乳腺癌细胞挖掘》课程,包含主成分分析和因子分析的python实战介绍,链接地址为