一种高超声速飞行器弹道的仿真方法

一种高超声速飞行器弹道的仿真方法

---

---

一、相关研究

临近空间高超声速飞行器（Near Space Hypersonic Vehicle, NSHV）飞行速度快、突防能力强、打击距离远，主要有 2 类: 一类是由火箭助推至大气层高空后，无动力再入大气层而长距离滑翔的升力式再入滑翔弹，典型的有 HTV-2 和AHW; 一类是机载平台投放后，由吸气式超燃冲压发动机连续启停助推的乘波体滑翔弹，典型的有X-43A、X-51A。

对高超声速飞行器的弹道特性进行仿真，可为高超声速飞行器的探测与拦截问题研究提供支撑；也可用于各种模拟系统，为其增加仿真对象和仿真样式。

文献[1]对X-51的试验过程与弹道特性进行了分析，但并未给出相应的计算模型。文献[2]将飞行器的飞行过程划分为高空巡航段和俯冲攻击段，在高空巡航段设计了常值稳态式、非周期性滑跃式和周期性跳跃式3种控制方案，在俯冲攻击段则采用比例导引法进行控制。文献[3]指出，高超声速滑翔飞行器具有两种典型的飞行弹道模式:一种称为平衡滑翔，最早由德国科学家 Saenger 于 20 世纪 30年代在研究高速升力式飞行时提出，其弹道特点是几乎没有波动的平坦滑翔下降弹道，近年来研究中把倾侧角时变条件的平衡滑翔称为准平衡滑翔;另一种是 Saenger 所设计的“银鸟”飞行器采用的滑翔跳跃弹道，即具有一定跳跃波动幅度的滑翔轨迹。该文献对纵向弹道特性进行了较为深入的分析。文献[4] 以升力式再入滑翔弹为对象，研究了控制量和初始运动状态对弹道轨迹的具体影响。文献[5]设计了以高度为节点约束、攻角为控制量的周期性跳跃巡航式制导飞行方案并生成弹道轨迹。文献[6]给出了常攻角飞行、常升阻比飞行、最优升阻比飞行、平衡滑翔飞行和横向机动的动力学模型。文献[7]给出了基于椭球的弹道仿真动力学模型。文献[8]则专门针对导弹爬升段建立了仿真模型。在飞行过程中为实现机动突防、过航路点或躲避禁飞区的目的，往往会选择适当的机动模式。高超声速目标典型的机动模式有纵向跳跃滑翔机动、侧向摆动突防机动以及螺旋机动等。文献[9]探讨了飞行器弹道中的机动特性，主要是目标的纵向和侧向机动能力。

---

二、基本思路

结合利用多个文献中给定模型，设计并实现了一个高超声速飞行器弹道仿真算法，并应用到基于OSGEarth的态势中。

在美飞行试验中，X-51A 由 B-52 轰炸机携带升空，自母机投放后经火箭推进至超燃冲压发动机的工作高度及飞行马赫数，然后超燃冲压发动机点火，将飞行器由马赫数 4.5 加速到马赫数 6 的巡航速度。

因此，主要仿真加速到6马赫之后的跳跃式飞行然后俯冲至目标的过程。即模型的输入输出如下
输入：发射点经度、纬度（高度限定为固定值，如20km）；目标点的经度、纬度、高度；
输出：飞行器弹道数据（采样点的位置矢量和速度矢量）。

滑翔和俯冲过程中需要各自独立的计算模型，但都需要求解微分方程，因此采用龙格库塔法求解。为提高方法的通用性，定义方程右值类为

class EquationRightCalculator{
	int	getNumOfEquation();
	void	getCurrentValue(double& t,double* y);	
	virtual void	setCurrentValue(double t,double* y);
	virtual void	calculate(double t,double* y,double* d)=0;
	int		_numOfEquation;
	double*	_currentY;
	double	_currentT;};

定义龙格库塔法类为

class RunghKutta{
	void	rk1();
	void	setStep(double step);
	double		getStep();
private:
	EquationRightCalculator*	_equationRightCalculator;
	double*	_y;
	double* _yTmp;
	double*	_d0, *_d1 , *_d2 , *_d3 ;
	double	_step;};

通过右值类指针，进行计算。

void	RunghKutta::rk1(){
	int n = _equationRightCalculator->getNumOfEquation();
	double t;
	_equationRightCalculator->getCurrentValue(t, _y);
	_equationRightCalculator->calculate(t, _y, _d0);
	for (int i = 0; i < n; i++)
		_yTmp[i] = _y[i] + _step / 2 * _d0[i];
	_equationRightCalculator->calculate(t+_step/2, _yTmp, _d1);
	for (int i = 0; i < n; i++)
		_yTmp[i] = _y[i] + _step / 2 * _d1[i];
	_equationRightCalculator->calculate(t + _step / 2, _yTmp, _d2);
	for (int i = 0; i < n; i++)
		_yTmp[i] = _y[i] + _step * _d2[i];
	_equationRightCalculator->calculate(t + _step , _yTmp, _d3);
	for (int i = 0; i < n; i++)
		_y[i] = _y[i] + _step / 6 * ( _d0[i] + 2 * _d1[i] + 2 * _d2[i] + _d3[i]);	
	_equationRightCalculator->setCurrentValue(t + _step, _y);}

在这种设计下，只要实现不同的右值计算类即可，而不必每次重写龙格库塔法的代码。

---

三、巡航段弹道计算

（1）动力学模型

V为飞行器速度；θ为航迹倾角；Ｄ为阻力；L为升力；Ｐ为发动机推力；α为攻角；φ为纬度；λ为经度；ψ为航迹方位角；σ为滚转角，不考虑滚转，其值设为0；ｇ为重力加速度；ｍ为飞行器质量。如推力P为0，则表示无动力滑翔段动力学模型。

实现上式右侧对应的右值类，即可进行计算。计算的变量为速度、航迹倾角、高度、经度、纬度、航迹方位角。计算过程中，需要攻角、航迹倾角、推力、升力、阻力、飞行器质量，用攻角和航迹倾角控制弹道生成（后续算法部分介绍），下面介绍升力、阻力和推力的计算。

（2）气动力模型

为使用动力学模型进行计算，需要获得升力L和阻力D，计算公式如下

式中：ρ为大气密度；ｓ为飞行器空气动力参考面积；C_D为阻力系数；C_L为升力系数；V为前面计算得到的速度。

大气密度计算采用文献[10]给出的公式计算

上述公式用于计算20~30km范围的大气密度，其中h为飞行高度，R为地球半径，ρ为大气密度。

通用乘波体的阻力系数与升力系数只随攻角变化，计算公式

其中攻角的范围在-10°至25°之间。

（3）推力计算

类X-51A在巡航段采用超燃冲压发动机提供推力，其燃料比冲的计算公式如下

式中M_a为飞行器马赫数。
假设发动机燃料消耗率不变，即飞行器的质量变化率不变，推力的计算公式为

其中,G_m为燃料消耗率，为常量，取0.5。

（4）周期性跳跃巡航弹道生成算法

每个周期分为4个阶段

如图所示，基于高度进行控制。控制飞行器的航迹倾角θ和攻角α，在每个高度给定航迹倾角和攻角，在使用龙格库塔法进行计算时，插值获得当前高度的航迹倾角和攻角。至此，动力学模型右值方程中所有变量均可产生，即可计算模型的位置和速度矢量。

在第1阶段，高度h₀至h₁，发动机点火，保持攻角不变，航迹倾角增加；第2阶段，高度h₁至h₂，关闭发动机，推力为0，攻角和航迹倾角都逐渐变化到0；第3阶段，高度h₂至h₃，继续进行滑翔，攻角和航迹倾角逐渐变化为负值；第4阶段，高度h₃至h₀，继续滑翔，攻角和航迹倾角变化为初始值。

上述控制过程并未考虑过载等各种约束，如果用于研究飞行器本身肯定是不够准确的，但用于仿真系统则基本满足。

---

四、俯冲段弹道计算

利用巡航段算法，每次生成一个周期数据后，判断与目标的距离，当与目标的距离在一个周期之内时，则进入俯冲段。进入俯冲段的位置是周期的最高点，即图中高度h2所对应位置，此时的速度矢量为水平方向，在俯冲过程中速度保持不变。

采用比例导引法求解。比例导引法是指导弹在攻击目标的过程中，导弹速度矢量的旋转角速度与目标线的旋转角速度成比例的一种导引方法。

由于打击目标位置固定，因此飞行器的相对运动方程组可简化如下

其中，r为飞行器相对目标的距离，q为目标线与基准线之间的夹角，称目标线方位角（目标线角），σ为飞行器速度矢量与基准线之间的夹角，称导弹弹道角，η为飞行器速度矢量与目标线之间的夹角，称为导弹速度矢量前置角。K为导引比例，取定值。

而对应的右值类计算代码为

void	X51GuidanceRightCalculator::calculate(double t, double* y, double* d){
	double frontAngle = y[TARGETAZIMITH] - y[HEADING];
	d[DISTANCE] = -_V * cos(frontAngle);
	d[TARGETAZIMITH] = _V * sin(frontAngle) / y[DISTANCE];
	d[HEADING] = _K * d[TARGETAZIMITH];}

根据目标位置、巡航弹道最后一个采样点位置建立坐标系，根据r、q值计算俯冲过程中每个采样点位置。

---

五、仿真结果

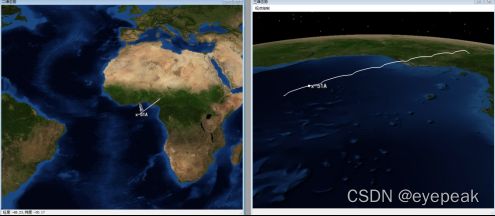
上图为飞行器弹道模拟的结果，经过6个完整的巡航周期，在第7个巡航周期顶点处开始俯冲。

上图为对应的由巡航转换到俯冲阶段放大观察的结果。

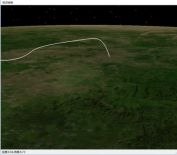
上图中目标位置改变，俯冲变得陡峭。

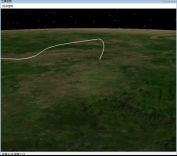
上图中巡航段顶点已经接近或略超过目标位置，俯冲时稍有回转。

---

参考文献

[1]张海林,周林,张琳,等. 临近空间高超声速导弹弹道特性分析[J].飞航导弹.2015(3):18-21.
[2]聂晓华,徐一鸣. 面向NSHV目标跟踪的飞行轨迹建模与仿真比较[J].计算机仿真,2016,33(3):41-46.
[3]李广华,张洪波,汤国建. 高超声速滑翔飞行器典型弹道特性分析[J].宇航学报,2015,36(4):397-403.
[4]喻晨龙,谭贤四,曲智国,等. 临近空间高超声速滑翔弹弹道特性仿真[J].装甲兵工程学院学报,2017,31(6):56-61.
[5]叶泽浩,毕红葵,段敏,等. 高超声速飞行器周期跳跃巡航轨迹设计与仿真[J].空军工程大学学报(自然科学版),2019,20(1):67-72.
[6]缪天宇. 助推滑翔式高超声速飞行器雷达探测与跟踪预报算法研究[D].哈尔滨:哈尔滨工业大学,2017,6:11-17.
[7]冯耀,王红,曲智国,等. 基于参考椭球的高超声速滑翔飞行器弹道仿真[J].计算机仿真,2020,37(10):18-23.
[8]冯绍东. 高超声速巡航导弹爬升段轨迹优化研究[D].长沙:国防科技大学,2017,11:11-27.
[9]陈文钰,邵雷,李万礼,等. 临近空间高超声速目标机动特性仿真研究[A].第21届系统仿真技术及其应用学术年会论文集[C]:143-147,
[10]杨炳尉.标准大气参数的公式表示[J].宇航学报,1983,4(1):83-86.