基于osgEarth的雷达作用范围绘制方法
文章目录
- 一、相关研究
- 二、雷达探测范围定义
- 三、雷达探测范围离散几何数据生成
- 四、雷达探测范围几何图元构造
- 五、效果
- 参考文献
一、相关研究
作为一种现代装备,雷达一直是一种重要的仿真对象,不论是各种雷达方程、资源调度、交接预报,以及结合弹道导弹目标的探测,结合预警卫星或置于大的探测体系中的分析都屡见不鲜。但可视化相关研究较少,多是作为某研究的附属出现。
可视化相关技术主要可分为5类:
①雷达模拟器。直接模拟雷达屏幕,根据雷达功能和目标特性,动态仿真雷达屏幕显示效果,可用于模拟训练等场合,如文献[1]采用软件实现了雷达模拟器,仿真雷达显示及参数设置与控制。
②示意性可视化。表现雷达作用的过程信息,作为态势的有机组成部分,如文献[2]设计了电磁特效对策类别、样式、颜色和参数,给出了几种典型的电磁对抗行动的显示效果。此项技术虽然简单,但是意义很重大,类似于标准、标号设计,如果得到认证和推广,会发挥比较大的作用。
③雷达威力切片可视化。这个概念未必合适,主要指2种情况:一是雷达天线方向图,对雷达系统仿真而言,雷达天线仿真是基础,如文献[3]进行了雷达天线方向图的建模,并给出了可视化结果;二是垂直面内雷达威力,以可视化方式展示某方位的雷达探测范围,如文献[4]采用C语言编程,绘制了垂直方向探测范围。
④雷达威力三维可视化。其实质是2个问题,探测威力数据如何生成、采取何种技术进行可视化。
文献[4]-[8]的探测范围数据生成技术基本类似,都是从雷达距离方程出发,考虑干扰等各种因素,生成表示探测范围的边界采样数据,然后进行绘制。文献[4]年代较为久远,绘制还较为简单;文献[5]采用三角形带绘制,未提及采用的具体平台;文献[6]、[7]出自同一团队,都是采用利用STK,将生成的威力数据作为数据文件导入的方式进行绘制;文献[8]则利用Direct3D进行绘制。
文献[3]和文献[9]在威力数据生成上的方法比较类似,都是采用离散化然后传递或跟踪的方法来计算边界。文献[3]采用OpenGL进行绘制。
此外,文献[10]在计算威力数据时考虑了地形的影响,文献[8]则将雷达探测范围可视化置于一个大的态势系统中实现。
⑤二维地图雷达威力可视化。虽然三维日益普及,但二维态势仍有其存在的价值,在二维地图上显示雷达探测范围也有其固有的应用领域,也有需要解决的技术细节。
二、雷达探测范围定义
采用OSGEarth开发平台,雷达探测范围是已经计算出来的结果,其表达形式定义如下。
class RadarRange{
cartesianFrame _frame; //坐标系
double _minRange; //最小作用距离,单位为m,
double _maxRange; //最大作用距离,单位为m
double _minAzimuthAngle; //方位角,与x轴夹角,单位是度,由-180°~180°
double _maxAzimuthAngle;
double _minElevetionAngle; //仰角,0°-90°
double _maxElevetionAngle;}
显然,这样的定义方式并不足以描述干扰、地形等各种影响,但对于并非装备级的仿真和态势系统来说,是可以的。
cartesianFrame用于表达坐标系,采用原点和三个坐标轴表示。
class cartesianFrame{
private:
CVector3D _origin;
CVector3D _xAxis;
CVector3D _yAxis;
CVector3D _zAxis;};
给定经纬度和高程,生成该位置的雷达直角坐标系如下
void cartesianFrame::initENUFrame(double B, double L, double H){
double sb = B * PI / 180.0;
double sl = L * PI / 180.0;
_yAxis.x = -sin(sb)*cos(sl);
_yAxis.y = -sin(sb)*sin(sl);
_yAxis.z = cos(sb);
_yAxis.SetUnit();
_xAxis.x = -sin(sl);
_xAxis.y = cos(sl);
_xAxis.z = 0.0;
_xAxis.SetUnit();
_zAxis.x = cos(sb)*cos(sl);
_zAxis.y = cos(sb)*sin(sl);
_zAxis.z = sin(sb);
_zAxis.SetUnit();
LB2DD(B, L, H, _origin.x, _origin.y, _origin.z);
三、雷达探测范围离散几何数据生成
根据上述定义可知,雷达探测范围在垂直方向的二维图如下

为了绘制雷达探测范围,生成离散的采样点,然后构造几何图元即可。
根据上述形状,显然,可以生成前、后两个曲面上的离散点,顶面、底面和侧面则可以直接利用曲面的边界上点绘制。
采用的方法是在方位、俯仰两个方向上,每隔1度生成一个采样点。
osg::ref_ptr<osg::Vec3Array> va = dynamic_cast<osg::Vec3Array*>(_radarGeometry->getVertexArray());
va->resize(_xDim*_yDim * 2+2);
for (int i = 0; i < _yDim; i++){
for (int j = 0; j < _xDim; j++){
double xa = (_radarWorkingMode->_minAzimuthAngle + xDelta * j) ;
double ya = (_radarWorkingMode->_minElevetionAngle + yDelta * i) ;
CPoint3D v2 = _radarWorkingMode->_frame.getGloballCoordFromAzElRa(xa, ya, _radarWorkingMode->_minRange);
(*va)[i*_xDim + j] = osg::Vec3d(v2.x, v2.y, v2.z);
v2 = _radarWorkingMode->_frame.getGloballCoordFromAzElRa(xa, ya, _radarWorkingMode->_maxRange * scale);
(*va)[i*_xDim + j + _xDim * _yDim] = osg::Vec3d(v2.x, v2.y, v2.z);}}
(*va)[_xDim*_yDim * 2+1] = osg::Vec3d(0, 0, 0);
其中,根据方位角、俯仰角和距离生成雷达坐标系中点矢量的代码如下
CPoint3D cartesianFrame::getGloballCoordFromAzElRa(double az, double el,double ra){
double cosAz = cos(az*PI / 180.0);
double sinAz = sin(az*PI / 180.0);
double cosEl = cos(el*PI / 180.0);
double sinEl = sin(el*PI / 180.0);
double y = ra * cosEl*cosAz;
double x = ra * cosEl * sinAz;
double z = ra * sinEl;
CPoint3D pos = _origin + _xAxis * x + _yAxis * y + _zAxis * z;
return pos;}
近曲面和远曲面的数据分别存储,最后存储的数据用于图元重启。
四、雷达探测范围几何图元构造

生成的数据是类似于上图中的离散网格点,为了表现雷达探测范围,采用索引形式构造图元,同时需要使用图元重启技术。
osg::ref_ptr<osg::DrawElementsUShort> _radarPlaneElements;
osg::ref_ptr<osg::DrawElementsUShort> _radarLineElements;
osg::ref_ptr<osg::DrawElementsUShort> _radarLineStripeElements;
osg::ref_ptr<osg::Geometry> _radarGeometry;
采用了三个图元,radarPlaneElements以具有半透明效果的面表示雷达范围。
radarLineElements和radarLineStripeElements是用于表示雷达范围的网格线,用于增强三维效果,其中前者用于表示上、下、左、右面中的线;后者用于表示前、后曲面的线。
如前面曲面图元的构造如下
for (int i = 0; i < _yDim - 1; i++){
for (int j = 0; j < _xDim; j++){
_radarPlaneElements->push_back(j + i * _xDim);
_radarPlaneElements->push_back(j + (i + 1) * _xDim);}
_radarPlaneElements->push_back(restartindex); }
tmp = _yDim / _lineInterval;
off = (double)(_yDim) / tmp;
for (int i = 0; i <= tmp; i++){
double tmp1 = off * i;
int pos = int(tmp1);
if (pos >= _yDim)pos = _yDim - 1;
for (int j = 0; j < _xDim; j++)
_radarLineStripeElements->push_back(j + pos * _xDim);
_radarLineStripeElements->push_back(restartindex);}
tmp = _xDim / _lineInterval;
off = (double)(_xDim) / tmp;
for (int i = 0; i <= tmp; i++){
double tmp1 = off * i;
int pos = int(tmp1);
if (pos >= _xDim)
pos = _xDim - 1;
for (int j = 0; j < _yDim; j++)
_radarLineStripeElements->push_back(j * _xDim + pos);
_radarLineStripeElements->push_back(restartindex);}
上方平面图元的构造如下
for (int i = 0; i < _xDim; i++){
int pos = _xDim * (_yDim - 1) + i;
_radarPlaneElements->push_back(pos);
_radarPlaneElements->push_back(pos + _xDim * _yDim);}
_radarPlaneElements->push_back(restartindex);
tmp = _xDim / _lineInterval;
off = (double)(_xDim) / tmp;
for (int i = 0; i <= tmp; i++){
double tmp1 = off * i;
int pos = int(tmp1);
if (pos >= _xDim)pos = _xDim - 1;
_radarLineElements->push_back(_xDim * (_yDim - 1) + pos);
_radarLineElements->push_back(_xDim*_yDim + _xDim * (_yDim - 1) + pos);}
_radarLineElements->push_back(restartindex);
其余4个面也类似,分别构造。
五、效果

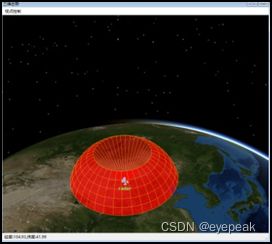
上图中,雷达方位角范围120°,最小仰角15°,最大仰角60°,最近最远距离为100km和1000km。
上图中表示全向雷达,方位角范围360°。
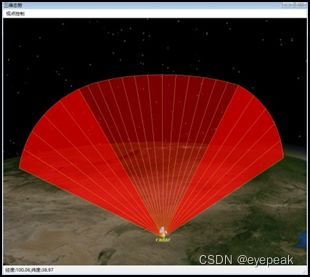
上图中雷达的最小距离为0。
需要指出的是,由于表示雷达的图元是按固定顺序构造的,而透明物体不写入z缓存将导致显示效果会随着视点而出现问题(博文《基于osgEarth的卫星瞬时覆盖绘制方法》),区别在于卫星圆锥覆盖是凸的,当采用Z缓存消隐加背面剔除时覆盖面肯定是正常的,改进是锦上添花,但是雷达范围本身较为复杂,即使采用了上述技术,覆盖面显示仍然会出现不稳定。下一步将解决此问题。
参考文献
[1] 朱保安,何东越,徐成前,等.雷达模拟器设计与实现[J].电脑知识与技术,2022,18(20):115-117.
[2] 陈行勇,马启原.基于动画特效的电磁态势显控方法[J].电子信息对抗技术,2022,37(3):91-94.
[3] 冯晓哲,杨瑞,王健,等. 雷达探测威力范围与三维可视化研究[J].现代雷达,2015,37(5):74-78.
[4] 张尉,程柏林,刘素华.搜索雷达探测范围的可视化技术[J].现代雷达,2000,22(4):43-47.
[5] 陈鹏,孟国明,吴玲达.虚拟战场环境中雷达作用范围表现技术研究[J].北京理工大学学报,2006,26(26S):57-60.
[6] 徐鹏,王振华,刘东青,等. 基于STK的雷达威力三维可视化仿真方法[J]. 空军预警学院学报,2018,32(2):114-117.
[7] 刘东青,王振华,彭赛阳.基于STK平台下的雷达干扰可视化仿真分析[J]. 空军预警学院学报,2017,31(5):360-364.
[8] 陈弓,戴晨光,刘航冶.雷达阵地场景三维可视化系统的研究与实现[J].计算机仿真,2008,25(9):227-230.
[9] 杨超,陈鹏,魏迎梅.雷达最大探测范围三维可视化研究与实现[J]. 计算机工程与应用,2007,43(11):245-248.
[10] 邱航,陈雷霆.地形影响下雷达作用范围三维可视化研究[J]. 电子测量与仪器学报,2010,24(6):528-535.