雷达作用范围的二维绘制方法

---

尽管三维态势方兴未艾，但二维表现形式仍然具有非常重要的地位和作用。在各种形式的二维地图上，表现雷达探测范围，有利于精确表示和测量雷达探测的地理信息。但由于探测范围本身是三维的，因此如何用二维方式进行表示还需要设计，并构造其实现方法；由于二维的地图存在投影形变，因此在表现范围时需要特殊处理，这可以通过离散化的方式进行；对于多部雷达，需要表示其总的范围，这涉及多部雷达包络的求取。

---

一、雷达探测范围二维表现形式设计

雷达威力范围的定义参见 博文《基于osgEarth的雷达作用范围绘制方法》 。

根据参数的不同，雷达的二维形状可能如下（投影后会变形），分别定义为Fan，FanCap，CircleWithoutHole，CircleWithHole。不同类型采用不同的绘制方法，如Fan和CircleWithoutHole采用三角形扇，FanCap和CircleWithHole采用三角形带。CircleWithHole类型由于存在内环，在后续计算包络的处理也不同。

二维绘制仍然采用离散化技术，需要计算上述形状的边界点，这需要根据垂直方向切面进行设计。

雷达垂直方向切面如图所示。

设计了3种二维范围表示方式。

①最近最远距离，即图中a、b所代表的距离，分别是雷达探测的最近和最远距离。显然，这是探测能力的示意，因为在这样一个范围内（二维映射到三维后）是存在一些区域，在二维图上位于区域之内，但实际在区域之外。

②基于雷达坐标系高度。给定雷达坐标系高度，计算探测范围在该高度上的截面。如图中c、d所代表的范围。这可以用于判断在雷达坐标系某高度上对目标的探测能力。

③基于给定高程。给定高程，计算该高程上的探测范围，由于地球表面为曲面，因此高程与雷达坐标系高度也并不相同，如图中e、f所表示的范围。此种方式应该较为实用，在已知目标飞行高度的情况下，可分析雷达的探测能力。

---

二、雷达二维探测范围计算

1.基于最近最远距离的雷达探测范围

最近距离的采样点，利用最小探测距离和最大仰角得到，最远距离采样点，利用最大探测距离和最小仰角得到。

for (int i = 0; i <= xDim; i++){
double xa = (_minAzimuthAngle + xDelta * i) ;
	double ya = _minElevetionAngle ;
	CPoint3D pos = _frame.getGeotedicCoordFromAzElRa(xa,ya, _maxRangeLow * scale);
	loop.push_back(CPoint2D(pos.x, pos.y));}
	if (fabs(_minRange) >= 10)	{
		for (int i = xDim ; i >= 0; i--){
			double xa = (_minAzimuthAngle + xDelta * i) ;
			double ya = _maxElevetionAngle ;
			CPoint3D pos = _frame.getGeotedicCoordFromAzElRa(xa, ya, nearRa);
				loop.push_back(CPoint2D(pos.x, pos.y));}}
	if (fabs(fabs(_maxAzimuthAngle - _minAzimuthAngle) - 360) < 1e-5){
		if (fabs(nearRa) < 10)	return  CircleWithoutHole;
		else	return  CircleWithHole;}
	else{
		if (fabs(nearRa) < 10){
			CVector3D v0(0, 0, 0);
			CVector3D v2 = _frame.frame2World(v0);
			double L, B, H;
			DD2LB(v2.x, v2.y, v2.z, B, L, H);
			loop.push_back(CPoint2D(L, B));
			return Fan;}
		else	return FanCap;}

2.给定雷达坐标系高度的雷达探测范围

此种方式和高程方式，探测区域一定是形成FanCap或者 CircleWithHole，而不可能是Fan或CircleWithoutHole。计算时，可以分别计算外圈采样点和内圈采样点，然后把两者组合起来。如果是全向天线，则会形成带内环的CircleWithHole，否则形成FanCap。

如图所示，垂直方向上四个边界点a、b、c、d的高度分别为h0、h1、h2、h3，其值可以利用雷达探测范围的最小最大距离和最小最大俯仰角计算得到。其中h0最低，h2最高，h1和h3二者存在互有高低的可能。

其中，ab段和bc段，所生成的一定是外圈数据，cd段和da段，所生成的一定是内圈数据。

根据给定高度，可以判断是否落在某一段，然后计算在该段的交点，得到采样点。

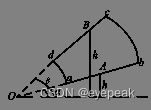
对于ab段和cd段的情况，如图所示，其计算相对简单：计算出OA或OB的长度，然后按第一种最近最远距离的方法计算即可。而OA或OB的长度显然通过给定高度h除以俯仰角的反正弦值即可得到。

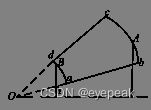
对于bc段和da段的情况，如图所示，通过数值方法计算：以最大最小俯仰角度作为控制值，记为e0和e1；取2个俯仰角的中值em，计算对应的高度l；如果l和h的误差在给定阈值之内，则终止循环；如果l>h，则e1=em，否则e0=em，继续循环。

3.给定高程的雷达探测范围

给定高程来计算雷达探测范围，在上图ab、bc、cd、da4个段中，均需采用二分查找的数值计算方法。

QVector<CPoint2D> loop1;//存储内圈数据
for (int i = 0; i <= xDim; i++){
	double xa = (minAz + xDelta * i) ;
	double ya0 = minEl ;
	double ya1 = maxEl ;
	double ra0 = minRange;
	double ra1 = maxRangeLow;
	double ra2 = maxRangeHigh;
	double L, B;
	bool flag = calculateBorderOuter(h, xa, ra1, ra2, ya0, ya1, L, B);//外边界
	if (!flag)flag = calculateBorderTopBottom(h, xa, ya0, ra0, ra1, L, B);//下边界
	if (!flag)return NoShape;
	loop.push_back(CPoint2D(L, B));	
	flag = calculateBorderTopBottom(h, xa, ya1, ra0, ra2, L, B);	//上边界
	if (!flag)flag = calculateBorderInner(h, xa, ra0, ya0, ya1, L, B);//内边界
	if (!flag)return NoShape;
	loop1.push_back(CPoint2D(L, B));}
	for (int i = loop1.size() - 1; i >= 0; i--)loop.push_back(loop1.at(i));
	if (fabs(fabs(_maxAzimuthAngle - _minAzimuthAngle) - 360) < 1e-5)	
		return CircleWithHole;
	else	return FanCap;

其中的calculateBorderOuter用于计算外边界bc段上的给定高程点，以俯仰角控制迭代。

bool	ConicFrustum::calculateBorderOuter(double altitude, double az, double ra0, double ra1, double el0, double el1, double& L, double& B){
	CPoint3D p0 = _frame.getGeotedicCoordFromAzElRa(az, el0, ra0);
	if ( p0.z > altitude)	return false;
	p0 = _frame.getGeotedicCoordFromAzElRa(az, el1, ra1);
	if (p0.z < altitude)	return false;	
	while (true){
		double elm = (el0 + el1) / 2;
		double se = (elm - el0) / (el1 - el0);
		double ra = ra0 + (ra1 - ra0) * se;
		p0 = _frame.getGeotedicCoordFromAzElRa(az, elm, ra);
		if (fabs(p0.z - altitude) < 0.1)break;
		if ( p0.z < altitude)el0 = elm;
		else	el1 = elm;
		if (fabs(el1 - el0) < 1e-5)break;}
	L = p0.x;
	B = p0.y;
	return true;}

calculateBorderTopBottom用于计算上、下边界（ab段和cd段）给定高程点，以距离控制迭代。

bool	ConicFrustum::calculateBorderTopBottom(double altitude, double az, double el, double ra0, double ra1, double& L, double& B){
	CPoint3D p0 = _frame.getGeotedicCoordFromAzElRa(az, el, ra0);
	if (p0.z > altitude)return false;
	p0 = _frame.getGeotedicCoordFromAzElRa(az, el, ra1);
if (p0.z < altitude)	return false;
	while (true){
		double ram = (ra0 + ra1) / 2;
		p0 = _frame.getGeotedicCoordFromAzElRa(az, el, ram);
		if (fabs(p0.z - altitude) < 0.1)break;
		if (p0.z < altitude)ra0 = ram;
		else	ra1 = ram;
		if (fabs(ra1 - ra0) < 0.1)break;}
	L = p0.x;
	B = p0.y;
	return true;}

4.绘制效果

下面给出一些绘制结果。

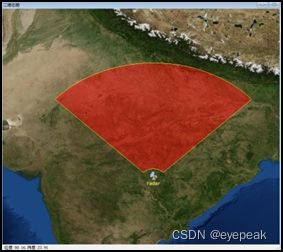
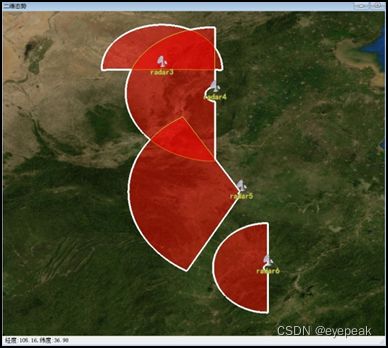
上图为一雷达二维覆盖，其俯仰角为15-60°，方位角范围90°，最近探测距离200km，最大探测距离1000km。形成的类型为FanCap，采用的二维范围显示方式为最近最远距离。

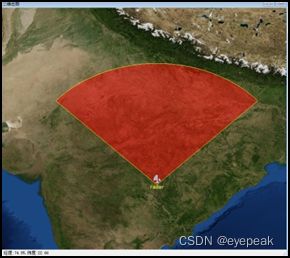
上图的最近探测距离为0。形成的类型为Fan。

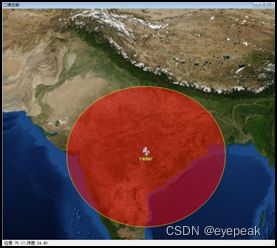
上图中方位角范围360°，全向天线。形成类型CircleWithoutHole。

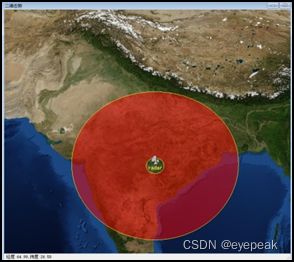
上图中将最小探测距离重新设置为200km，形成类型CircleWithHole，带内环。

上图中二维显示方式为基于雷达坐标系高度，给定高度100km，其探测范围远小于最近最远距离方式，外圈收缩，内圈外扩。

基于高程的显示方式，范围比基于雷达坐标系高度会更小一些，外圈进一步收缩，内圈进一步外扩。由于不是特别显著，此处不再附图。

以上各图，由于雷达部署纬度较低，因此投影变形不明显，近似为圆。同样的雷达，部署在高纬的二维覆盖如下图所示。

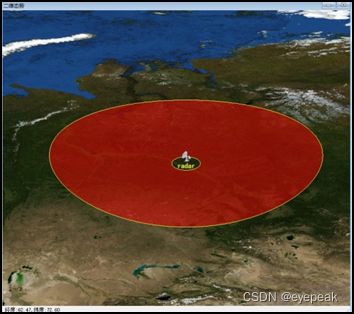
三、基于GEOS的雷达包络计算

显然，多部雷达的二维包络可通过各雷达二维覆盖的多边形并运算得到。为此采用GEOS库。

1.GEOS库及其简单封装

GEOS是一个开源的计算几何库，以C语言形式提供了接口。为便于使用，稍作封装，采用singleton设计模式，将库的初始化等工作隐藏起来，实现自定义数据格式的转换。自定义的多边形采用二维点数组的数组表示，数组中只有一个点集，为一个多边形，有多个点集，第一个为外环，其他为内环。前述Fan，FanCap，CircleWithoutHole，CircleWithHole，只有最后一种带内环。

typedef QVector<CPoint2D> LoopPts;
class geosLib{
public:
	static  geosLib*  getInstance();
	int     splitPolygons(GEOSGeometry* geom, QVector<GEOSGeometry*>& polygons);
	GEOSGeometry*   createGEOSPolygon(QVector<LoopPts>& loops);
	int		getPolygonNum(const GEOSGeometry* geom);
	bool	getPolygonLoops(const GEOSGeometry* geom,int index, QVector<LoopPts>& loops);	
	void    releaseGEOSPolygon(GEOSGeometry* poly);
	int     createLoop(GEOSGeometry* geom, QVector<LoopPts>& loops);
	GEOSGeometry*   createGEOSPolygon(const QVector<CPoint2D>& loop);
private:
	static  geosLib* _geosLib;
	geosLib();
	~geosLib();};

2.多边形union操作计算雷达覆盖包络

有了GEOS之后，计算雷达覆盖包络非常简单。

GEOSGeometry* geom = 0 ;
for (int i = 0; i < Application::_phasedArrayRadars.size(); i++){
	PhasedArrayRadar* radar = Application::_phasedArrayRadars.at(i);
	QVector<Loop2D> loops;
	radar->generateGeomtryData2D(loops);
	for (int j = 0; j < loops.size(); j ++){
		QVector<Loop2D> loops1;
		loops1.clear();
		loops1.push_back(loops.at(j));
		if (geom == 0)geom = geosLib::getInstance()->createGEOSPolygon(loops1);
		else{
			GEOSGeometry* geom1 = geosLib::getInstance()->createGEOSPolygon(loops1);
			GEOSGeometry* geom2 = GEOSUnion(geom, geom1);
			geom = geom2;}}}
int num = geosLib::getInstance()->getPolygonNum(geom);
GeoExtent extent(SpatialReference::create("wgs84"), -180, -90, 180, 90);
const SpatialReference* featureSRS = extent.getSRS();
const SpatialReference* outputSRS = Application::_mapNode2D->getMap()->getSRS();

osg::ref_ptr<osg::Geode> geode = new osg::Geode(); 
for (int i = 0; i < num; i++)	{
	QVector<LoopPts> loops;
	geosLib::getInstance()->getPolygonLoops(geom,i, loops);
	std::vector<osg::Vec3d> pts0;
	for (int j = 0; j < loops.size(); j++)	{
		pts0.clear();
		for (int k = 0; k < loops.at(j).size(); k++)
			pts0.push_back(osg::Vec3d(loops.at(j).at(k).x, loops.at(j).at(k).y, 0));
		featureSRS->transform(pts0, outputSRS);
		加入OSG geometry对象;}

3.包络绘制效果

雷达覆盖包络显示效果如图所示，包络线加粗绘制。