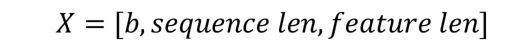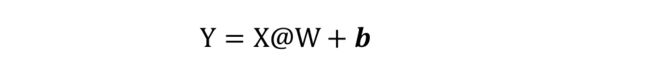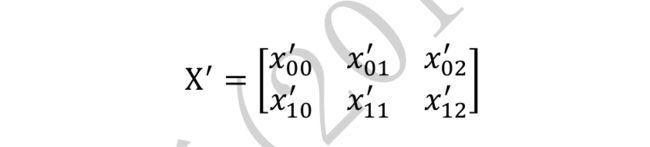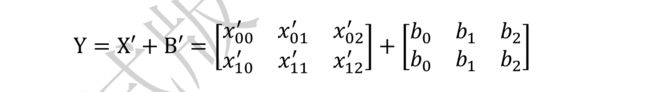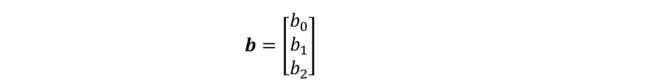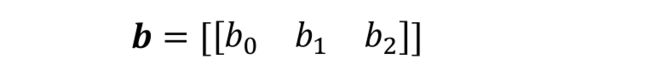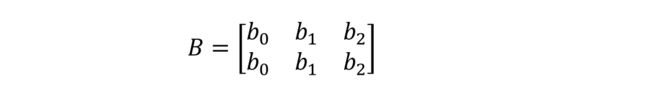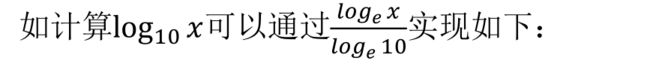tensorflow2深度学习从入门到精通第四章—TensorFlow 基础
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6FgLmduo-1651546929799)(https://i 《大厂前端面试题解析+Web核心总结学习笔记+企业项目实战源码+最新高清讲解视频》无偿开源 徽信搜索公众号【编程进阶路】 mg-blog.csdnimg.cn/20201208160045815.png#pic_center)]
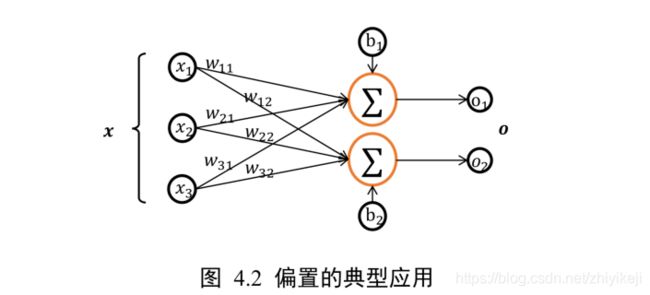
可以看到,类的偏置成员 bias 初始化为全 0,这也是偏置的默认初始化方案。
[](()4.5.3 矩阵
矩阵也是非常常见的张量类型,比如全连接层的批量输入![]()
,其中b表示输入样本的个数,即 batch size, d i n d_in din表示输入特征的长度。
比如特征长度为 4,一共包含 2 个样本的输入可以表示为矩阵:
x = tf.random.normal([2,4])
令全连接层的输出节点数为 3,则它的权值张量 W 的 shape 为[4,3]:
x = tf.random.normal([2, 4])
w = tf.ones([4, 3]) # 定义w张量
b = tf.zeros([3]) # 定义b张量
o = x @ w + b # x@w+b运算 @ 等价于tf.matmul表示矩阵相乘
print(o)
下面解释几行代码
- o = x @ w + b
@ 等价于tf.matmul表示矩阵相乘
其中 X,W 张量均是矩阵。x@w+b 网络层称为线性层,在 TensorFlow 中可以通过 Dense类直接实现,Dense 层也称为全连接层。
写到此处解释一下全连接层
![]()
最后的两列小圆球就是两个全连接层,在最后一层卷积结束后,进行了最后一次池化,输出了20个12_12的图像,然后通过了一个全连接层变成了1_100的向量。
我们通过 Dense 类创建输入 4 个节点,输出 3 个节点的网络层,可以通过全连接层的 kernel 成员名查看其权值矩阵 W:
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
fc=layers.Dense(3) #定义全连接层的输出节点为3
fc.build(input_shape=(2,4)) #定义全连接层的输入节点为4
print(“fc.kernel:”,fc.kernel)
[](()4.5.4 3 维张量
三维的张量一个典型应用是表示序列信号,它的格式是
-
b表示序列信号的数量
-
sequence len 表示序列信号在时间维度上的采样点数
-
feature len 表示每个点的特征长度。
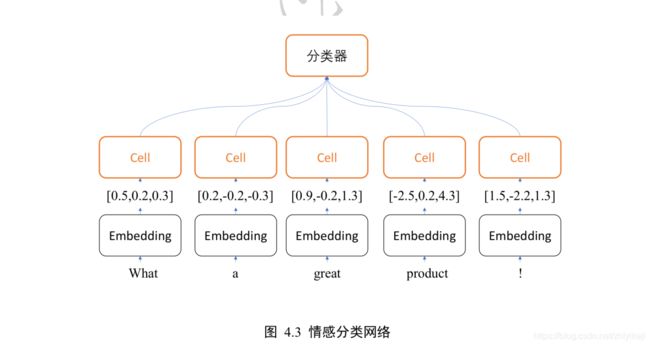
如图 4.3 所示。为了能够方便字符串被神经网络处理,一般将单词通过嵌入层(Embedding Layer)编码为固定长度的向量,比如“a”编码为某个长度 3 的向量,那么 2 个等长(单词数为 5)的句子序列可以表示为 shape 为[2,5,3]的 3 维张量,其中 2 表示句子个数,5 表示单词数量,3 表示单词向量的长度
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
(x_train, y_train), (x_test, y_test) = keras.datasets.imdb.load_data(num_words=10000) # 自动加载 IMDB 电影评价数据集
x_train = keras.preprocessing.sequence.pad_sequences(x_train, maxlen=80) # 将句子填充、截断为等长 80 个单词的句子
print(x_train.shape)
embedding = layers.Embedding(10000, 100) # 创建词向量 Embedding 层类
out = embedding(x_train) # 将数字编码的单词转换为词向量
print(out.shape)
可以看到,经过 Embedding 层编码后,句子张量的 shape 变为[25000,80,100],其中 100 表示每个单词编码为长度 100 的向量
对于特征长度为 1 的序列信号,比如商品价格在 60 天内即可表示商品的价格,因此 2 件商品的价格变化趋势可以使用 shape 为[2,60]的张量表示。为了方便统一格式,也将价格变化趋势表达为 shape 为 [2,60,1]的张量,其中的 1 表示特征长度为 1
[](()4.5.5 4 维张量
4 维张量在卷积神经网络中应用的非常广泛,它用于保存特征图(Feature maps)数据,格式一般定义为 [ b , h , w , c ] [b,h,w,c] [b,h,w,c]
-
b表示输入的数量
-
h/w:特征图的宽高
-
c:特征图的通道数
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
x = tf.random.normal([4, 32, 32, 3]) # 创建32*32的彩色图片,个数为4
layer = layers.Conv2D(16, kernel_size=3) # 创建卷积神经网络
out = layer(x) # 前向计算
print(out.shape) # 计算输出大小
print(layer.kernel.shape) # 卷积核张量也是 4 维张量,可以通过 kernel 成员变量访问
[](()4.6 索引与切片
通过索引与切片操作可以提取张量的部分数据,使用频率非常高。
[](()4.6.1 索引
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
x = tf.random.normal([4, 32, 32, 3])
print(“第一张图片的数据”, x[0])
print(“第一张图片的第二行数据:”, x[0][1])
print(“第一张图片的第二行第三列的像素:”, x[0][1][2])
print(“取第 3 张图片,第 2 行,第 1 列的像素,B 通道(第 2 个通道)颜色强度值:”, x[2][1][0][1])
当张量的维度数较高时,使用[][]…[]的方式书写不方便,可以采用[,,…,]的方式索引,它们是等价的。
print(“取第 2 张图片,第 10 行,第 3 列:”,x[1,9,2])
![]()
[](()4.6.2 切片
通过start : end:step切片方式可以方便地提取一段数据
-
start 为开始读取位置的索引
-
end 为结束读取位置的索引(不包含 end 位)
-
step 为读取步长
以 shape 为[4,32,32,3]的图片张量为例:
print(“读取第 2,3 张图片:”,x[1:3])
如 x[0,::]表示读取第 1 张图片的所有行,其中::表示在行维度上读取所有行,它等于x[0]的写法
print(“读取第 1 张图片的所有行:”, x[0,::])
我们来总结start : end:step切片的简写方式,其中从第一个元素读取时 start 可以省略,即 start=0 是可以省略,取到最后一个元素时 end 可以省略,步长为 1 时 step 可以省略,简写方式总结如表格 4.1:
特别地,step 可以为负数,考虑最特殊的一种例子,step = −1时,start : end:−1表示从 start 开始,逆序读取至 end 结束(不包含 end),索引号end<=start
x = tf.range(9)
print(“x:”, x)
print(“x[8:0:-1]”, x[8:0:-1])
print(“逆序取全部元素:”,x[::-1])
print(“逆序间隔采样:”,x[::-2])
当张量的维度数量较多时,不需要采样的维度一般用单冒号:表示采样所有元素,此时有可能出现大量的:出现
我们继续考虑[4,32,32,3]的图片张量,当需要读取 G 通道上的数据时,前面所有维度全部提取,此时需要写为:
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
x = tf.random.normal([4, 32, 32, 3])
print(x[:, :, :, 1])
为了避免出现像x[:,:,:,1]这样出现过多冒号的情况,可以使用⋯符号表示取多个维度上所有的数据,其中维度的数量需根据规则自动推断:当切片方式出现⋯符号时,⋯符号,左边的维度将自动对齐到最左边,⋯符号右边的维度将自动对齐到最右边,此时系统再自动推断⋯符号代表的维度数量,它的切片方式总结如表格4.2
比如读取第 1-2 张图片的 G/B 通道数据:
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
x = tf.random.normal([4, 32, 32, 3])
print(“读取第 1-2 张图片的 G/B 通道数据:”,x[0:2,…,1:])
读取最后 2 张图片:
x = tf.random.normal([4, 32, 32, 3])
print(“读取最后 2 张图片:”, x[2:,…])
读取 R/G 通道数据:
print(“读取最后 2 张图片:”, x[2:, …])
[](()4.6.3 小结
张量的索引与切片方式多种多样,尤其是切片操作,初学者容易犯迷糊。但其实本质上切片操作只有start : end : step这一种基本形式,通过这种基本形式有目的地省略掉默认参数,从而衍生出多种简写方法,这也是很好理解的。它衍生的简写形式熟练后一看就能推测出省略掉的信息,书写起来也更方便快捷。由于深度学习一般处理的维度数在 4 维以内,⋯操作符完全可以用:符号代替,因此理解了这些就会发现张量切片操作并不复杂。
[](()4.7 维度变换
在神经网络运算过程中,维度变换是最核心的张量操作,通过维度变换可以将数据任意地切换形式,满足不同场合的运算需求。
那么为什么需要维度变换呢?考虑线性层的批量形式:
其中 X 包含了 2 个样本,每个样本的特征长度为 4,X 的 shape 为[2,4]。线性层的输出为3个节点,即 W 的 shape 定义为[4,3],偏置的 shape 定义为[3]。那么X@W的运算张量shape 为[2,3],需要叠加上 shape 为[3]的偏置。
对于 2 个样本的输入 X,我们需要将 shape 为[3]的偏置
b = [ b 0 b 1 b 2 ] (2) b= \left[ \begin{matrix} b0 \\ b1 \\ b2 \end{matrix} \right]\tag{2} b=⎣⎡b0b1b2⎦⎤(2)
按样本数量复制 1 份,变成矩阵形式 ′ :
B ′ = [ b 0 b 1 b 2 b 0 b 1 b 2 ] (2) B’= \left[ \begin{matrix} b0 & b1 & b2 \\ b0 & b1 & b2 \\ \end{matrix} \right]\tag{2} B′=[b0b0b1b1b2b2](2)
通过与X′ = X@W
相加,此时X′与 ′ shape 相同,满足矩阵相加的数学条件:
通过这种方式,既满足了数学上矩阵相加需要 shape 一致的条件,又达到了给每个输入样本的输出节共享偏置的逻辑。
为了实现这种运算方式,我们将插入一个新的维度,并把它定义为 batch 维度,然后在 batch 维度将数据复制 1 份,得到变换后的B′,新的 shape 为[2,3]
[](()4.7.1 Reshape
在介绍改变视图操作之前,我们先来认识一下张量的存储和视图(View)的概念
- 张量的视图:就是我们理解张量的方式
比如 shape 为[2,4,4,3]的张量 A,我们从逻辑上可以理解为 2 张图片,每张图片 4 行 4 列,每个位置有 RGB 3 个通道的数据
- 张量的存储:张量在内存上保存为一段连续的内存区域,对于同样的存储,我们可以有不同的理解方式
比如上述 A,我们可以在不改变张量的存储下,将张量 A 理解为 2 个样本,每个样本的特征为长度 48 的向量。这就是存储与视图的关系。
我们通过 tf.range()模拟生成 x 的数据:
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
x=tf.range(96)
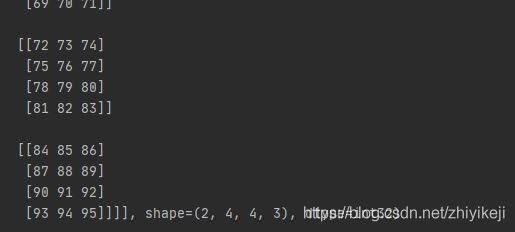
x=tf.reshape(x,[2,4,4,3])
print(x)
在存储数据时,内存并不支持这个维度层级概念,只能以平铺方式按序写入内存,因此这种层级关系需要人为管理,也就是说,每个张量的存储顺序需要人为跟踪。
为了方便表达,我们把张量 shape 中相对靠左侧的维度叫做大维度,shape 中相对靠右侧的维度叫做小维度
比如[2,4,4,3]的张量中,图片数量维度与通道数量相比,图片数量叫做大维度,通道数叫做小维度。在优先写入小维度的设定下,上述张量的内存布局为
数据在创建时按着初始的维度顺序写入,改变张量的视图仅仅是改变了张量的理解方式,并不会改变张量的存储顺序,这在一定程度上是从计算效率考虑的,大量数据的写入操作会消耗较多的计算资源。
改变视图操作在提供便捷性的同时,也会带来很多逻辑隐患,这主要的原因是张量的视图与存储不同步造成的。
我们先介绍合法的视图变换操作,再介绍不合法的视图变换。
比如张量按着初始视图[b,h,w,c]写入的内存布局,我们改变初始视图[b,h,w,c]的理解方式,它可以有多种合法理解方式:
-
[b,h*w,c ] 张量理解为 b 张图片,h * w 个像素点,c 个通道
-
[b,h,w * c ]张量理解为 b 张图片,h 行,每行的特征长度为 w*c
-
[b,h * w * c ]张量理解为 b 张图片,每张图片的特征长度为 h_w_c
从语法上来说,视图变换只需要满足新视图的元素总量与内存区域大小相等即可,即新视图的元素数量等于b * h * w *c,而恰恰由于视图的约束很少,完全由用户定义,使得在改变视图时容易出现逻辑隐患
接下来我们继续讨论不合法的视图变换:
例如,如果定义新视图为[b,w,h,c],[b,c,h * w]或者[b,c,h,w]等时,与张量的存储顺序相悖,如果不同步更新张量的存储顺序,那么恢复出的数据将与新视图不一致,从而导致数据错乱。
为了能够正确恢复出数据,必须保证张量的存储顺序与新视图的维度顺序一致
-
根据 图片数量 - 行 - 列 - 通道 初始视图保存的张量,按照 图片数量 - 行 - 列 - 通道(b-h-w-c)的顺序可以获得合法数据。
-
如果按着 图片数量 - 像素 - 通道(b-h * w-c)的恢复视图,也可以获取合法数据
-
如果按着 图片数量 - 通道 - 像素(b-c-h * w)的方式恢复数据,由于内存布局是按着 图片数量 - 行 - 列 - 通道 的顺序,视图维度与存储维度顺序相悖,提取的数据将是错乱的。
改变视图是神经网络中非常常见的操作,可以通过串联多个 Reshape 操作来实现复杂逻辑,但是在通过 Reshape 改变视图时,必须始终记住张量的存储顺序,新视图的维度顺序不能与存储顺序相悖,否则需要通过交换维度操作将存储顺序同步过来。
举个例子:
对于shape 为[4,32,32,3]的图片数据,通过 Reshape 操作将 shape 调整为[4,1024,3],此时视图的维度顺序为b-piexl-c,张量的存储顺序为[b,h,w,c]。
可以将[4,1024,3]恢复为
在 TensorFlow 中,可以通过张量的 ndim 和 shape 成员属性获得张量的维度数和形状:
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
x = tf.range(96)
x = tf.reshape(x, [2, 4, 4, 3])
print(“x.ndim”,x.ndim)
print(“x.shape”,x.shape)
通过 tf.reshape(x, new_shape),可以将张量的视图任意的合法改变:
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
x = tf.range(96)
x = tf.reshape(x, [2, 4, 4, 3])
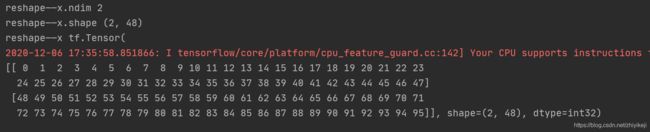
x=tf.reshape(x, [2, -1])
print(“reshape——x.ndim”, x.ndim)
print(“reshape——x.shape”, x.shape)
print(“reshape——x”, x)
下面解释一下相应的参数:
- 参数-1 :表示当前轴上长度需要根据视图总元素不变的法则自动推导,从而方便用户书写。
比如,上面的-1 可以推导为 2 ∗ 4 ∗ 4 ∗ 3 2 \frac{2*4*4*3}{2} 22∗4∗4∗3
再次改变数据的视图为[2,4,12]:
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
x = tf.range(96)
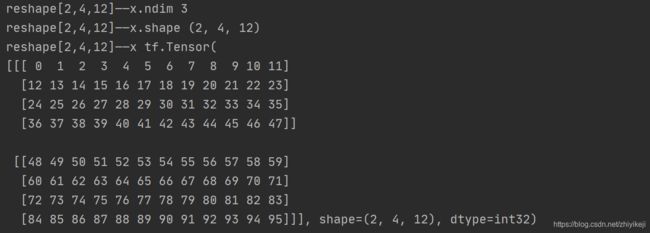
x = tf.reshape(x, [2, 4, 12])
print(“reshape[2,4,12]——x.ndim”, x.ndim)
print(“reshape[2,4,12]——x.shape”, x.shape)
print(“reshape[2,4,12]——x”, x)
下面解释一下[2,4,12]的含义:这是将x的形状变为2行4列,其中每一行有12个元素
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
x = tf.range(96)
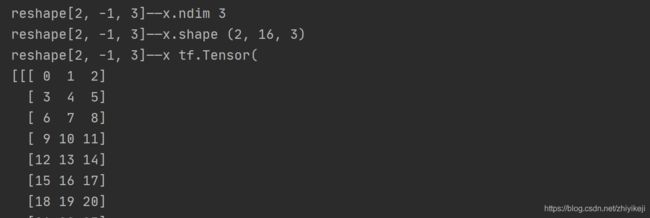
x = tf.reshape(x, [2, -1, 3])
print(“reshape[2, -1, 3]——x.ndim”, x.ndim)
print(“reshape[2, -1, 3]——x.shape”, x.shape)
print(“reshape[2, -1, 3]——x”, x)
下面在解释一下 [2, -1, 3]中-1的含义,它表示: 2 ∗ 4 ∗ 4 ∗ 3 2 ∗ 3 \frac{2*4*4*3}{2*3} 2∗32∗4∗4∗3
经过上面的一系列变换视图,张量的存储顺序始终没有发生任何改变,仍然是在内存中仍然是按着初始写入的顺序0,1,2,…,95保存的。
[](()4.7.2 增删维度
[](()增加维度
增加一个长度为 1 的维度相当于给原有的数据增加一个新维度的概念,维度长度为 1,故数据并不需要改变,仅仅是改变数据的理解方式,因此它其实可以理解为改变视图的一种特殊方式
下面我们考虑一个具体的例子:
一张 28x28 灰度图片的数据保存为 为[28,28]的张量,在末尾给张量增加一新维度,定义为为通道数维度,此时张量的 shape 变为[28,28,1]:
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
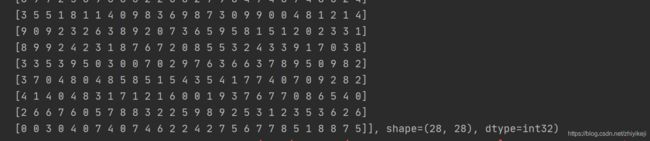
x = tf.random.uniform([28, 28], maxval=10, dtype=tf.int32)
print(x)
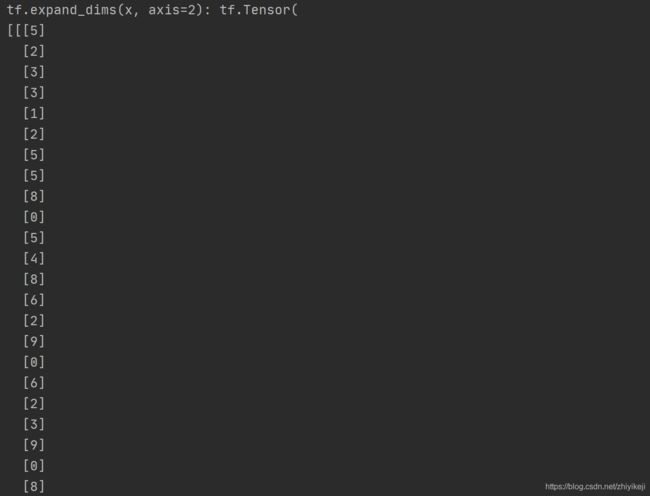
通过 tf.expand_dims(x, axis)可在指定的 axis 轴前可以插入一个新的维度:
x=tf.expand_dims(x, axis=2)
我们先对比一下插入前和插入后的数据:
- 插入前:
- 插入后:
可以看到,插入一个新维度后,数据的存储顺序并没有改变,依然按着5,2,3,3,1…的顺序保存,仅仅是在插入一个新的维度后,改变了数据的视图
同样的方法,我们可以在最前面插入一个新的维度,并命名为图片数量维度,长度为1,此时张量的 shape 变为[1,28,28,1]
注意:tf.expand_dims 的 axis
-
为正时,表示在当前维度之前插入一个新维度
-
为负时,表示当前维度之后插入一个新的维度
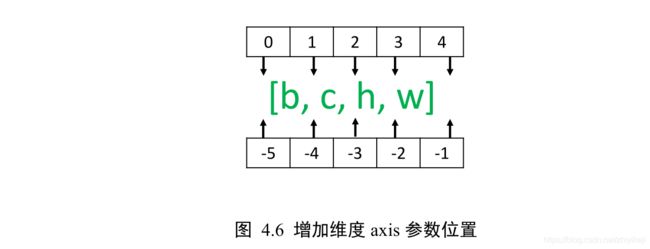
以[,ℎ, ,]张量为例,不同 axis 参数的实际插入位置如下图 4.6 所示:
[](()删除维度
是增加维度的逆操作,与增加维度一样,删除维度只能删除长度为 1 的维
度,也不会改变张量的存储。继续考虑增加维度后 shape 为[1,28,28,1]的例子。
如果希望将图片数量维度删除,可以通过 tf.squeeze(x, axis)函数,axis 参数为待删除的维度的索引号,图片数量的维度轴 axis=0:
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
x = tf.random.uniform([28, 28], maxval=10, dtype=tf.int32)
x = tf.expand_dims(x, axis=2)
x = tf.expand_dims(x, axis=0)
删除维度
x=tf.squeeze(x,axis=0)
print(x)
继续删除通道数维度,由于已经删除了图片数量维度,此时的x的shape 为[28,28,1],因此删除通道数维度时指定 axis=2:
x=tf.squeeze(x,axis=2)
print(“tf.squeeze(x,axis=2)”,x)
但是如果不指定维度参数 axis,即 tf.squeeze(x),那么他会默认删除所有长度为 1 的维度:
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
x = tf.random.uniform([1, 28, 28, 1], maxval=10, dtype=tf.int32)
print(“未删除前:”, x.shape)
x = tf.squeeze(x)
print(“删除后:”,x.shape)
[](()4.7.3 交换维度
改变视图、增删维度都不会影响张量的存储。在实现算法逻辑时,在保持维度顺序不变的条件下,仅仅改变张量的理解方式是不够的,有时需要直接调整的存储顺序,即交换维度(Transpose)。通过交换维度,改变了张量的存储顺序,同时也改变了张量的视图。
交换维度操作是非常常见的,比如在 TensorFlow 中,图片张量的默认存储格式是通道后行格式:[b,h,w,c],但是部分库的图片格式是通道先行:[b,c,h,w],因此需要完成[b,h,w,c]到[b,c,h,w]维度交换运算。
我们以[b,h,w,c]转换到[b,c,h,w]为例,介绍如何使用tf.transpose(x, perm)函数完成维度交换操作,其中
- perm表示新维度顺序List
考虑图片张量 shape 为[2,32,32,3], 图片数量、行、列、通道数 的维度索引分别为 0,1,2,3,如果需要交换为[b,c,h,w]格式,则新维度的排序为 图片数量、通道数、行、列 ,对应的索引号为[0,3,1,2],实现如下:
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
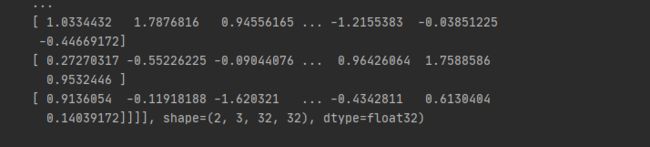
x = tf.random.normal([2, 32, 32, 3])
x=tf.transpose(x, perm=[0, 3, 1, 2])
print(x)
下面大致解释一下上面的代码:
perm后面的顺序就是原始对应位置进行交换后的顺序,也就是说原来3号位对应的位置现在放在2号位置上
如果希望将[b,h,w,c]交换为[b,w,h,c],即将行列维度互换,则新维度索引为[0,2,1,3]:
注意:通过 tf.transpose 完成维度交换后,张量的存储顺序已经改变,视图也随之改变,后续的所有操作必须基于新的存续顺序进行
[](()4.7.4 数据复制
-
当通过增加维度操作插入新维度后,可能希望在新的维度上面复制若干份数据,满足后续算法的格式要求。
-
考虑 = @ + 的例子,偏置插入新维度后,需要在新维度上复制 batch size(步长尺寸) 份数据,将 shape 变为与@一致后,才能完成张量相加运算。
-
可以通过tf.tile(x, multiples)函数完成数据在指定维度上的复制操作
multiples 分别指定了每个维度上面的复制倍数
-
对应位置为 1 表明不复制
-
为 2 表明新长度为原来的长度的 2 倍,即数据复制一份,以此类推。
以输入为[2,4],输出为 3 个节点线性变换层为例,偏置定义为:
通过 tf.expand_dims(b,axis=0)插入新维度:样本数量维度
此时的 shape 变为[1,3],我们需要在 axis=0 图片数量维度上根据输入样本的数量复制若干次,这里的 batch size 为 2,变为矩阵 B:
实现以上结果,我们可以通过以下步骤:
通过 tf.tile(b, multiples=[2,1])即可在 axis=0 维度复制 1 次在 axis=1 维度不复制。
axis=0表示[1,3]中的1也就是一行,上面的代码就是将第一行复制一次
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
b = tf.constant([1, 2])
print(“初始状态下:”, b)
b = tf.expand_dims(b, axis=0)
print(“在0号位插入一个新的维度:”, b)
b=tf.tile(b,multiples=[2,1])
print(“复制一次之后:”,b)
我们在看一个例子
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
x=tf.range(4)
x=tf.reshape(x,[2,2])
print(“未复制之前的x:”,x)
x=tf.tile(x,multiples=[1,2])
print(“在列维度上复制一份数据:”,x)
x=tf.tile(x,multiples=[2,1])
print(“在行维度上复制一份数据:”,x)
需要注意的是,tf.tile 会创建一个新的张量来保存复制后的张量,由于复制操作涉及到大量数据的读写 IO 运算,计算代价相对较高。
神经网络中不同 shape 之间的运算操作十分频繁,那么有没有轻量级的复制操作呢?这就是接下来要介绍的 Broadcasting 操作。
[](()4.8 Broadcasting
Broadcasting 也叫广播机制(自动扩展也许更合适),它是一种轻量级张量复制的手段,在逻辑上扩展张量数据的形状,但是只要在需要时才会执行实际存储复制操作。
对于大部分场景,Broadcasting 机制都能通过优化手段避免实际复制数据而完成逻辑运算,从而相对于 tf.tile 函数,减少了大量计算代价。
对于所有长度为 1 的维度,Broadcasting 的效果和 tf.tile 一样,都能在此维度上逻辑复
制数据若干份,但是区别在于
-
tf.tile 会创建一个新的张量,执行复制 IO 操作,并保存复制后的张量数据
-
Broadcasting 并不会立即复制数据,它会逻辑上改变张量的形状,使得视图上变成了复制后的形状
Broadcasting 会通过深度学习框架的优化手段避免实际复制数据而完成逻辑运算,至于怎么实现的我们不用考虑,对于用户来说,Broadcasting 和 tf.tile 复制的最终效果是一样的,操作对用户透明,但是 Broadcasting 机制节省了大量计算资源,建议在运算过程中尽可能地利用 Broadcasting 提高计算效率。
继续考虑上述的Y = X@W+ 的例子,X@W的 shape 为[2,3],的 shape 为[3],我们可以通过结合 tf.expand_dims 和 tf.tile 完成实际复制数据运算,将变换为[2,3],然后与X@W完成相加。但实际上,我们直接将 shape 为[2,3]与[3]的相加:
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
x = tf.random.normal([2, 4])
w = tf.random.normal([4, 3])
b = tf.random.normal([3])
y = x @ w + b
print(y)
我们可以看出上述加法并没有发生逻辑错误,那么它是怎么实现的呢?
这是因为它自动调用 Broadcasting函数 tf.broadcast_to(x, new_shape),将 2 者 shape 扩张为相同的[2,3],即上式可以等效为:
y = x@w + tf.broadcast_to(b,[2,3])
也就是说,操作符+在遇到 shape 不一致的 2 个张量时,会自动考虑将 2 个张量Broadcasting 到一致的 shape,然后再调用 tf.add 完成张量相加运算
这也就解释了我们之前一直存在的困惑。通过自动调用 tf.broadcast_to(b, [2,3])的 Broadcasting 机制,既实现了
增加维度、复制数据的目的,又避免实际复制数据的昂贵计算代价,同时书写更加简洁高效。
那么有了 Broadcasting 机制后,所有 shape 不一致的张量是不是都可以直接完成运算了呢?
很明显,所有的运算都需要在正确逻辑下进行,Broadcasting 机制并不会扰乱正常的计算逻辑,它只会针对于最常见的场景自动完成增加维度并复制数据的功能,提高开发效率和运行效率。这种最常见的场景是什么呢?
这就要说到 Broadcasting 设计的核心思想。
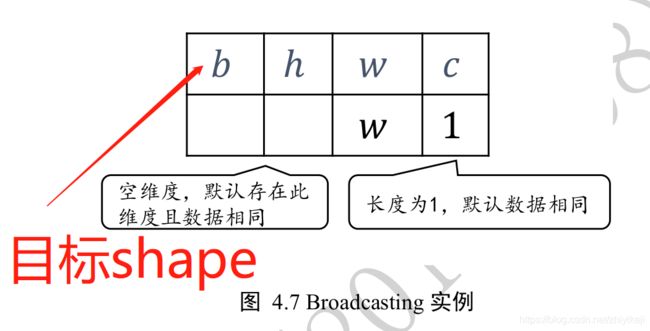
Broadcasting 机制的核心思想是普适性,即同一份数据能普遍适合于其他位置。在验证普适性之前,需要将张量 shape 靠右对齐,然后进行普适性判断:对于长度为 1 的维度,默认这个数据普遍适合于当前维度的其他位置;对于不存在的维度,则在增加新维度后默认当前数据也是普适性于新维度的,从而可以扩展为更多维度数、其他长度的张量形状。
这段话可能读起来比较难理解,下面我们通过一个例子去理解它:
考虑 shape 为[w,1]的张量 A,需要扩展为 shape:[b,h,w,c],如图 4.7 所示,上行为欲扩展的 shape,下面为现有 shape:
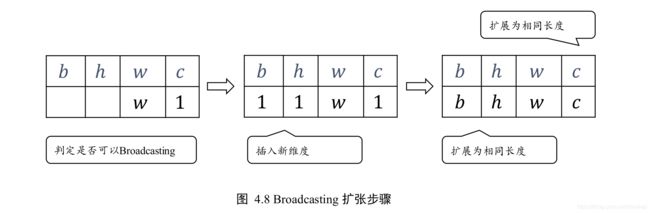
下面我们经过如下几个步骤来实现:
-
将 2 个 shape 靠右对齐
-
对于通道维度 c,张量的现长度为 1,则默认此数据同样适合当前维度的其他位置,将数据逻辑上复制c − 1份,长度变为 c;
-
对于不存在的 b 和 h 维度,则自动插入新维度,新维度长度为 1,同时默认当前的数据普适于新维度的其他位置,即对于其它的图片、其他的行来说,与当前的这一行的数据完全一致。
-
这样将数据b,h 维度的长度自动扩展为 b,h,如图 4.8 所示:
通过 tf.broadcast_to(x, new_shape)可以显式将现有 shape 扩张为 new_shape:
a = tf.random.normal([32, 1])
a = tf.broadcast_to(a, [2, 32, 32, 3])
print(a)
下面我们来考虑不满足普适性原则的例子,如下图 4.9 所示:
在 c 维度上,张量已经有 2 个特征数据,新 shape 对应维度长度为 c(c ≠ 2,比如 c=3),那么当前维度上的这 2 个特征无法普适到其他长度,故不满足普适性原则,无法应用Broadcasting 机制,将会触发错误:
a = tf.random.normal([32, 2])
a=tf.broadcast_to(a, [2, 32, 32, 4])
print(a)
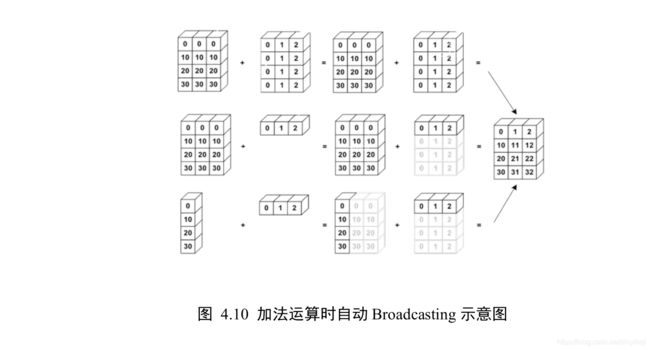
在进行张量运算时,有些运算可以在处理不同 shape 的张量时,会隐式自动调用Broadcasting 机制,如+,-,*,/等运算等,将参与运算的张量 Broadcasting 成一个公共shape,再进行相应的计算,如图 4.10 所示,演示了 3 种不同 shape 下的张量 A,B 相加的例子:
[](()4.9 数学运算
[](()4.9.1 加减乘除
加减乘除是最基本的数学运算,分别通过:
-
tf.add 加
-
tf.subtract 减
-
tf.multiply 乘
-
tf.divide 除
但是TensorFlow 已经重载了+ −∗/运算符,一般推荐直接使用运算符来完成加减乘除运算。
整除和余除也是常见的运算之一,分别通过//和%运算符实现。
我们来演示整除运算:
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
a = tf.range(5)
print(“a”, a)
b = tf.constant(2)
print(“b:”, b)
c = a // b
print(“a//b:”, c)
下面解释一下这个原理:
0//2=0 1//2=0 2//2=1 3//2=1 4//2=2
余除运算
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
d = a % b
print(“a%b”, d)
0%2=0 1%2=1 2%2=0 3%2=1 4%2=0
[](()4.9.2 乘方
通过 tf.pow(x, a)可以方便地完成 y = x a y=x^a y=xa乘方运算,也可以通过运算符**实现x ∗∗ a运算,实现如下:
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
x = tf.range(4)
print(“未运算之前:”,x)
x = tf.pow(x, 3)
print(“运算之后:”,x)
设置指数为 1 a \frac{1}{a} a1 形式即可实现根号运算 x a \sqrt[a]{x} ax
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
x = tf.constant([1., 4., 9.])
print(“未运算之前:”, x)
x = x ** (0.5)
print(“运算之后:”, x)
对于常见的平方和平方根运算,可以使用
-
tf.square(x) 实现平方操作
-
tf.sqrt(x) 实现开根号操作
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
x = tf.range(5)
x = tf.cast(x, dtype=tf.float32)
print(“未运算之前:”, x)
x = tf.square(x)
print(“运算之后:”, x)
x=tf.sqrt(x)
print(“开平方之后:”, x)
[](()4.9.3 指数 对数
通过 tf.pow(a, x)或者**运算符可以方便实现指数运算 a x a^x ax
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
x=tf.constant([1,2,3])
y=tf.pow(2,x)
print(y)
- 对于自然指数 e x e^x ex可以通过 tf.exp(x)实现:
print(tf.exp(1.))
![]()
- 在 TensorFlow 中,自然对数 log e x \log_e^{x} logex可以通过 tf.math.log(x)实现:
x = tf.exp(3.)
x = tf.math.log(x)
print(x)
- 对其他底数的对数进行计算:
我们可以通过换底公式:
间接的通过 tf.math.log(x)实现。
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
x = tf.constant([1., 2.])
x = 10 ** x
print(“x:”, x)
y = tf.math.log(x) / tf.math.log(10.)
print(“y”, y)
[](()4.9.4 矩阵相乘
神经网络中间包含了大量的矩阵相乘运算,前面我们已经介绍了通过@运算符可以方便的实现矩阵相乘,还可以通过
tf.matmul(a, b)实现。需要注意的是,TensorFlow 中的矩阵相乘可以使用批量方式,也就是张量 a,b 的维度数可以大于 2。当张量 a,b 维度数大于2时,TensorFlow 会选择 a,b 的最后两个维度进行矩阵相乘,前面所有的维度都视作 Batch 维度
根据矩阵相乘的定义,a 和 b 能够矩阵相乘的条件是,a 的倒数第一个维度长度(列)和b 的倒数第二个维度长度(行)必须相等。
比如:张量 a shape:[4,3,28,32]可以与张量 b shape:[4,3,32,2]进行矩阵相乘:
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
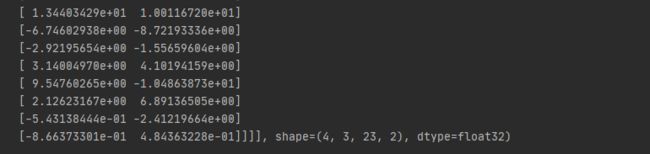
a = tf.random.normal([4, 3, 23, 32])
b = tf.random.normal([4, 3, 32, 2])
print(a @ b)
矩阵相乘函数支持自动 Broadcasting 机制:
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
a=tf.random.normal([4,28,32])
b=tf.random.normal([32,16])
print(tf.matmul(a,b))
[](()4.10 前向传播实战
本节我们将利用我们已经学到的知识去完成三层神经网络的实现:
我们采用的数据集是 MNIST 手写数字图片集,输入节点数为 784,第一层的输出节点数是256,第二层的输出节点数是 128,第三层的输出节点是 10,也就是当前样本属于 10 类别的概率。
- 首先创建每个非线性函数的 w,b 参数张量:
w1 = tf.Variable(tf.random.truncated_normal([784, 256], stddev=0.1))
b1 = tf.Variable(tf.zeros([256]))
w2 = tf.Variable(tf.random.truncated_normal([256, 128], stddev=0.1))
b2 = tf.Variable(tf.zeros([128]))
w3 = tf.Variable(tf.random.truncated_normal([128, 10], stddev=0.1))
b3 = tf.Variable(tf.zeros([10]))
- 在前向计算时,首先将 shape 为[b,28,28]的输入数据 Reshape 为[b,784] 即 [b, 28, 28] => [b, 28*28]
x=tf.range(784)
x = tf.reshape(x, [-1, 28*28])
- 完成第一个非线性函数的计算,我们这里显示地进行 Broadcasting:大致过程如下:
度数大于2时,TensorFlow 会选择 a,b 的最后两个维度进行矩阵相乘,前面所有的维度都视作 Batch 维度
根据矩阵相乘的定义,a 和 b 能够矩阵相乘的条件是,a 的倒数第一个维度长度(列)和b 的倒数第二个维度长度(行)必须相等。
比如:张量 a shape:[4,3,28,32]可以与张量 b shape:[4,3,32,2]进行矩阵相乘:
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
a = tf.random.normal([4, 3, 23, 32])
b = tf.random.normal([4, 3, 32, 2])
print(a @ b)
矩阵相乘函数支持自动 Broadcasting 机制:
import tensorflow as tf
from tensorflow_core.python import keras
from tensorflow.keras import layers
import numpy as np
a=tf.random.normal([4,28,32])
b=tf.random.normal([32,16])
print(tf.matmul(a,b))
[](()4.10 前向传播实战
本节我们将利用我们已经学到的知识去完成三层神经网络的实现:
我们采用的数据集是 MNIST 手写数字图片集,输入节点数为 784,第一层的输出节点数是256,第二层的输出节点数是 128,第三层的输出节点是 10,也就是当前样本属于 10 类别的概率。
- 首先创建每个非线性函数的 w,b 参数张量:
w1 = tf.Variable(tf.random.truncated_normal([784, 256], stddev=0.1))
b1 = tf.Variable(tf.zeros([256]))
w2 = tf.Variable(tf.random.truncated_normal([256, 128], stddev=0.1))
b2 = tf.Variable(tf.zeros([128]))
w3 = tf.Variable(tf.random.truncated_normal([128, 10], stddev=0.1))
b3 = tf.Variable(tf.zeros([10]))
- 在前向计算时,首先将 shape 为[b,28,28]的输入数据 Reshape 为[b,784] 即 [b, 28, 28] => [b, 28*28]
x=tf.range(784)
x = tf.reshape(x, [-1, 28*28])
- 完成第一个非线性函数的计算,我们这里显示地进行 Broadcasting:大致过程如下: