直方图均衡化原理及计算

直方图均衡化是基于灰度直方图的图像增强的一种方法，还有另外一种方法是直方图规定化。

均衡化的目的是将原始图像的直方图变为均衡分布的的形式，将一非均匀灰度概率密度分布图像，通过寻求某种灰度变换，变成一幅具有均匀概率密度分布的目的图像。

具体原理如下：

1、连续灰度级：

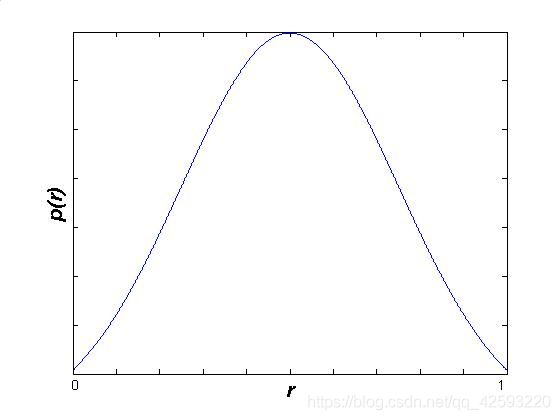
假定：r代表灰度级，P(r)为概率密度函数。r值已经过归一化处理，灰度值范围在[0,1]之间。r与P(r)之间的关系如下：

                                                                             非均匀分布的连续灰度直方图

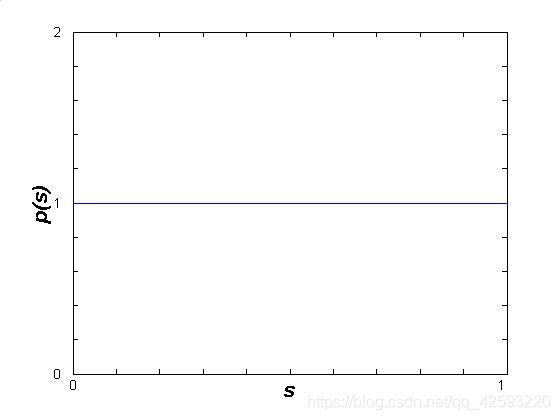
均衡化的目的是将上面的非均匀分布变成如下图所示的均匀分布：

                                                                              均匀分布的连续灰度直方图

我们接下来要做的是要找到一种变换S=T(r)使直方图变平直，为使变换后的灰度仍保持从黑到白的单一变化顺序，且变换范围与原先一致，以避免整体变亮或变暗，需要有如下规定：

（1）在0 <= r <= 1中，T(r)是单调递增函数，且0 <= T(r) <= 1；

（2）反变换r=(s)，(s)也为单调递增函数，且0 <= s <= 1。

                                                                           直方图均衡化变换公式推导图示

 

 因为灰度变换不影响像素的位置分布，而且也不会增减像素数目，所以有如下的推导公式：

 

 2、离散灰度级：

设一幅图像的像素总数为n，分为L个灰度级，其中：

：表示第K个灰度级出现的个数。

：第K个灰度级出现的概率。

（0<=<=1, k=0,1,2,...,L-1），公式如下：

计算的基本步骤如下：

（1）求出图像中所包含的灰度级,一般都经过归一化处理，范围在[0,1]之间，也可以定在[0,L-1]之间。

（2）统计各灰度级的像素数目（k=0,1,2,...,L-1）。

（3）计算图像直方图。

（4）计算变换函数，即：

（5）用变换函数计算映射后输出的灰度级。

（6）统计映射后新的灰度级的像素数目。

（7）计算输出图像的直方图。

根据上面推导出来的公式以及计算步骤，我们可以结合栗子来加深理解~~~

 

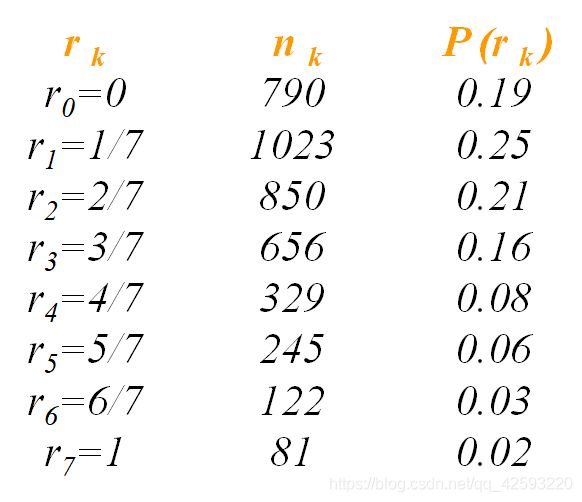
eg：设图像有64*64=4096的像素，有8个灰度级，灰度分布如下所示：

由上图我们知道该图像的，和，下一步我们要做的就是通过变换函数求，即：

...

依次可求得，，，，。

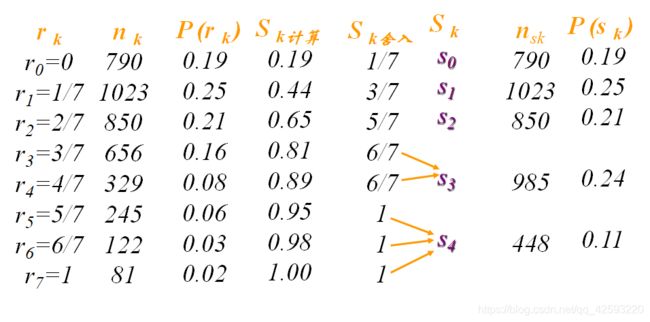
由于原图像的灰度级只有8级，变换之后的只能选择最接近的一个灰度级，因此需要对进行舍入处理，即上述步骤中的第五步，对每个将以1/7为量化单位进行舍入运算，结果如下：

，，，，，，，

根据舍入后的结果，我们可以得到均衡化后的灰度级仅有5个级别，分别是：

，，，，

接下来我们就可以统计映射后新的灰度级的像素数目，然后就可得到均衡化后的概率密度函数。
结合图来看可能更直观一点：

均衡化后的直方图比较：

应用到实际图像中：

 

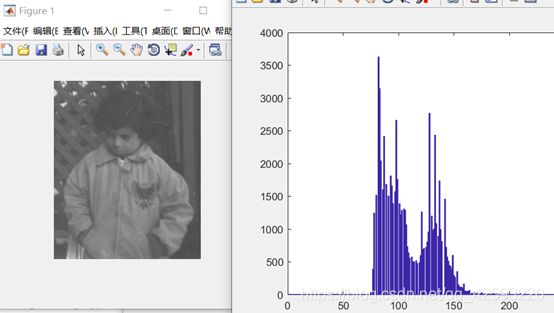
均衡化前的图像和直方图：

均衡化后的图像和直方图：

 

最后总结：

直方图均衡化实质上是减少图像的灰度级来加大对比度，图像经均衡化处理之后，图像变得清晰，直方图中每个像素点的灰度级减少，但分布更加均匀，对比度更高。

但直方图均衡化技术仍存在如下缺点：

（1）将原始函数的累积分布函数作为变换函数，只能产生近似均匀的直方图。

（2）在某些情况下，并不一定需要具有均匀直方图的图像。