HashMap为啥初始化大小是16
HashMap的默认初始化长度是多少?
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16
在JDK1.8的 235 行有1<<4就是16,为啥用位运算呢?直接写16不好么?这里主要是位运算的性能好,为啥位运算性能就好,那是因为位运算人家直接操作内存,不需要进行进制转换,要知道计算机可是以二进制的形式做数据存储啊,知道了吧,那16嘞?为啥是16不是其他的?想要知道为啥是16,我们得从HashMap的数据存放特性来说。
对于HashMap而言,存放的是键值对,所以做数据添加操作的时候会根据你传入的key值做hash运算,从而得到一个下标值,也就是以这个下标值来确定你的这个value值应该存放在底层Node数组的哪个位置。
那么这里一定会出现的问题就是,不同的key会被计算得出同一个位置,那么这样就冲突啦,位置已经被占了,那么怎么办嘞?
首先就是冲突了,我们要想办法看看后来的数据应该放在哪里,就是给它找个新位置,这是常规方法,除此之外,我们是不是也可以聚焦到hash算法这块,就是尽量减少冲突,让得到的下标值能够均匀分布。
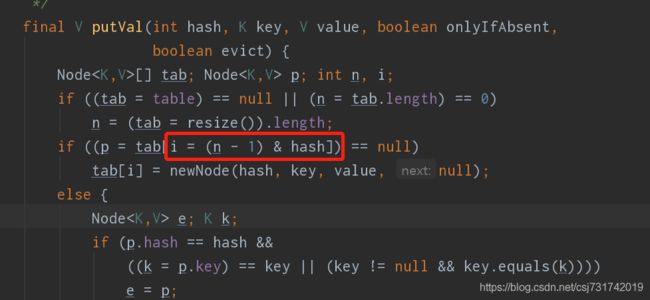
这是在源码中第629行有这么一段,它就是计算我们上面说的下标值的,这里的n就是数组长度,默认的就是16,这个hash就是这里得到的值:(i = (n - 1) & hash)
关于上面的hash值怎么来,如下所示:
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
举个例子:
下面我们以值为“book”的Key来演示整个过程:
1.计算book的hashcode(ps: "book".hashCode() ),结果为十进制的3029737,二进制的101110001110101110 1001。
2.假定HashMap长度是默认的16,计算Length-1的结果为十进制的15,二进制的1111。
3.把以上两个结果做与运算,101110001110101110 1001 & 1111 = 1001,十进制是9,所以 index=9。
可以说,Hash算法最终得到的index结果,完全取决于Key的Hashcode值的最后几位。
继续看它:
i = (n - 1) & hash
这里是做位与运算,接着我们还需要先搞明白一个问题
为什么要进行取模运算以及位运算?
要知道,我们最终是根据key通过哈希算法得到下标值,这个是怎么得到的呢?通常做法就是拿到key的hashcode然后与数组的容量做取模运算,为啥要做取模运算呢?
比如这里默认是一个长度为16的Node数组,我们现在要根据传进来的key计算一个下标值出来然后把value放入到正确的位置,想一下,我们用key的hashcode与数组长度做取模运算,得到的下标值是不是一定在数组的长度范围之内,也就是得到的下标值不会出现越界的情况。
要知道取模是怎么回事啊!明白了这点,我们再来看:
i = (n - 1) & hash
这里就是计算下标的,为啥不是取模运算而是位与运算呢?使用位与运算的一方面原因就是它的性能比较好,另外一点就是这里有这么一个等式:
(n - 1) & hash = hash % n
因此,总结起来就是使用位与运算可以实现和取模运算相同的效果,而且位与运算性能更高!
接着,我们再看一个问题
为什么要减一做位运算?
理解了这个问题,我们就快接近为什么容量是2的整数次幂的答案了,根据上面说的,这里的n-1是为了实现与取模运算相同的效果,除此之外还有很重要的原因在里面。
在此之前,我们需要看看什么是位与运算,因为我怕这块知识大家之前不注意忘掉了,而它对理解我们现在所讲的问题很重要,看例子:
比如拿5和3做位与运算,也就是5 & 3 = 1(操作的是二进制),怎么来的呢?
5转换为二进制:0000 0000 0000 0000 0000 0000 0000 0101
3转换为二进制:0000 0000 0000 0000 0000 0000 0000 0011
1转换为二进制:0000 0000 0000 0000 0000 0000 0000 0001
所以啊,位与运算的操作就是:第一个操作数的的第n位于第二个操作数的第n位如果都是1,那么结果的第n位也为1,否则为0
看懂了吧,不懂得话可以去补补这块的知识,后续我也会单独发文详细说说这块。
我们继续回到之前的问题,为什么做减一操作以及容量为啥是2的整数次幂,为啥嘞?
告诉你个秘密,2的整数次幂减一得到的数非常特殊,有啥特殊嘞,就是2的整数次幂得到的结果的二进制,如果某位上是1的话,那么2的整数次幂减一的结果的二进制,之前为1的后面全是1
啥意思嘞,可能有点绕,我们先看2的整数次幂啊,有2,4,8,16,32等等,我们来看,首先是16的二进制是:10000,接着16减一得15,15的二进制是:1111,再形象一点就是:
16转换为二进制:0000 0000 0000 0000 0000 0000 0001 0000
15转换为二进制:0000 0000 0000 0000 0000 0000 0000 1111
再对照我给你说的秘密,看看懂了不,可以再来个例子:
32转换为二进制:0000 0000 0000 0000 0000 0000 0010 0000
31转换为二进制:0000 0000 0000 0000 0000 0000 0001 1111
这会总该懂了吧,然后我们再看计算下标的公式:
(n - 1) & hash = n % hash
n是容量,它是2的整数次幂,然后与得到的hash值做位于运算,因为n是2的整数次幂,减一之后的二进制最后几位都是1,再根据位与运算的特性,与hash位与之后,得到的结果是不是可能是0也可能是1,,也就是说最终的结果取决于hash的值,如此一来,只要输入的hashcode值本身是均匀分布的,那么hash算法得到的结果就是均匀的。
啥意思?这样得到的下标值就是均匀分布的啊,那冲突的几率就减少啦。
而如果容量不是2的整数次幂的话,就没有上述说的那个特性,这样冲突的概率就会增大。
举个例子:
假设HashMap的长度是10,运算步骤
是的,虽然HashCode的倒数第二第三位从0变成了1,但是运算的结果都是1001。也就是说,当HashMap长度为10的时候,有些index结果的出现几率会更大,而有些index结果永远不会出现(比如0111)!这样,显然不符合Hash算法均匀分布的原则。反观长度16或者其他2的幂,Length-1的值是所有二进制位全为1,这种情况下,index的结果等同于HashCode后几位的值。只要输入的HashCode本身分布均匀,Hash算法的结果就是均匀的。
所以,明白了为啥容量是2的整数次幂了吧。
那为啥是16嘞?难道不是2的整数次幂都行嘛?理论上是都行,但是如果是2,4或者8会不会有点小,添加不了多少数据就会扩容,也就是会频繁扩容,这样岂不是影响性能,那为啥不是32或者更大,那不就浪费空间了嘛,所以啊,16就作为一个非常合适的经验值保留了下来