哈希表的构造之线性探测法
哈希表在我们实际生活中运用的还是相当广泛的,比如:海量数据处理的时候,当然是要在哈希上进行变通拓展的。要想能运用它就得了解它,下来我们就先从哈希表的基础说起。
1.哈希表的定义
哈希表(Hash table,也叫散列表),是依据关键码值(Key)而直接进行访问在内存存储位置的数据结构。也就是说,它通过一个关键值的函数将所需的数据映射到表中的位置来访问数据,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
2.构造哈希表经常使用的散列函数的方法有:
(1)直接定址法---取关键字的某个线性函数为散列地址,Hash(Key)= Key或Hash(Key)= A*Key + B,A、B为常数。但是这种方法有很大的缺陷,就是当关键码比较分散时,hash表的所浪费的空间是非常大的。
(2)除留余数法---取关键值被某个不大于散列表长m的数p除后的所得的余数为散列地址。Hash(Key)= Key% P。
(3)平方取中法---取key平方后的中间几位作为散列地址。
(4)折叠法------将关键字分割成位数相同的几部分,最后一部分位数可以不同,然后取这几部分的叠加和(去除进位)作为散列地址。数位叠加可以有移位叠加和间界叠加两种方法。移位叠加是将分割后的每一部分的最低位对齐,然后相加;间界叠加是从一端向另一端沿分割界来回折叠,然后对齐相加。
(5)随机数法-----选择一个随机函数,取关键字的随机值作为散列地址,通常用于关键字长度不同的场合。
(6)数学分析法---分析一组数据,比方一组员工的出生年月日,这时我们发现出生年月日的前几位数字大体同样,这种话,出现冲突的几率就会非常大,可是我们发现年月日的后几位表示月份和详细日期的数字区别非常大,假设用后面的数字来构成散列地址,则冲突的几率会明显减少。因此数字分析法就是找出数字的规律,尽可能利用这些数据来构造冲突几率较低的散列地址。
但是这里还存在一个问题(任意的散列函数都不能避免):
通常关键码的集合比散列表地址集合大的多,因此经过散列函数计算后,把不同的关键码映射到同一散列地址上,这就产生了冲突。冲突太多还会降低搜索的效率,所以我们一般对于给定的关键码集合要选择一个计算简单且地址分布均匀的散列函数。
3.哈希冲突
3.1 首先先明确造成哈希冲突的几种原因:
(1)散列函数,一个好的散列函数的值应尽可能平均分布(这里选择的是除留余数法);
(2)处理冲突方法;
(3)负载因子的大小。太小不一定就好,并且浪费空间严重,负载因子和散列函数是联动的。
3.3 负载因子(也称载荷因子)的概念
4.还需注意以下几个问题
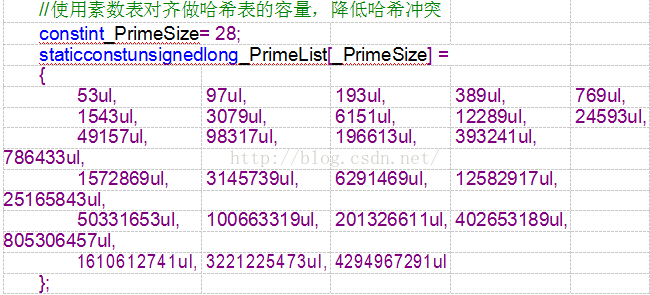
4.1素数表(使用素数做除数可以减少哈希冲突),也就是如何对哈希表进行扩容。
4.2 字符串哈希该如何解决
//字符串哈希算法(将字符串转为整型)
template<>
struct _HashFunc //模板的特化
{
static size_t BKDRHash(const char* str) //BKDRHash算法
{
unsigned int seed= 131;// 31 131 1313 13131 131313
unsigned int hash= 0;
while(*str)
{
hash=hash*seed+(*str++);
}
return(hash& 0x7FFFFFFF);
}
size_t operator()(const string& str)
{
return BKDRHash(str.c_str());
}
};
5.查找
今天先实现用线性探测的方法解决哈希冲突:
enum Status
{
EXIST,
DELETE,
EMPTY
};
template
struct HashTableNode
{
K _key;
V _value;
Status _status;
HashTableNode(const K& key=K(),const V& value=V())
:_key(key)
,_value(value)
,_status(EMPTY)
{}
};
template //仿函数
struct _HashFunc
{
size_t operator()(const K& key)
{
return key;
}
};
//字符串哈希算法(将字符串转为整型)
template<>
struct _HashFunc //模板的特化
{
static size_t BKDRHash(const char* str) //BKDRHash算法
{
unsigned int seed= 131;// 31 131 1313 13131 131313
unsigned int hash= 0;
while(*str)
{
hash=hash*seed+(*str++);
}
return(hash& 0x7FFFFFFF);
}
size_t operator()(const string& str)
{
return BKDRHash(str.c_str());
}
};
template>
class HashTable
{
typedef HashTableNode Node;
public:
HashTable()
:_size(0)
{
_tables.resize(_GetNextPrime(0));
}
HashTable(const HashTable& ht)
{
size_t NewSize=ht._tables.size();
_tables.resize(NewSize);
for(size_t i=0;i<_tables.size();++i)
{
if(_tables[i]==EXIST)
{
_tables[i]._key=ht._tables[i]._key;
_tables[i]._value=ht._tables[i]._value;
_tables[i]._status=EXIST;
}
}
_size=ht._size;
}
HashTable& operator=(HashTable& ht)
{
if(this != &ht)
{
HashTable h(ht);
ht._Swap(h);
}
return *this;
}
bool Insert(const K& key,const V& value)
{
_CheckSize();
size_t index=_HashFunc(key);
while(_tables[index]._status==EXIST) //找不为空的位置进行插入
{
if(_tables[index]._key==key) //已经存在的值不再插入
return false;
++index;
if(index==_tables.size())
index=0;
}
_tables[index]._key=key;
_tables[index]._value=value;
_tables[index]._status=EXIST;
++_size;
return true;
}
Node* Find(const K& key)
{
size_t index=_HashFunc(key);
size_t src=index;
while(_tables[index]._status!=EMPTY) //有些可能是删除的,要跳过继续查询
{
if(_tables[index]._key == key && _tables[index]._status!=DELETE)
return &_tables[index];
else
{
++index;
if(index==_tables.size())
{
index=0;
}
if(index==src)
break; //找了一圈还没找到就跳出去
}
}
return NULL;
}
bool Remove(const K& key)
{
Node* ret=Find(key);
if(NULL==ret)
return false;
//懒删除法
else
{
ret->_status=DELETE;
--_size;
return true;
}
}
protected:
size_t _HashFunc(const K& key)
{
//HashFunc hf;
//return hf(key)%_tables.size();
return HashFunc()(key)%_tables.size(); //匿名对象调仿函数
}
size_t _GetNextPrime(size_t num)
{
const int _PrimeSize= 28;
static const unsigned long _PrimeList[_PrimeSize] =
{
53ul, 97ul, 193ul, 389ul, 769ul,
1543ul, 3079ul, 6151ul, 12289ul, 24593ul,
49157ul, 98317ul, 196613ul, 393241ul,
786433ul,
1572869ul, 3145739ul, 6291469ul, 12582917ul,
25165843ul,
50331653ul, 100663319ul, 201326611ul, 402653189ul,
805306457ul,
1610612741ul, 3221225473ul, 4294967291ul
};
for(size_t i=0;i<_PrimeSize;++i)
{
if(num < _PrimeList[i])
{
return _PrimeList[i];
}
return _PrimeList[i-1];
}
return _PrimeList[_PrimeSize-1]; //如果size大于或等于素数表中数据,就返回表中最大数
}
//当哈希表size=0或超过负载因子的要求时就该扩容
void _CheckSize()
{
if(_tables.size()==0 || _size*10 / _tables.size()>=8)
{
size_t NewSize=_GetNextPrime(_tables.size());
HashTable h;
h._tables.resize(NewSize);
for(size_t i=0;i<_tables.size();++i)
{
if(_tables[i]._status==EXIST)
h.Insert(_tables[i]._key,_tables[i]._value);
}
this->_Swap(h); //通过临时对象出作用域自动析构的特性
}
}
void _Swap(HashTable& h)
{
_tables.swap(h._tables);
swap(_size,h._size);
}
protected:
vector _tables;
size_t _size;
};