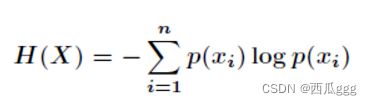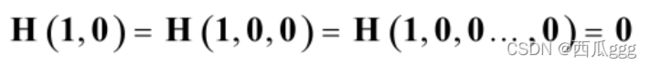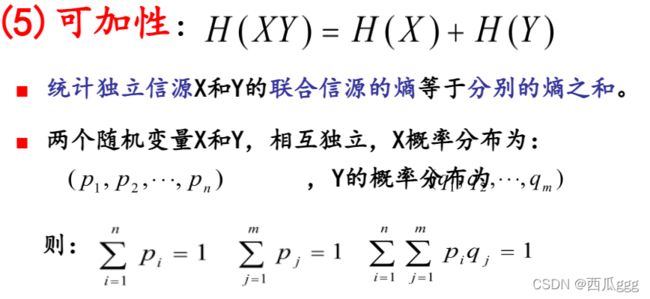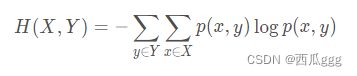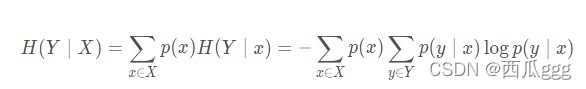熵及相关名称含义

最近在用互信息的一些知识，有些

1.熵（entropy）

系统混乱程度的度量，系统越混乱，熵越大。当完全均匀分布时，这个系统的熵就达到了最大值，也就是说此时的系统越混乱。

对于事件来说，当所有状态概率相等的时候熵最大，这个时候系统对取什么态没有偏向性，所以混乱度最大。

在信息世界，熵越高，则能传输越多的信息，熵越低，则意味着传输的信息越少。（这里指的是信息量）

2.信息熵（information entropy）

信息量的大小的度量，用于描述随机变量的不确定度。事件的不确定性越大，则信息量越大，信息熵越大。

2.1定义

 

2.2性质

（1）对称性：当p(xi)任意变换时，熵函数的值不变

 

（2）确定性：

 

（3）非负性

 

（4）扩展性

 

（5）可加性质

 

（6）强可加性

 

（7）极值性

 

（8）条件减少熵

当人们拥有关于另外一个随机系统的知识的时候，对于人们所关注的随机系统来说，它剩下的不确定性一定不会增加，至少是保持不变，一般情况下不确定性会减少

3.互信息（Mutual Information）

互信息是两个随机变量间相互依赖性的量度，互信息度量两个随机变量共享的信息——知道随机变量X,对随机变量Y的不确定性减少的程度（或者知道随机变量Y，对随机变量X的不确定性减少的程度，用I(X;Y)表示

3.1定义

对于两个随机变量 和 ，如果其联合分布为 ,边缘分布为 ,则互信息可以定义为：

 

为了理解互信息的涵义，我们把公式中的对数项分解

 

        我们知道概率取负对数表征了当前概率发生所代表的信息量。上式表明，两事件的互信息为各自事件单独发生所代表的信息量之和减去两事件同时发生所代表的信息量之后剩余的信息量，这表明了两事件单独发生给出的信息量之和是有重复的，互信息度量了这种重复的信息量大小。最后再求概率和表示了两事件互信息量的期望。从式中也可以看出，当两事件完全独立时，p ( x , y ) = p ( x ) ⋅ p ( y ) p(x,y)=p(x)\cdot p(y)p(x,y)=p(x)⋅p(y)，互信息计算为 0 00，这也是与常识判断相吻合的。（本小节转自信息熵及其相关概念_Northan的博客-CSDN博客_信息熵）

4.联合熵 (Joint Entropy)

两个离散随机变量 X XX 和 Y YY 的联合熵为：

 

联合熵表征了两事件同时发生系统的不确定度。

5条件熵（Conditional Entropy）

条件熵H(Y∣X) 表示在已知随机变量 X的条件下随机变量 Y 的不确定性。

 

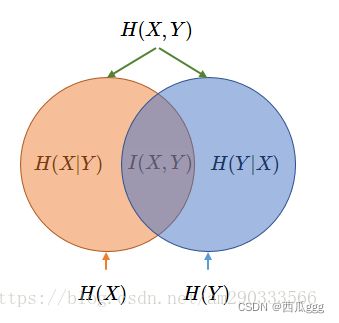
6.互信息、联合熵、条件熵之间的关系

 

I(X,Y)=H(X)+H(Y)−H(X,Y)=H(Y)−H(Y∣X)=H(X)−H(X∣Y)=H(X,Y)−H(Y∣X)−H(X∣Y)

7.相对熵（relative entropy,或称 Kullback-Leiblerdivergence, KL 距离)）

相对熵又称KL散度，用于衡量对于同一个随机变量x的两个分布p(x)和q(x)之间的差异。在机器学习中，p(x)常用于描述样本的真实分布，例如[1,0,0,0]表示样本属于第一类，而q(x)则常常用于表示预测的分布，例如[0.7,0.1,0.1,0.1]。显然使用q(x)来描述样本不如p(x)准确，q(x)需要不断地学习来拟合准确的分布p(x)。

KL散度的公式如下：

 

KL散度的值越小表示两个分布越接近

 

8交叉熵（cross entropy）

我们将KL散度的公式进行变形，得到：

 

前半部分就是p(x)的熵，后半部分就是我们的交叉熵：

 

机器学习中，我们常常使用KL散度来评估predict和label之间的差别，但是由于KL散度的前半部分是一个常量，所以我们常常将后半部分的交叉熵作为损失函数，其实二者是一样的。