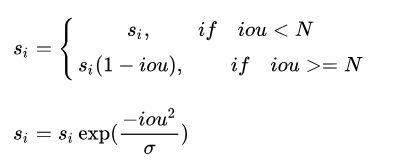【深度学习】Tricks

图像方面的tricks

分类

以精度提升为目的

（1）增加额外数据

（2）更加细化已有分类

让每一类的特征更加明显，例如都是车，但可以细分为：越野车，城市越野车，跑车，卡车，拖挂车等；

（3）数据增强

该方法是为了扩大数据的多样性。常规包括以下几种方式：

• 旋转，上下翻转，左右翻转，镜像，仿射变换，颜色通道变换，亮度变换，色相变换，饱和度变换，随机裁剪，高斯、中值、平均模糊，对比度增强，锐化，以及将前面的几种变换组合成为一种变换。这里需要提醒的是并不是使用的增强方法越多效果越好，每一种数据都有其有效性，我认为一般情况下选用其中的4-6个变换即可，这些变换最好能贴合实际情况。另外我发现直接将数据进行增强完训练其效果不如在训练时对数据进行随机的一种或几种变换或不进行变换。https://blog.csdn.net/u013066730/article/details/112252982
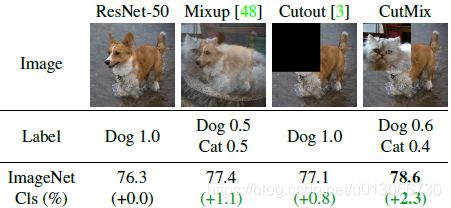
• mixup：将随机的两张样本按比例混合，分类的结果按比例分配https://blog.csdn.net/u013066730/article/details/94716966
• cutmix：就是将一部分区域cut掉但不填充0像素而是随机填充训练集中的其他数据的区域像素值，分类结果按一定的比例分配（如果物体不能放缩，该种方法不适用）https://blog.csdn.net/u013066730/article/details/106354846
• cutout：随机的将样本中的部分区域cut掉，并且填充0像素值，分类的结果不变

• 图像生成：BEGAN的生成；
• 颜色迁移：cyclegan https://blog.csdn.net/u013066730/article/details/100013111，细胞学和组织学的颜色迁移https://github.com/Peter554/StainTools/blob/master/samples/sample.py（仅支持ubuntu）；
• 直接图像复制粘贴，也就是让某一类的数据数量变多，增加他在训练时出现的概率；
• AutoAugment，https://github.com/DeepVoltaire/AutoAugment
• RandAug，https://blog.csdn.net/u013066730/article/details/112367213

（4）增加测试的分辨率

Fixing the train-test resolution discrepancy，，具体的训练方式请参考https://blog.csdn.net/u013066730/article/details/112369794（比赛时专用）

（5）修改损失

• labelsmooth
• focalloss

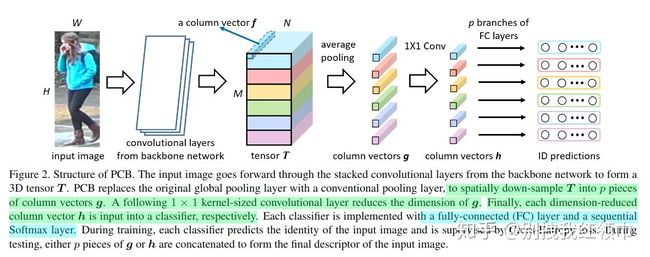
 （6）PCB(Part-based Convolutional Baseline)

在做一些分类问题或者检索问题上可能会有提升，具体参考论文[13]

分割

检测

（1）softNMS

针对的问题是当图片中两个相同类别的物体离得比较近的时候，一般的NMS可能会出现错误抑制的情况，这是因为NMS直接将与最大score的box的IoU有大于某个阈值的其他同类别的box的score直接置为0导致的，这就有点hard了。所以soft NMS就是说不直接将这些满足条件的box直接设置为0而是降低score值，这样循环操作。

有两种形式，线性加权和高斯加权

（2）OHEM (Online Hard Examples Mining)

对于大量正样本负样本比较少的时候，如何挑选对model来说更具有信息性的负样本显得尤为重要。对于batch=M的训练数据，我们从中挑选出loss比较大的样本反向传播。在Faster RCNN中计算RoIs的时候，我们对每个RoI的loss从大到小排序，选择前N个RoIs样本反向传播。

（这里会有一个问题，即位置相近的ROI在map中可能对应的是同一个位置，loss值是相近的，所以如果直接按照loss对roi进行排序的话，选出来的很可能是靠的很近的一些rois，所以针对这个问题，提出的解决方法是：对hard做nms，然后再选择B/N个ROI反向传播，这里nms选择的IoU=0.7。）

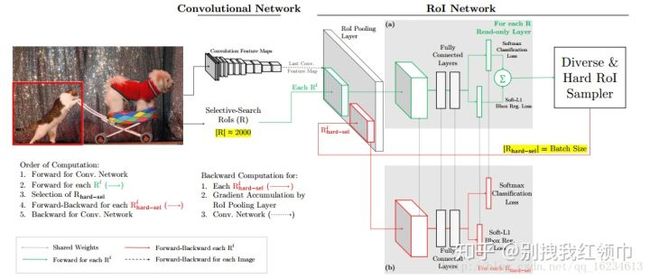
OHEM流程图[4]

[4]中指出是有两种方法，一种是将选出的部分样本再输入红色网络（进行forward和backward）学习并进行梯度传播。而另一种方法是在反向传播时，只对选出的样本的梯度/残差回传，而其他的props的梯度/残差设为0。但这样做容易导致显存显著增加，迭代时间增加。

（3）Deformable Convolution

传统的卷积操作无法适应复杂的几何形变，因为卷积操作的的几何结构是固定的，是一种规则格点的采样方式，而可形变卷积就是在普通卷积上加一个偏移量。类似的还有Deformable ROI Pooling等。

可形变卷积的流程如下：

（1）在原始图像(b,h,w,c)上经过一个普通卷积得到(b,h,w,2c)的输出，这里的2c代表的是x,y两个方向上的偏移量。

（2）将原始图像上的像素索引值与偏移量相加，得到偏移之后的像素索引(限定在图像内部),此时的position是一个float型的坐标值。

（3）使用双线性插值将float坐标值映射得到像素值，在新得到的图像上应用一个普通的卷积。

(b,h,w,c) - > (b,h,w,2c) - > position(b*c,h,w, 2)+ origin image(b*c,h,w)

-> (b*c,h,w) -> (b,h,w,c)

（4）Multi-scale Training/Testing 多尺度训练/测试

训练时，预先定义几个固定的尺度，每个epoch随机选择一个尺度进行训练。测试时，生成几个不同尺度的feature map，对每个Region Proposal，在不同的feature map上也有不同的尺度，我们选择最接近某一固定尺寸（即检测头部的输入尺寸）的Region Proposal作为后续的输入。选择单一尺度的方式被Maxout（element-wise max，逐元素取最大【cascade rcnn中就是】）取代：随机选两个相邻尺度，经过Pooling后使用Maxout进行合并。[5]

（5）一种利用Global Context 全局语境的方法

这一技巧在ResNet的工作中提出，做法是把整张图片作为一个RoI，对其进行RoI Pooling并将得到的feature vector拼接于每个RoI的feature vector上，作为一种辅助信息传入之后的R-CNN子网络。目前，也有把相邻尺度上的RoI【cascede rcnn 中的fpn】互相作为context共同传入的做法。

(6)Box Refinement/Voting 预测框微调/投票法

不同的训练策略，不同的 epoch 预测的结果，使用 NMS 来融合，或者softnms

需要调整的参数： box voting 的阈值。不同的输入中这个框至少出现了几次来允许它输出，得分的阈值，一个目标框的得分低于这个阈值的时候，就删掉这个目标框。

Box Voting[9]想法是根据NMS被抑制掉重合度较高的box进一步refine NMS之后的边框。主要做法步骤是：

（7）mixup数据增强

1. 对于输入的一个batch的待测图片images，我们将其和随机抽取的图片进行融合，融合比例为lam，得到混合张量inputs；
2. 第1步中图片融合的比例lam是[0,1]之间的随机实数，符合beta分布，相加时两张图对应的每个像素值直接相加，即 inputs = lam*images + (1-lam)*images_random；
3. 将1中得到的混合张量inputs传递给model得到输出张量outpus，随后计算损失函数时，我们针对两个图片的标签分别计算损失函数，然后按照比例lam进行损失函数的加权求和，即loss = lam * criterion(outputs, targets_a) + (1 - lam) * criterion(outputs, targets_b)；

目标检测中的实现可以参考gluoncv[7]中的实现。

mix_image 就是两张图片直接相加。

img1, label1 = self._dataset[idx]
lambd = 1

# draw a random lambda ratio from distribution
if self._mixup is not None:
    lambd = max(0, min(1, self._mixup(*self._mixup_args)))

if lambd >= 1:
    weights1 = np.ones((label1.shape[0], 1))
    label1 = np.hstack((label1, weights1))
    return img1, label1

# second image
idx2 = np.random.choice(np.delete(np.arange(len(self)), idx))
img2, label2 = self._dataset[idx2]

# mixup two images
height = max(img1.shape[0], img2.shape[0])
width = max(img1.shape[1], img2.shape[1])
mix_img = mx.nd.zeros(shape=(height, width, 3), dtype='float32')
mix_img[:img1.shape[0], :img1.shape[1], :] = img1.astype('float32') * lambd
mix_img[:img2.shape[0], :img2.shape[1], :] += img2.astype('float32') * (1. - lambd)
mix_img = mix_img.astype('uint8')
y1 = np.hstack((label1, np.full((label1.shape[0], 1), lambd)))
y2 = np.hstack((label2, np.full((label2.shape[0], 1), 1. - lambd)))
mix_label = np.vstack((y1, y2))
return mix_img, mix_label

（8）Cacade-RCNN

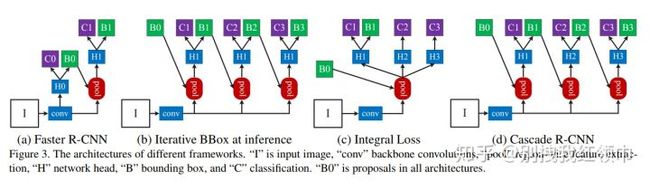
cascade-rcnn主要针对的问题是：训练阶段和测试阶段，bounding box回归器的输入分布是不一样的。training阶段的输入proposals质量更高(被采样过，IoU>threshold)，inference阶段的输入proposals质量相对较差（没有被采样过，因为不知道gt），这就是论文中提到mismatch问题，这个问题是固有存在的，通常threshold取0.5时，mismatch问题还不会很严重。

而为了提高bounding box回归器输入的proposals的质量而一味的提高IoU的阈值会导致过拟合问题和更严重的mismatch问题。因此作者提出了cascade-rcnn结构。

如上图所示，和Iterative BBox比较，Iterative BBox的H位置都是共享的，而且3个分支的IoU阈值都取0.5。而Integral Loss共用pooling，只有一个stage，但有3个不共享的H，每个H处都对应不同的IoU阈值。

Cascade R-CNN使用cascade回归作为一种重采样的机制，逐stage提高proposal的IoU值，从而使得前一个stage重新采样过的proposals能够适应下一个有更高阈值的stage。

• 每一个stage的detector都不会过拟合，都有足够满足阈值条件的样本。
• 更深层的detector也就可以优化更大阈值的proposals。
• 每个stage的H不相同，意味着可以适应多级的分布。
• 在inference时，虽然最开始RPN提出的proposals质量依然不高，但在每经过一个stage后质量都会提高，从而和有更高IoU阈值的detector之间不会有很严重的mismatch。

（9）Group Normalization

可以从三个点来看GN比BN“好用”的原因[11]：

• BN需要区分train和evaluate过程，而GN不用
• BN对batch size敏感，而GN与batch size独立（包括loss与accuracy等），BN的性能会随着训练的batch size变小而急剧下降（让BN在某些受内存限制而需要输入小batch的任务上效果不好）
• 小batch size的时候，GN效果要比BN好（原因就是第二点）

而GN在速度上，通常比BN要慢，这是因为GN相对于BN来说，有额外的transpose与reshape操作，当层数加深的时候，训练速度也按比例下降。

福音是pytorch days ago已经可以通过简单的接口实现GN了

def get_gn(num_channels):
    return nn.GroupNorm(32, num_channels)  # Separate num_channels into 32 groups

model = models.ResNet(models.Bottleneck, [3, 4, 6, 3], norm_layer=get_gn)

（10）FPN(Feature Pyramid Network)

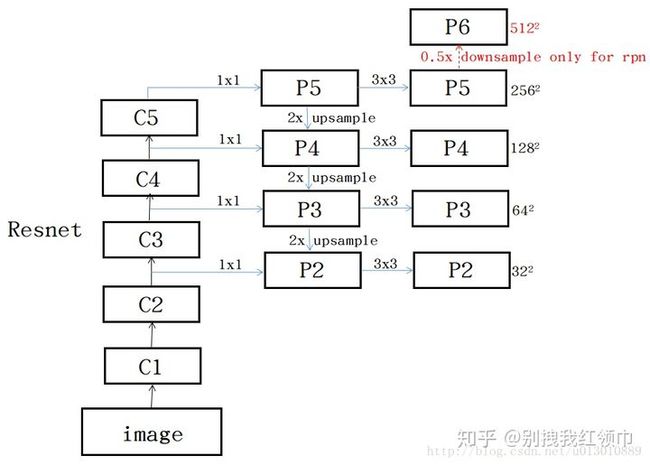
主要是针对待检测物体尺度的问题做的改进，如图[12]所示，每个level的feature P2，P3，P4，P5，P6只对应一种scale，比例还是3个比例。分别在这些level的feature上进行roi的计算。

（11）数据预处理和数据增强

针对X光图像像素值普遍偏高，大都在200以上，所以除了减均值归一化之外，看到有的同学会做像素值的映射变换操作，目的是为了降低像素值，从而让像素值可以基本上均匀的散布在[0, 255]之间，用的映射函数类似于一个二次函数。

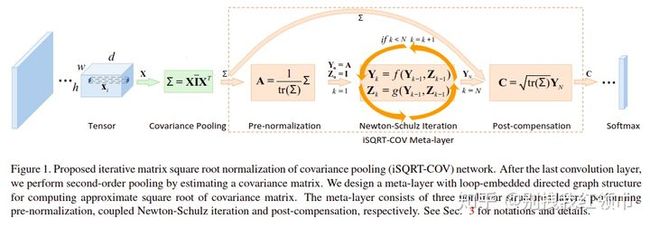
（12）ISQRT Conv Net(iterative matrix square root normalization of covariance pooling (iSQRT-COV),)

协方差池化的迭代矩阵平方根标准化[14]、[15]

文中提出了用一个二阶甚至高阶的统计方法来替换一阶的全局平均池化，即将一阶的均值替换为二阶的协方差，幂值取经验值0.5，其优点在于能够利用深度网络学习后的各通道之间的相关信息。之前求协方差平方根的方法是将协方差进行本征分解得到本征值，然后求本征值的平方根。但是基于 GPU 的平台对本征分解的支持都非常差，所以本文在求协方差的平方根时，不再使用本征分解，而是使用迭代法，称为 iSQRT-COV。而这种迭代法非常适合大规模的 GPU 实现，提高了计算效率。

中间的meta-layer包含三个层，分别进行预正则化，牛顿-舒尔茨迭代和后补偿处理。第一层(pre-normalization)将协方差矩阵除以它的迹以保证下一个阶段的牛顿-舒尔茨迭代的可收敛性；第二层则是一个循环结构，进行一定次数的耦合矩阵方程迭代以计算合适的矩阵平方根；第三层乘以协方差矩阵迹的平方根来抵消第一层改变数据的量级的影响。meta-layer的输出是一个对称矩阵，然后将这个矩阵的上三角区concate成一个d(d+1)/2 维的向量，再接到后面的ConvNet中进行处理。

（13）weight box fusion(WBF)

文章地址https://arxiv.org/abs/1910.13302， 对应的github代码https://github.com/ZFTurbo/Weighted-Boxes-Fusion

实例分割

NLP方面的tricks

参考

https://zhuanlan.zhihu.com/p/141254917

https://zhuanlan.zhihu.com/p/50621694