近端梯度下降

近端梯度下降

1. 问题模型

目标函数：$minf(x)=g(x)+h(x)$
目标函数$f(x)$为非光滑可导的目标函数，可以将其分为两部分，$g(x)$为凸的光滑可导的函数$h(x)$为凸的非光滑可导的函数。通过解这两个子问题，得到$f(x)$的最优解。

2.基本概念

2.1 投影算子

投影算子$pro{x}_f:R^n\to R^n$ 定义为：

可以直观地理解为，希望找到一个$x$既要最小化$f(x)$，又希望$x$尽可能地与$v$点接近
如果加入缩放因子$\lambda$，投影算子的定义为：
$$f(x)=1/2x^{T}Ax+b^{T}x+c$$

1. $f(x)=1/2x^{T}Ax+b^{T}x+c$
   $$pro{x}_{\lambda }f(v)=argmi{n}_x(1/2x^{T}Ax+b^{T}x+c+1/2\lambda |(|x-v|){|}_2^2)$$
   当$f(x)+1/2\lambda |(|x-v|){|}_2^2$的梯度为0时，得到$f$在$v$点的投影：
   $$x=(I+\lambda A{)}^{-1}(v-\lambda b)$$
2. $f(x)=|x|$
   $$pro{x}_{\lambda }f(v)=argmi{n}_x(|x|+1/2\lambda |(|x-v|){|}_2^2)$$
   利用软阈值算子：
   
3. $f(x)=I_C(x)$
   .
   $I_C(x)$为集合C上的指示函数，如果$x\in C，I_C(x)=0$，如果$x\notin C，I_C(x)=+\infty$

2.2 Lipschitz连续

如果$\nabla f$是Lipschitz连续的，那么满足
$$||\nabla f(x)-\nabla f(y)|{|}_2\le L||x-y|{|}_2，\forall x,y$$
对一维情况来说,有
$$|\nabla f(x)-\nabla f(y)|\le L|x-y|$$
则, $|\nabla f(x)-\nabla f(y)|/|x-y|\le L$
取极限$limy\to x$得, $|{\nabla }^{2}f(x)|\le L$
根据Taylor展开式得到
$$f(x)\le f(u)+|\nabla f(u){|}^T(x-u)+L/2||x-u|{|}_2^2$$
左式在u附近的极值点可近似为右式在u附近的极值点

3. 近端梯度下降

目标：$minf(x)=g(x)+h(x)$
迭代更新公式：$x^{(k)}=pro{x}_{t_{k}h}(x^{(k-1)}-t_k\nabla g(x^{(k-1)}))$
（$t_k>0$ 为步长，为常数或利用线性搜索法确定）

3.1 算法推导

若有$t\le 1/L$，若$\nabla g(x)$是满足lipschitz连续的，有
$$\begin{array}{rl}f(x)& =h(x)+g(x)\\ & \le h(x)+g(x^k)+\nabla g(x^k{)}^T(x-x^k)+L/2||x-x^k|{|}_2^2\\ & \le h(x)+g(x^k)+\nabla g(x^k{)}^T(x-x^k)+1/2t||x-x^k|{|}_2^2\end{array}$$
$x^{k+1}=argmi{n}_x(h(x)+g(x^k)+\nabla g(x^k{)}^T(x-x^k)+1/2t||x-x^k|{|}_2^2)$
$f(x)$在$x^k$附近的极值点$x^{k+1}$可近似为左端这个目标函数在$x^k$附近的极值点
$$\begin{array}{rl}{x}^{k+1}& =argmi{n}_x(h(x)+g(x^k)+\nabla g(x^k{)}^T(x-x^k)+1/2t||x-x^k|{|}_2^2)\\ & =argmi{n}_x(h(x)+t/2||\nabla g(x^k)|{|}_2^2+\nabla g(x^k{)}^T(x-x^k)+1/2t||x-x^k|{|}_2^2）\\ & =argmi{n}_x(h(x)+1/2t||x-x^k+t\nabla g(x^k)|{|}_2^2)\\ & =pro{x}_{th}(x^k-t\nabla g(x^k))\end{array}$$
$x^{k+1}$ 可近似为$h(x)$在$x^k-t\nabla g(x^k)$处的投影

3.2 具体算法

由于lipschitz常量$L$通常未知，我们无法确定一个小于等于$1/L$的固定步长$t$，因此我们利用线性搜索确定步长，迭代过程可以表示为
given $x^k$,$t^{k-1}$,parameter $\beta \in (0,1)$
let $t:=t^{(}k-1)$
Repeat
    $z:=pro{x}_{\lambda }h(x^k-t\nabla g(x^k))$
    break if $g(z)\le g(x^k)+\nabla g(x^k{)}^T(z-x^k)+1/2t||z-x^k|{|}_2^2$
    update $t:=\beta t$
Return $t^k:=t,x^{k+1}:=z$

$g(z)\le g(x^k)+\nabla g(x^k{)}^T(z-x^k)+1/2t||z-x^k|{|}_2^2$保证的是推导过程中这一步成立（个人理解）

3.3 例子1

$$h(x)=I_C(x)$$
$$pro{x}_{\lambda }h(x^k-t\nabla g(x^k))=argmi{n}_{x\in C}||x-(x^k-t\nabla g(x^k))|{|}_2^2$$

首先根据$g(x)$的负梯度方向找到使$g(x)$最小的迭代点$x_g^k$，然后找$h(x)$在$x_g^k$的投影，由于$h(x)$为集合$C$上的指示函数，其投影算子可以表示为这个函数，表明新的迭代点不能走出集合$C$这个区域，当$g(x)$上的在$x^k$附近的极值点$x^{k+1}$超出集合$C$时，它将会重新投影到集合$C$上。

3.4 加速的近端梯度算法

加入中间变量$y^k$，不是直接对$x^k$求近邻，而是对$y^k$求近邻
given $x^k,t^{k-1}$,parameter $\beta \in (0,1)$
let $t:=t^{(}k-1)$
Repeat
    $w^k=k/(k+3)$
    $y^k:=x^k+w^{k-1}(x^k-x^{k-1})$
    $z:=pro{x}_{\lambda h}(y^k-t\nabla g(y^k))$
    break if $g(z)\le g(y^k)+\nabla g(y^k{)}^T(z-y^k)+1/2t||z-y^k|{|}_2^2$
    update $t:=\beta t$
Return $t^k:=t,x^{(}k+1):=z$

3.5 例子2——LASSO回归问题

$$minf(x)=1/2||Ax-b|{|}_2^2+p||x|{|}_1$$
$$\begin{gathered} x_g^k=x^{k-1}-t\nabla g(x^{k-1})=x^{k-1}-t{A}^T(A{x}^{k-1}-b) \\ {x}^k=pro{x}_{t_{k}h}(x_g^k)=argmi{n}_x(p||x|{|}_1+1/2t||x-x_g^k|{|}_2^2) \end{gathered}$$
求解第二个方程时用到了软阈值，

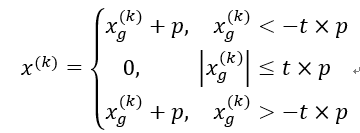
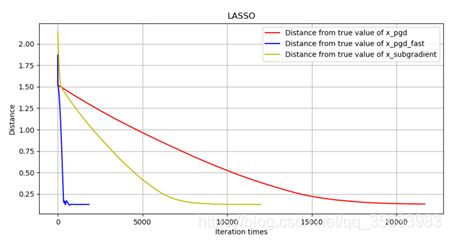
实验结果：
加速的近端梯度下降算法比近端梯度下降算法的速度快了很多，同时，我们同次梯度算法的效果进行了对比，发现快速近端梯度下降算法的收敛速度优势十分明显。

4. 结论

对于凸函数$h(x)$，其近端投影$pro{x}_{ht}$有解析解； $pro{x}_{ht}$仅仅依赖于$h$，因此可以被用于不同的$g$函数；$g$可以使任意复杂的函数，只要我们能计算其梯度；很多目标函数虽然是凸的，但是可能不可导，通过寻找投影可以解的其最优解，比次梯度法可能具有更好的收敛特性。