词嵌入方法:GloVe模型
前言
词向量的表示方法主要有两种代表算法,基于不同的思想:
- 一种是基于全局矩阵分解的方法,如LSA
- 一种是局部上下文窗口的方法,如Mikolov在2013年提出来的CBOW和skip-gram方法
但是这两种方法都有各自的缺陷,其中,LSA虽然有效利用了统计信息,但是在词汇类比方面却很差,而CBOW和skip-gram虽然可以很好地进行词汇类比,但是因为这两种方法是基于一个个局部的上下文窗口方法,因此,没有有效地利用全局的词汇共现统计信息。
为了克服全局矩阵分解和局部上下文窗口的缺陷,在2014年,Jeffrey Pennington等人提出了一种新的GloVe方法,该方法基于全局词汇共现的统计信息来学习词向量,从而将统计信息与局部上下文窗口方法的优点都结合起来,并发现其效果确实得到了提升。
GloVe原理
1.模型概述
目标:进行词的向量化表示,使得向量之间尽可能多地蕴含语义和语法的信息
输入:语料库(文本)
输出:词向量
方法概述:基于语料库构建词的共现矩阵,然后基于共现矩阵和GloVe模型学习词向量
2.共现矩阵统计
设共现矩阵为 X X X,其元素为 X i , j X_{i,j} Xi,j,意义为:在整个语料库中,单词 i i i和单词 j j j共同出现在一个窗口中的次数。
设置语料库输入:i love you but you love him i am sad
这个小小的语料库只有1个句子,涉及到7个单词:i、love、you、but、him、am、sad。
如果我们采用一个窗口宽度为5(左右长度都为2)的统计窗口,那么就有以下窗口内容:
| 窗口标号 | 中心词 | 窗口内容 |
|---|---|---|
| 0 | i | i love you |
| 1 | love | i love you but |
| 2 | you | i love you but you |
| 3 | but | love you but you love |
| 4 | you | you but you love him |
| 5 | love | but you love him i |
| 6 | him | you love him i am |
| 7 | i | love him i am sad |
| 8 | am | him i am sad |
| 9 | sad | i am sad |
窗口0、1长度小于5是因为中心词左侧内容少于2个,同理窗口8、9长度也小于5。
以窗口5为例说明如何构造共现矩阵:
中心词为love,语境词为but、you、him、i;则执行:
- X l o v e , b u t + = 1 X_{love,but}+=1 Xlove,but+=1
- X l o v e , y o u + = 1 X_{love,you}+=1 Xlove,you+=1
- X l o v e , h i m + = 1 X_{love,him}+=1 Xlove,him+=1
- X l o v e , i + = 1 X_{love,i}+=1 Xlove,i+=1
使用窗口将整个语料库遍历一遍,即可得到共现矩阵X。
3.GloVe模型训练词向量
3.1模型公式
损失函数:

v i v_i vi, v j v_j vj是单词 i i i和单词 j j j的词向量 b i b_i bi, b j b_j bj是两个标量(作者定义的偏差项), f f f是权重函数(具体函数公式及功能下一节介绍), N N N是词汇表的大小(共现矩阵维度为N*N)。可以看到,GloVe模型没有使用神经网络的方法
3.2模型推导
3.2.1模型初步
符号变量:

统计某一单词对于其他单词同时一共出现的次数,也就是出现在 i i i上下文的单词综述

统计某一个单词 i i i和另一单词 k k k出现的次数占 i i i单词一共出现次数的比例,也就是 k k k出现在 i i i的上下文的概率

条件概率,表示单词 k k k与单词 i i i, j j j的相关性,统计结果如下表所示
| r a t i o i , j , k ratio_{i,j,k} ratioi,j,k | j , k j,k j,k相关 | j , k j,k j,k不相关 |
|---|---|---|
| i , k i,k i,k相关 | 趋近1 | 很大 |
| i , k i,k i,k不相关 | 很小 | 趋近1 |
思想:假设我们已经得到了词向量,如果我们用词向量 v i , v j , v k v_i,v_j,v_k vi,vj,vk 通过某种函数计算 r a t i o i , j , k ratio_{i,j,k} ratioi,j,k能够同样得到这样的规律的话,就意味着我们词向量与共现矩阵具有很好的一致性,也就说明我们的词向量中蕴含了共现矩阵中所蕴含的信息。
设用词向量 v i , v j , v k v_i,v_j,v_k vi,vj,vk 计算 r a t i o i , j , k ratio_{i,j,k} ratioi,j,k的函数为 g ( v i , v j , v k ) g(v_i,v_j,v_k) g(vi,vj,vk),应该有:
 即二者应该尽可能地接近;
即二者应该尽可能地接近;
很容易想到用二者的差方来作为代价函数:
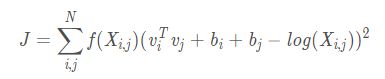
3.2.2模型简化
但是仔细一看,模型中包含3个单词,这就意味着要在 N 3 N^3 N3的复杂度上进行计算,太复杂了,最好能再简单点。
作者的想法:
- 要考虑单词 i i i和单词 j j j之间的关系,那 g ( v i , v j , v k ) g(v_i,v_j,v_k) g(vi,vj,vk)中大概要有这么一项吧: v i − v j vi−vj vi−vj嗯,合理,在线性空间中考察两个向量的相似性,不失线性地考察,那么 v i − v j vi−vj vi−vj大概是个合理的选择;
- r a t i o i , j , k ratio_{i,j,k} ratioi,j,k,是个标量,那么 g ( v i , v j , v k ) g(v_i,v_j,v_k) g(vi,vj,vk),最后应该是个标量啊,虽然其输入都是向量,那內积应该是合理的选择,于是应该有这么一项 ( v i − v j ) T v k (v_i-v_j)^Tv_k (vi−vj)Tvk
- 然后作者又往 ( v i − v j ) T v k (v_i-v_j)^Tv_k (vi−vj)Tvk的外面套了一层指数运算exp(),得到最终的 g ( v i , v j , v k ) = e x p ( ( v i − v j ) T v k ) g(v_i,v_j,v_k)=exp((v_i-v_j)^Tv_k) g(vi,vj,vk)=exp((vi−vj)Tvk)

然后就发现找到简化方法了:只需要让上式分子对应相等,分母对应相等,即: P i , k = e x p ( v i T v k ) P_{i,k}=exp(v_i^Tv_k) Pi,k=exp(viTvk)和 P j , k = e x p ( v j T v k ) P_{j,k}=exp(v_j^Tv_k) Pj,k=exp(vjTvk)然而分子分母形式相同,就可以把两者统一考虑了,即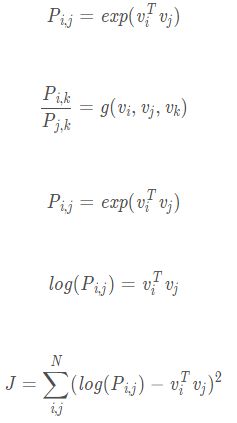
现在只需要在 N 2 N^2 N2的复杂度上进行计算,而不是 N 3 N^3 N3,现在关于为什么第3步中,外面套一层exp()就清楚了,正是因为套了一层exp(),才使得差形式变成商形式,进而等式两边分子分母对应相等,进而简化模型。
然而,出了点问题。
仔细看这两个式子:
l o g ( P i , j ) = v i T v j log(P_{i,j})=v_i^Tv_j log(Pi,j)=viTvj和 l o g ( P j , i ) = v j T v i log(P_{j,i})=v_j^Tv_i log(Pj,i)=vjTvi等式左侧不具有对称性,但是右侧具有对称性。
将代价函数中的条件概率展开
4.总结
Cbow/Skip-Gram 是一个local context window的方法,比如使用NS来训练,缺乏了整体的词和词的关系,负样本采用sample的方式会缺失词的关系信息。
另外,直接训练Skip-Gram类型的算法,很容易使得高曝光词汇得到过多的权重
Global Vector融合了矩阵分解Latent Semantic Analysis (LSA)的全局统计信息和local context window优势。融入全局的先验统计信息,可以加快模型的训练速度,又可以控制词的相对权重。
skip-gram、CBOW每次都是用一个窗口中的信息更新出词向量,但是Glove则是用了全局的信息(共线矩阵),也就是多个窗口进行更新
参考
1.https://blog.csdn.net/linchuhai/article/details/97135612?utm_medium=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase
2.https://blog.csdn.net/u014665013/article/details/79642083?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase
3.https://blog.csdn.net/coderTC/article/details/73864097