小白学习点云处理的基础知识和相关概念理解

体素(voxel)：

是体积元素(volumepixel)的简称。一如其名，是数字数据于三维空间分割上的最小单位，体素用于三维成像、科学数据与医学影像等领域。概念上类似二维空间的最小单位——像素，像素用在二维计算机图像的影像数据上。有些真正的三维显示器运用体素来描述它们的分辨率，举例来说：可以显示512×512×512体素的显示器。如同像素，体素本身并不含有空间中位置的数据(即它们的坐标)，然而却可以从它们相对于其它体素的位置来推敲，意即它们在构成单一张体积影像的数据结构中的位置。（图中第三个）

面元：

在计算数学中，用很多小的平面描述一个曲面。这些小的平面就叫“面元”。可理解为曲面上的小单元。面元矢量在某个方向上，若有多于一个面元构成一个平面，则在该方向上就存在一个矢量（有方向的直线）。（图中第二个）

CNN：

是一个前馈式神经网络，能从一个二维图像中提取其拓扑结构，采用反向传播算法来优化网络结构，求解网络中的未知参数。CNN是一类特别设计用来处理二维数据的多层神经网络。CNN被认为是第一个真正成功的采用多层层次结构网络的具有鲁棒性的深度学习方法。CNN通过挖掘数据中的空间上的相关性，来减少网络中的可训练参数的数量，达到改进前向传播网络的反向传播算法效率，因为CNN需要非常少的数据预处理工作，所以也被认为是一种深度学习的方法。在CNN中，图像中的小块区域（也叫做“局部感知区域”）被当做层次结构中的底层的输入数据，信息通过前向传播经过网络中的各个层，在每一层中都由过滤器构成，以便能够获得观测数据的一些显著特征。因为局部感知区域能够获得一些基础的特征，比如图像中的边界和角落等，这种方法能够提供一定程度对位移、拉伸和旋转的相对不变性。它的非全连接和权值共享的网络结构使之更类似于生物神经网络，降低了网络模型的复杂度（对于很难学习的深层结构来说，这是非常重要的），减少了权值的数量。

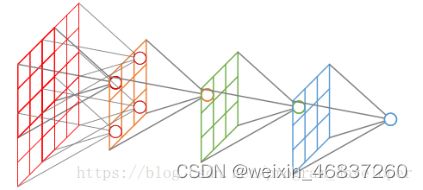
感受野：

在卷积神经网络中，感受野（Receptive Field）的定义是卷积神经网络每一层输出的特征图（feature map）上的像素点在输入图片上映射的区域大小。再通俗点的解释是，特征图上的一个点对应输入图上的区域，如图所示。

 

PCL中分割_欧式分割：

基于欧式距离的分割和基于区域生长的分割本质上都是用区分邻里关系远近来完成的。由于点云数据提供了更高维度的数据，故有很多信息可以提取获得。

欧几里得算法使用邻居之间距离作为判定标准，而区域生长算法则利用了法线，曲率，颜色等信息来判断点云是否应该聚成一类。                

从前有一个脑筋急转弯，说一个锅里有两粒豆子，如果不用手，要怎么把它们分开。当时的答案是豆子本来就是分开的，又没黏在一起，怎么不叫分开。OK，实际上 欧几里德算法就是这个意思。两团点云就像是两粒豆子，只要找到某个合适的度量方式，就有办法把点云和点云分开。区分豆子我们用的方法可以归结为，两个豆子之间的距离小于分子距离，所以它们并没有连在一起。如果两团点云之间最近两点的距离小于单个点云内部点之间的距离，则可以由算法判断其分为两类。假设总点云集合为A，聚类所得点云团为Q，具体的实现方法大致是：

1. 找到空间中某点p10，用kdTree找到离他最近的n个点，判断这n个点到p的距离。将距离小于阈值r的点p12、p13、p14…放在类Q里；
2. 在 Q\p10 里找到一点p12，重复1；
3. 在 Q\p10、p12 找到找到一点，重复1，找到p22、p23、p24…全部放进Q里；
4. 当 Q 再也不能有新点加入了，则完成搜索了。

听起来好像这个算法并没什么用，因为点云总是连成片的，很少有什么东西会浮在空中让你来分。但是如果和前面介绍的内容联系起来就会发现这个算法威力巨大了。比如：
半径滤波删除离群点
采样一致找到桌面
抽掉桌面…

当然，一旦桌面被剔除，桌上的物体就自然成了一个个的浮空点云团。就能够直接用欧几里德算法进行分割了，这样就可以提取出我们想要识别的东西。在这里我们就可以使用提取平面，利用聚类的方法，平面去掉再显示剩下的所有聚类的结果，虽然都把平面和各种非平面提取出来了，但是怎么把非平面的聚类对象可视化出来呢？提取出来的聚类的对象都是单独的显示在相对与源文件不变的位置所以我们直接相加就应该可以实现。

区域生长算法原理：

区域生长算法直观感觉上和欧几里德算法相差不大，都是从一个点出发，最终占领整个被分割区域。古话说：“星星之火，可以燎原” 就是这个意思。欧几里德算法是通过距离远近，来判断烧到哪儿。区域生长算法则不然，烧到哪儿靠燃料（点）的性质是否类似来决定。对于普通点云，其可由法线、曲率估计算法获得其法线和曲率值。通过法线和曲率来判断某点是否属于该类。

算法的主要思想是：首先依据点的曲率值对点进行排序。之所以排序是因为，区域生长算法是从曲率最小的点开始生长的，这个点就是初始种子点，初始种子点所在的区域即为最平滑的区域，从最平滑的区域开始生长可减少分割片段的总数，提高效率。设置一个空的种子点序列和空的聚类区域，选好初始种子后，将其加入到种子点序列中，并搜索邻域点，对每一个邻域点，比较邻域点的法线与当前种子点的法线之间的夹角，小于平滑阈值的将当前点加入到当前区域，然后检测每一个邻域点的曲率值，小于曲率阈值的加入到种子点序列中，删除当前的种子点，循环执行以上步骤，直到种子序列为空。

其算法可以总结为：

选择曲率最小的点为初始种子点，将种子周围的点和种子相比；

1. 法线之间的夹角小于阈值，法线方向足够相近；
2. 曲率足够小；

如果满足1、2，则该点可用做种子点，并删除当前的种子点；

如果只满足1，则归类到当前区域而不做种子点；

从某个种子出发，其“子种子”不再出现，则一类聚集完成；

类的规模既不能太大也不能太小。

显然，上述算法是针对小曲率变化面设计的。尤其适合对连续阶梯平面进行分割。

kdTree ：

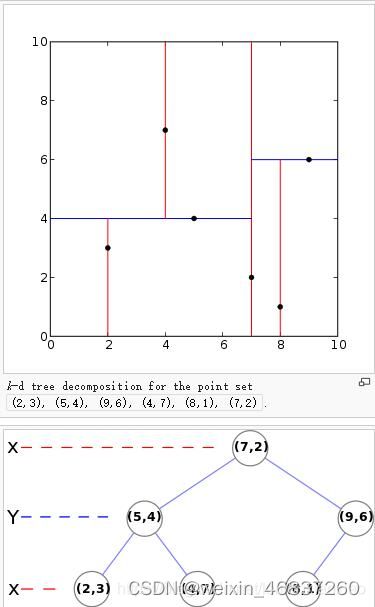
建立 kdTree 实际上是一个不断划分的过程，首先选择最sparse的维度，然后找到该维度上的中间点，垂直该维度做第一次划分。此时k维超平面被一分为二，在两个子平面中再找最sparse的维度，依次类推知道最后一个点也被划分。那么就形了一个不断二分的树。如图所示：

 

显然，一般情况下一个点的邻近点只需要在其父节点和子节点中搜索即可，大大缩小了邻近点的搜索规模。并且 kdtree 可以有效的对插入点进行判断其最近点在哪个位置。对于低层次视觉来说 kdTree 算法是非常重要的。在很多情况下需要给出某个点，再查k临近点的编号，或者差某半径范围内的点。

OcTree：

OcTree 是一种更容易理解也更自然的思想。对于一个空间，如果某个角落里有个盒子我们却不知道在哪儿。但是"神"可以告诉我们这个盒子在或者不在某范围内，显而易见的方法就是把空间化成8个卦限，然后询问在哪个卦限内。再将存在的卦限继续化成8个。意思大概就是太极生两仪，两仪生四象，四象生八卦，就这么一直划分下去，最后一定会确定一个非常小的空间。对于点云而言，只要将点云的立方体凸包用 octree 生成很多很多小的卦限，那么在相邻卦限里的点则为相邻点。

显然，对于不同点云应该采取不同的搜索策略。如果点云是疏散的，分布很广泛，且没什么规律（如 lidar 测得的点云或双目视觉捕捉的点云），kdTree 能更好的划分，而 octree 则很难决定最小立方体应该是多少，太大则一个立方体里可能有很多点云，太小则可能立方体之间连不起来。如果点云分布非常规整，是某个特定物体的点云模型，则应该使用 ocTree，因为很容易求解凸包并且点与点之间相对距离无需再次比对父节点和子节点，更加明晰。典型的例子是斯坦福的兔子。

二叉树：

树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。根结点：根节点没有前驱结点。除根节点外，其余结点被分成是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有0个或多个后继。因此，树是递归定义的。一棵二叉树是结点的一个有限集合，该集合或者为空，或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
二叉树的特点：

每个结点最多有两棵子树，即二叉树不存在度大于2的结点。

二叉树的子树有左右之分，其子树的次序不能颠倒。

所谓遍历(Traversal)是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，是二叉树上进行其它运算之基础。

前序/中序/后序的递归结构遍历：是根据访问结点操作发生位置命名

NLR：前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。

LNR：中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。

LRN：后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。

层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

Vector容器：

功能：vector容器的功能和数组非常相似，使用时可以把它看成一个数组

vector和普通数组的区别：

1.数组是静态的，长度不可改变，而vector可以动态扩展，增加长度

2.数组内数据通常存储在栈上，而vector中数据存储在堆上

动态扩展：(这个概念很重要)

动态扩展并不是在原空间之后续接新空间，而是找到比原来更大的内存空间，将原数据拷贝到新空间，释放原空间

注意：使用vector之前必须包含头文件 #include

Batch：

翻译成汉语为批（一批一批的批）。在神经网络模型训练时，比如有1000个样本，把这些样本分为10批，就是10个batch。每个批（batch）的大小为100，就是batch size=100。

每次模型训练，更新权重时，就拿一个batch的样本来更新权重。

SGD（stochastic gradient descent随机梯度下降）:

 

梯度下降法的基本思想可以类比为一个下山的过程。

假设这样一个场景：一个人被困在山上，需要从山上下来(找到山的最低点，也就是山谷)。但此时山上的浓雾很大，导致可视度很低；因此，下山的路径就无法确定，必须利用自己周围的信息一步一步地找到下山的路。这个时候，便可利用梯度下降算法来帮助自己下山。怎么做呢，首先以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着下降方向走一步，然后又继续以当前位置为基准，再找最陡峭的地方，再走直到最后到达最低处；同理上山也是如此，只是这时候就变成梯度上升算法了。

梯度是微积分中一个很重要的概念，之前提到过梯度的意义。在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率。在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向。α在梯度下降算法中被称作为学习率或者步长，意味着我们可以通过α来控制每一步走的距离，以保证不要步子跨的太大，其实就是不要走太快，错过了最低点。同时也要保证不要走的太慢，导致太阳下山了，还没有走到山下。所以α的选择在梯度下降法中往往是很重要的！α不能太大也不能太小，太小的话，可能导致迟迟走不到最低点，太大的话，会导致错过最低点！

梯度前加一个负号，就意味着朝着梯度相反的方向前进！我们在前文提到，梯度的方向实际就是函数在此点上升最快的方向！而我们需要朝着下降最快的方向走，自然就是负的梯度的方向，所以此处需要加上负号；那么如果时上坡，也就是梯度上升算法，当然就不需要添加负号了。

深度学习使用的训练集一般都比较大（几十万～几十亿）。而BGD算法，每走一步（更新模型参数），为了计算original-loss上的梯度，就需要遍历整个数据集，这显然是不现实的。而SGD算法，每次随机选择一个mini-batch去计算梯度，在minibatch-loss上的梯度显然是original-loss上的梯度的无偏估计，因此利用minibatch-loss上的梯度可以近似original-loss上的梯度，并且每走一步只需要遍历一个minibatch（一～几百）的数据。

SGD走的路径比较曲折（震荡），尤其是batch比较小的情况下。

解释：

为了方便说明，假设loss函数是凸函数（没有奇点，local minimal就是global minimal）。即使loss函数不是凸函数也是相同的道理。 需要记住，不管使用什么优化方法，待优化的目标都是original-loss，分析问题都要从这一点出发。

BGD每次走的方向是original-loss的负梯度方向，是original-loss在当前点上的最速下降方向。而SGD每次走的方向是minibatch-loss的负梯度方向（或者理解成original-loss的负梯度+randomness），显然这个方向和original-loss的负梯度方向不同，也就不是original-loss在当前位置的最快下降方向（如果这个mini batch的大部分数据点的target是错误的，甚至有可能是original-loss在当前位置的上升方向），所以使用SGD算法从当前点走到global minimal的路径会很曲折（震荡）。

为了减少震荡，一个方法是增大batch size，原因是minibatch-loss的梯度是对original-loss梯度的无偏估计（bias为0），并且variance随着batch size的变大而减小。当batch size足够大（比如接近训练集），此时SGD就退化成了BGD，就会带来上面说的那些问题。因此batch size需要选择合适大小，一般是几十到几百。

条件允许情况下，在使用SGD时，开始使用小batch size和大学习率，然后让batch size慢慢增加，学习率慢慢减小。

KITTI:

数据集由德国卡尔斯鲁厄理工学院和丰田美国技术研究院联合创办，是目前国际上最大的自动驾驶场景下的计算机视觉算法评测数据集。该数据集用于评测立体图像(stereo)，光流(optical flow)，视觉测距(visual odometry)，3D物体检测(object detection)和3D跟踪(tracking)等计算机视觉技术在车载环境下的性能。KITTI包含市区、乡村和高速公路等场景采集的真实图像数据，每张图像中最多达15辆车和30个行人，还有各种程度的遮挡与截断。整个数据集由389对立体图像和光流图，39.2 km视觉测距序列以及超过200k 3D标注物体的图像组成，以10Hz的频率采样及同步。总体上看，原始数据集被分类为’Road’, ’City’, ’Residential’, ’Campus’ 和 ’Person’。对于3D物体检测，label细分为car, van, truck, pedestrian, pedestrian(sitting), cyclist, tram以及misc组成。

KITTI数据集的数据采集平台装配有2个灰度摄像机，2个彩色摄像机，一个Velodyne 64线3D激光雷达，4个光学镜头，以及1个GPS导航系统。

 

PointNet：

点云实际上拥有置换不变性的特点，那么什么是置换不变性呢，简单地说就是点的排序不影响物体的性质，打乱之后表述的其实是同一个物体。因此针对点云的置换不变性，其设计的网络必须是一个对称的函数。我们经常看到的SUM和MAX等函数其实都是对称函数。因此我们可以利用max函数设计一个很简单的点云网络。但是这样的网络有一个问题，就是每个点损失的特征太多了，输出的全局特征仅仅继承了三个坐标轴上最大的那个特征，因此我们不妨先将点云上的每一个点映射到一个高维的空间（例如1024维），目的是使得再次做MAX操作，损失的信息不会那么多。此时我们发现，当我们将点云的每个点先映射到一个冗余的高维空间后，再去进行max的对称函数操作，损失的特征就没那么多了。由此，就可以设计出这PointNet的雏形，称之为PointNet(vanilla)：

点云的旋转不变性指的是，给予一个点云一个旋转，所有的x , y , z x,y,zx,y,z坐标都变了，但是代表的还是同一个物体。因此对于普通的PointNet(vanilla)，如果先后输入同一个但是经过不同旋转角度的物体，它可能不能很好地将其识别出来。在论文中的方法是新引入了一个T-Net网络去学习点云的旋转，将物体校准，剩下来的PointNet(vanilla)只需要对校准后的物体进行分类或者分割即可。

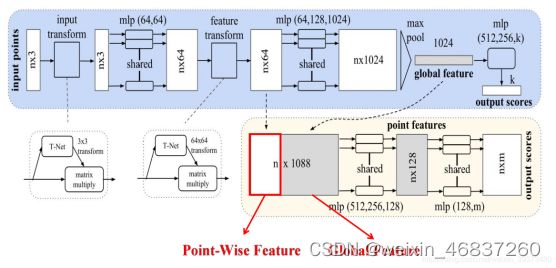
由于点云的旋转非常的简单，只需要对一个N × D N\times DN×D的点云矩阵乘以一个D × D D \times DD×D的旋转矩阵即可，因此对输入点云学习一个3 × 3 3 \times 33×3的矩阵，即可将其矫正；同样的将点云映射到K维的冗余空间后，再对K维的点云特征做一次校对，只不过这次校对需要引入一个正则化惩罚项，希望其尽可能接近于一个正交矩阵。满足了以上两个点云的特性之后，就可以顺理成章的设计出PointNet的网络结构了。具体来说，对于每一个N × 3 N\times 3N×3的点云输入，网络先通过一个T-Net将其在空间上对齐（旋转到正面），再通过MLP将其映射到64维的空间上，再进行对齐，最后映射到1024维的空间上。这时对于每一个点，都有一个1024维的向量表征，而这样的向量表征对于一个3维的点云明显是冗余的，因此这个时候引入最大池化操作，将1024维所有通道上都只保留最大的那一个，这样得到的1 × 1024 1\times 10241×1024的向量就是N NN个点云的全局特征。如果做的是分类的问题，直接将这个全局特征再进过MLP去输出每一类的概率即可；但如果是分割问题，由于需要输出的是逐点的类别，因此其将全局特征拼接在了点云64维的逐点特征上，最后通过MLP，输出逐点的分类概率。

 

pointnet当时不论是分割还是分类的结果都超过了当时的体素系列网络，同时由于参数少等特点，训练快，属于轻量级网络。

PointNet++

提出源于PointNet的缺点——缺失局部特征。

从很多实验结果都可以看出，PointNet对于场景的分割效果十分一般，由于其网络直接暴力地将所有的点最大池化为了一个全局特征，因此局部点与点之间的联系并没有被网络学习到。在分类和物体的Part Segmentation中，这样的问题还可以通过中心化物体的坐标轴部分地解决，但在场景分割中，这就导致效果十分一般了。

Multi-Scale PointNet

作者在第二代PointNet中主要借鉴了CNN的多层感受野的思想。CNN通过分层不断地使用卷积核扫描图像上的像素并做内积，使得越到后面的特征图感受野越大，同时每个像素包含的信息也越多。而PointNet++就是仿照了这样的结构，具体如下：

其先通过在整个点云的局部采样并划一个范围，将里面的点作为局部的特征，用PointNet进行一次特征的提取。因此，通过了多次这样的操作以后，原本的点的个数变得越来越少，而每个点都是有上一层更多的点通过PointNet提取出来的局部特征，也就是每个点包含的信息变多了。文章将这样的一个层成为Set Abstraction。

Set Abstraction的实现细节

一个Set Abstraction主要由三部分组成：

Sampling：利用FPS（最远点采样）随机采样点

Grouping：利用Ball Query划一个R为半径的圈，将每个圈里面的点云作为一簇

PointNet： 对Sampling+Grouping以后的点云进行局部的全局特征提取

PointNet系列基本是近两年来所有点云分割网络的baseline，大部分state-of-art的网络也是通过以这两个网络为基础构造出来的。其优点非常的明显，就是参数量小；但其缺点就是对于局部的特征的抓取还不是特别的完善，这也是未来可以改进的地方。

IOU（交并比）:

IOU就是用来度量目标检测中预测框与真实框的重叠程度。用预测框(A)和真实框(B)的交集除上二者的并集，其公式为：

I O U = A ∩ B /A ∪ B

 

鲁棒性（Robustness）:

计算机科学中，健壮性（英语：Robustness）是指一个计算机系统在执行过程中处理错误，以及算法在遭遇输入、运算等异常时继续正常运行的能力。 诸如模糊测试之类的形式化方法中，必须通过制造错误的或不可预期的输入来验证程序的健壮性。很多商业产品都可用来测试软件系统的健壮性。健壮性也是失效评定分析中的一个方面。即一个系统或组织有抵御或克服不利条件的能力。在机器学习，训练模型时，工程师可能会向算法内添加噪声（如对抗训练），以便测试算法的「鲁棒性」。可以将此处的鲁棒性理解述算法对数据变化的容忍度有多高。

鲁棒性并不同于稳定性，稳定性通常意味着「特性随时间不变化的能力」，鲁棒性则常被用来描述可以面对复杂适应系统的能力，需要更全面的对系统进行考虑。

点云配准定义：通过求解坐标转换关系，将连续扫描的两帧或多帧激光点云统一到同一坐标系（scan–to-scan），或者将当前扫描点云与以建立的地图进行配准（scan-to-map）从而最终恢复载体位置和姿态的变化。

slam配准：为了得到相对姿态变化，在实时性与精度之间取得平衡

测绘点云配准（拼接）：得到坐标系统一的点云，更注重精度

二者解决的是同一个问题。

点云配准综述：

点云配准的价值在于它在众多计算机视觉应用中的独特而关键的作用。

首先，三维重建。生成完整的三维场景是各种计算机视觉应用的基础和重要技术，包括自动驾驶中的高精度三维地图重建、机器人技术中的三维环境重建和实时监控地下采矿的三维重建。例如，点云配准可以为机器人应用中的路线规划和决策构建三维环境。另一个例子是在地下采矿空间进行大型三维场景重建，以准确监控采矿安全。

第二，三维定位。在三维环境中定位移动智能设备的位置对于机器人技术尤为重要。例如，无人驾驶汽车估计其在地图上的位置（例如<10cm）及其到道路边界线的距离。点云配准可以将当前的实时三维点云精确匹配到所属的三维环境中，提供高精度的定位服务。此应用程序表明，配准为智能系统（例如机器人或无驾驶汽车）提供了一个与3D环境交互的解决方案。

第三，姿态估计。将一个点云A（3D实时视图）与另一个点云B（3D环境）对齐，可以生成与点云B相对的点云A的姿态信息，这些姿态信息可用于机器人的决策。例如，可以获得机器人手臂的姿势信息，从而决定移动到哪里以准确地抓取对象。姿态估计应用表明，该配准方法还提供了一种了解环境中agent信息的方法。由于点云配准在许多有价值的计算机视觉应用中扮演着重要的角色，因此迫切需要对点云配准进行全面的研究，以使这些应用受益。

 

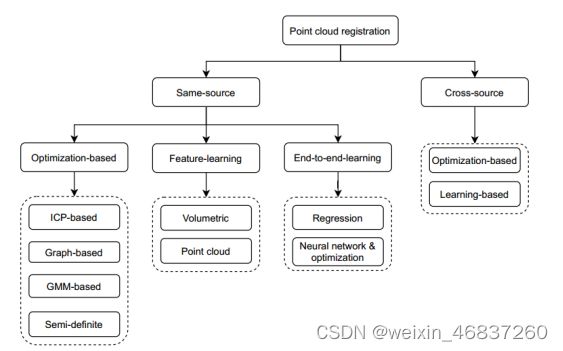
同源点云配准

同源点云的配准是指从同一类型的传感器，但在不同的时间或视角下获取的点云在进行配准问题中存在的挑战，其主要包含了

噪声和离群值。在不同的采集时间，环境和传感器噪声是不同的，采集到的点云在同一三维位置附近会包含噪声和异常值。

部分重叠。由于视点和采集时间的不同，采集到的点云只是部分重叠。

跨源点云配准

跨源点云配准的挑战，点云传感器经历了快速发展。例如，Kinect已经在许多领域得到了广泛的应用。激光雷达变得使用价格合理，并已集成到移动电话（如iPhone 12）中。而且，多年来三维重建技术的发展使得利用RGB相机生成点云成为可能。尽管在点云采集方面有这些改进，但每个传感器都有其独特的优点和局限性。例如，Kinect可以记录详细的结构信息，但视距有限；Lidar可以记录远处的物体，但分辨率有限。许多证据[77]，[41]表明，来自不同传感器的融合点云可为实际应用提供更多的信息和更好的性能。点云融合需要跨源点云配准技术。由于点云是从不同类型的传感器获取的，并且不同类型的传感器包含不同的成像机制，因此点云配准问题中的跨源挑战要比同源点云配准挑战复杂得多。这些挑战主要可以分为噪声和异常值。由于不同采集时间的采集环境、传感器噪声和传感器成像机制不同，采集到的点云在同一个三维位置附近会包含噪声和离群点。

1. 部分重叠。由于视点和采集时间的不同，采集到的点云只是部分重叠。
2. 密度差。由于不同的成像机制和不同的分辨率，捕获的点云通常包含不同的密度。
3. 尺度变化。由于不同的成像机制可能具有不同的物理度量，因此捕获的点云可能包含尺度差异。

不同类型的三维传感器的数据融合

例如，Kinect可以生成密集的点云，而测量范围通常限制为5米。激光雷达在生成稀疏点云的同时具有很长的视距。

1. 一种基于优化的点云配准框架。给定两个输入点云，迭代估计这些点云之间的对应关系和变换。算法输出最优变换T作为最终变换矩阵。
2. 基于特征学习的点云配准框架。给定两个输入点云，利用深度神经网络对特征进行估计。然后，对应和变换估计迭代运行以估计最终变换矩阵T。
3. 一个基于端到端学习的点云配准框架。给定两个输入点云，使用端到端框架来估计最终变换矩阵T。
4. 一个跨源点云配准框架。在给定两个输入点云的情况下，设计了一个配准框架来克服跨源问题并估计最终的变换矩阵T。

端到端学习

总结起来就是不经过复杂的中间建模过程，从输入端到输出端会得到一个预测的结果，这个预测的结果与标记的真实数据之间会进行计算，得到误差结果。然后我们采用比如梯度下降的方法使得误差结果减少，模型最终达到收敛，输出最终的结果，则就是端到端的学习过程。端到端的学习可以大量的减少人为标注的工作量，同时可以使得预测的结果更能符合预期的要求。

相对于深度学习，传统机器学习的流程往往由多个独立的模块组成，比如在一个典型的自然语言处理（Natural Language Processing）问题中，包括分词、词性标注、句法分析、语义分析等多个独立步骤，每个步骤是一个独立的任务，其结果的好坏会影响到下一步骤，从而影响整个训练的结果，这是非端到端的。

而深度学习模型在训练过程中，从输入端（输入数据）到输出端会得到一个预测结果，与真实结果相比较会得到一个误差，这个误差会在模型中的每一层传递（反向传播），每一层的表示都会根据这个误差来做调整，直到模型收敛或达到预期的效果才结束，这是端到端的。

两者相比，端到端的学习省去了在每一个独立学习任务执行之前所做的数据标注，为样本做标注的代价是昂贵的、易出错的。

独热编码One-Hot编码：

又称为一位有效编码，主要是采用位状态寄存器来对个状态进行编码，每个状态都有他独立的寄存器位，并且在任意时候只有一位有效。

独热编码 是利用0和1表示一些参数，使用N位状态寄存器来对N个状态进行编码。

例如：参考数字手写体识别中：如数字字体识别0~9中，6的独热编码为0000001000

自然状态码为：000,001,010,011,100,101

独热编码为：000001,000010,000100,001000,010000,100000

有如下三个特征属性：

性别：["male"，"female"] ======》[1，0] 表示男，[0，1]表示女

地区：["Europe"，"US"，"Asia"]

浏览器：["Firefox"，"Chrome"，"Safari"，"Internet Explorer"]

对于某一个样本，如["male"，"US"，"Internet Explorer"]，我们需要将这个分类值的特征数字化，最直接的方法，我们可以采用序列化的方式：[0,1,3]。但是这样的特征处理并不能直接放入机器学习算法中。

 对于上述的问题，性别的属性是二维的，同理，地区是三维的，浏览器则是思维的，这样，我们可以采用One-Hot编码的方式对上述的样本“["male"，"US"，"Internet Explorer"]”编码，“male”则对应着[1，0]，同理“US”对应着[0，1，0]，“Internet Explorer”对应着[0,0,0,1]。则完整的特征数字化的结果为：[1,0,0,1,0,0,0,0,1]。这样导致的一个结果就是数据会变得非常的稀疏。

优点

独热编码的优点为：

1.能够处理非连续型数值特征。

2.在一定程度上也扩充了特征。比如性别本身是一个特征，经过one hot编码以后，就变成了男或女两个特征。

当然，当特征类别较多时，数据经过独热编码可能会变得过于稀疏。

实现

from sklearn import preprocessing

encoder = preprocessing.OneHotEncoder()

# 4个特征：

#第一个特征（即为第一列）为[0,1,2,1],其中三类特征值[0,1,2],因此One-Hot Code可将[0,1,2]表示为:[100,010,001]

#第一个特征有三种值：采用三个编码：[100,010,001]

#同理第二个特征列可将两类特征值[2,3]表示为[10,01]

#第三个特征将4类特征值[1,2,4,5]表示为[1000,0100,0010,0001]

#第四个特征将2类特征值[3,12]表示为[10,01]

encoder.fit([

    [0, 2, 1, 12],

    [1, 3, 5, 3],

    [2, 3, 2, 12],

    [1, 2, 4, 3]

])

encoded_vector = encoder.transform([[2, 3, 5, 3]]).toarray()

print("\n Encoded vector =", encoded_vector)

#[[0. 0. 1.    0. 1.      0. 0. 0. 1.     1. 0.]]

交叉熵（cross entropy）：

是深度学习中常用的一个概念，一般用来求目标与预测值之间的差距。交叉熵是信息论中的一个概念，当越不可能的事件发生了，我们获取到的信息量就越大。越可能发生的事件发生了，我们获取到的信息量就越小。那么信息量应该和事件发生的概率有关。熵用来表示所有信息量的期望。

相对熵又称KL散度,如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x)，我们可以使用 KL 散度（Kullback-Leibler (KL) divergence）来衡量这两个分布的差异。在机器学习中，P往往用来表示样本的真实分布，比如[1,0,0]表示当前样本属于第一类。Q用来表示模型所预测的分布，比如[0.7,0.2,0.1]

直观的理解就是如果用P来描述样本，那么就非常完美。而用Q来描述样本，虽然可以大致描述，但是不是那么的完美，信息量不足，需要额外的一些“信息增量”才能达到和P一样完美的描述。如果我们的Q通过反复训练，也能完美的描述样本，那么就不再需要额外的“信息增量”，Q等价于P。

在机器学习中，我们需要评估label和predicts之间的差距，使用KL散度刚刚好，即DKL(y||y^)DKL(y||y^)，由于KL散度中的前一部分−H(y)−H(y)不变，故在优化过程中，只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss，评估模型。

线性回归：

就是在N维空间中找一个形式像直线方程一样的函数来拟合数据而已

TensorFlow：

Tensor，也就是“张量”，张量=容器。张量是现代机器学习的基础。它的核心是一个数据容器，多数情况下，它包含数字，有时候它也包含字符串，但这种情况比较少。因此把它想象成一个数字的水桶。张量在0维到5维之间。装在张量/容器水桶中的每个数字称为“标量”。标量是一个数字。

 

int main(int argc, char* argv[])：

main的形参只有二个，而命令行中的参数个数原则上未加限制。argc参数表示了命令行中参数的个数(注意：文件名本身也算一个参数)，argc的值是在输入命令行时由系统按实际参数的个数自动赋予的。argv[ ]是argc个参数，其中第0个参数是程序的全名，命令行后面跟的用户输入的参数，比如：C:\>可执行文件名 参数 参数……

去除NaN点：
pcl::removeNaNFromPointCloud(laserCloudIn, laserCloudIn, indices);

函数有三个参数，分别为输入点云，输出点云及对应保留的索引。

std::vector indices;

pcl::removeNaNFromPointCloud(laserCloudIn, laserCloudIn, indices);

cerr ：

是一个ostream对象，关联到标准错误，通常写入到与标准输出相同的设备。默认情况下，写到cerr的数据是不缓冲的。cerr通常用于输出错误信息与其他不属于正常逻辑的输出内容。cerr对应标准错误流，用于显示错误消息。默认情况下被关联到标准输出流，但它不被缓冲，也就说错误消息可以直接发送到显示器，而无需等到缓冲区或者新的换行符时，才被显示。一般情况下不被重定向。

程序遇到调用栈用完了的威胁（无限，没有出口的递归）。
你说，你到什么地方借内存，存放你的错误信息？所以有了cerr。其目的，就是在你最需要它的紧急情况下，还能得到输出功能的支持。缓冲区的目的，就是减少刷屏的次数.

size_t和int:

 size_t是一些C/C++标准在stddef.h中定义的。这个类型足以用来表示对象的大小。size_t的真实类型与操作系统有关。

在32位架构中被普遍定义为：typedef   unsigned int size_t;

而在64位架构中被定义为：typedef  unsigned long size_t;

size_t在32位架构上是4字节，在64位架构上是8字节，在不同架构上进行编译时需要注意这个问题。而int在不同架构下都是4字节，与size_t不同；且int为带符号数，size_t为无符号数。

为什么有时候不用int，而是用size_type或者size_t:

与int固定四个字节不同有所不同,size_t的取值range是目标平台下最大可能的数组尺寸,一些平台下size_t的范围小于int的正数范围,又或者大于unsigned int. 使用Int既有可能浪费，又有可能范围不够大。

滤波器：

球形滤波器RadiusOutlinerRemoval比较适合去除单个的离群点

条件滤波器ConditionalRemoval 比较灵活，可以根据用户设置的条件灵活过滤

直通滤波器 PassThrough直接指定保留哪个轴上的范围内的点

均匀采样：半径求体内 保留一个点（重心点）UniformSampling

统计滤波器用于去除明显离群点StatisticalOutlierRemoval

投影滤波　输出投影后的点的坐标

模型滤波器

体素格 （正方体立体空间内 保留一个点（重心点））VoxelGrid

pcl::PCLPointCloud2：

是 ROS（机器人操作系统）消息类型，取代旧的 sensors_msgs::PointCloud2。因此，它只能在与 ROS 进行交互时使用。

// 从 PCLPointCloud2 转化为 PointCloud

void fromPCLPointCloud2(const pcl::PCLPointCloud2& msg, pcl::PointCloud& cloud);

// 内部调用 fromPCLPointCloud2 函数

void fromROSMsg (const pcl::PCLPointCloud2& msg, pcl::PointCloud& cloud);

      

// 从 PointCloud 转化为 PCLPointCloud2

void toPCLPointCloud2(const pcl::PointCloud& cloud, pcl::PCLPointCloud2& msg);

// 内部调用 toPCLPointCloud2 函数

void toROSMsg (const pcl::PointCloud& cloud, pcl::PCLPointCloud2& msg);

光流

光流：像素在不同图像间的运动

除了提供远近外，还可以提供角度信息。与咱们的眼睛正对着的方向成90度方向运动的物体速度要比其他角度的快，当小到0度的时候，也就是物体朝着我们的方向直接撞过来，我们就是感受不到它的运动（光流）了，看起来好像是静止的。当它离我们越近，就越来越大（当然了，我们平时看到感觉还是有速度的，因为物体较大，它的边缘还是和我们人眼具有大于0的角度的）。

       光流的概念是Gibson在1950年首先提出来的。它是空间运动物体在观察成像平面上的像素运动的瞬时速度，是利用图像序列中像素在时间域上的变化以及相邻帧之间的相关性来找到上一帧跟当前帧之间存在的对应关系，从而计算出相邻帧之间物体的运动信息的一种方法。一般而言，光流是由于场景中前景目标本身的移动、相机的运动，或者两者的共同运动所产生的。

假设条件

（1）亮度恒定，就是同一点随着时间的变化，其亮度不会发生改变。这是基本光流法的假定（所有光流法变种都必须满足），用于得到光流法基本方程；

（2）小运动，这个也必须满足，就是时间的变化不会引起位置的剧烈变化，这样灰度才能对位置求偏导（换句话说，小运动情况下我们才能用前后帧之间单位位置变化引起的灰度变化去近似灰度对位置的偏导数），这也是光流法不可或缺的假定；

（3）空间一致，一个场景上邻近的点投影到图像上也是邻近点，且邻近点速度一致。这是Lucas-Kanade光流法特有的假定，因为光流法基本方程约束只有一个，而要求x，y方向的速度，有两个未知变量。我们假定特征点邻域内做相似运动，就可以连立n多个方程求取x，y方向的速度（n为特征点邻域总点数，包括该特征点）。

目前，对光流的研究方兴未艾，新的计算方法还在不断涌现。这里对光流技术的发展趋势与方向提出以下几点看法：

(1)现有技术各有自己的优点与缺陷，方法之间相互结合，优势互补，建立光流计算的多阶段或分层模型，是光流技术发展的一个趋势;

(2)通过深入的研究发现，现有光流方法之间有许多共通之处。如微分法和匹配法的前提假设极为相似；某些基于能量的方法等效于区域匹配技术；而相位方法则将相位梯度用于法向速度的计算。这些现象并不是偶然的。Singh指出，现有各种光流估计方法基本上可以统一在一个框架之中，这个框架将光流信息分成两类：保持信息和邻域信息，光流场的恢复通过两种信息的提取和融合来实现。光流计算的统一框架的研究是这个领域的又一趋势；

(3)尽管光流计算的神经动力学方法还很不成熟，然而对它的研究却具有极其深远的意义。随着生物视觉研究的不断深入，神经方法无疑会不断完善，也许光流计算乃至计算机视觉的根本出路就在于神经机制的引入。神经网络方法是光流技术的一个发展方向。

Lucas-Kanade是一种广泛使用的光流估计的差分方法，这个方法是由Bruce D. Lucas和Takeo Kanade发明的。它假设光流在像素点的邻域是一个常数，然后使用最小二乘法对邻域中的所有像素点求解基本的光流方程。

通过结合几个邻近像素点的信息，卢卡斯-金出方法(简称为L-K方法)通常能够消除光流方程里的多义性。而且，与逐点计算的方法相比，L-K方法对图像噪声不敏感。不过，由于这是一种局部方法，所以在图像的均匀区域内部，L-K方法无法提供光流信息。