机器学习历程——人工智能基础与应用导论（4）（线性模型——实战）

一、线性回归模型：以scikit-learn自带糖尿病人问题为例研究

1、引入库

# 导入所需包包
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model,discriminant_analysis,model_selection

2、加载数据

# 加载数据集(scikit-learn自带糖尿病人的数据集)
def load_data1(): #随机将数据分为两部分
    diabetes = datasets.load_diabetes()
    return model_selection.train_test_split(diabetes.data,diabetes.target,
                                             test_size=0.35,random_state=0) #test_size——测试集所占数据比例，random_state——随机种子，确保每次划分一致
# 返回元组值为：训练样本集、测试样本集、训练样本集对应的标签值、测试样本集对应的标签值

3、LinearRegression模型

def test_LinearRegression(*data):
    X_train, X_test, y_train, y_test=data #X训练集、X测试集、Y训练集、Y测试集
    regr = linear_model.LinearRegression() #引入线性模型
    regr.fit(X_train, y_train) #训练模型
    print('Coefficients:%s, intercept %.2f'%(regr.coef_,regr.intercept_)) #权重向量：.coef_，b值.intercept_
#？？？？？
    print("Residual sum of squares:%.2f"% np.mean((regr.predict(X_test)-y_test)**2)) #残差平方和RSS
    print('Score:%.2f'%regr.score(X_test,y_test)) #预测性能得分

4、调用函数 

X_train, X_test, y_train, y_test=load_data1()
test_LinearRegression(X_train, X_test, y_train, y_test)

 5、结果如下：

Coefficients:[ -64.91368307 -194.87471389  572.02842585  323.3507952  -682.6160746
  344.30645136   68.52556572  145.33490249  800.49553329   41.24031916], intercept 152.18
Residual sum of squares:3214.18
Score:0.40

二、逻辑回归：以系统自带鸢尾花问题为例研究

1、LogisticRegression模型

2、预测代码

# 加载鸢尾花数据
def load_data2():
    iris=datasets.load_iris()
    X_train=iris.data #X取值
    y_train=iris.target #y取值
    return model_selection.train_test_split(X_train,y_train,
                                              test_size=0.25,random_state=0,stratify=y_train)
# 将stratify=X就是按照X中的比例分配
# 将stratify=y就是按照y中的比例分配

# 模型训练
def test_LogisticRegression(*data):
    X_train, X_test, y_train, y_test=data
    regr = linear_model.LogisticRegression() #引入模型
    regr.fit(X_train, y_train) #训练
    print('Coefficients:%s, intercept %.2f'%(regr.coef_,regr.intercept_)) #权重向量、b值
    print("Residual sum of squares:%.2f"% np.mean((regr.predict(X_test)-y_test)**2)) #RSS
    print('Score:%.2f'%regr.score(X_test,y_test)) #得分

# 应用
X_train, X_test, y_train, y_test=load_data2()
# 此处代码有误，待我问问老师，如果有大佬看出原因，欢迎指出呀
test_LinearRegression(X_train, X_test, y_train, y_test)

报错了，目前我还没有解决，解决了会第一时间修改代码。

TypeError: only size-1 arrays can be converted to Python scalars

3、利用正则C，画图

# C——指定了罚项系数的倒数，值越小，正则化项越大
def test_LogisticRegression_C(*data):
    X_train, X_test, y_train, y_test=data
    Cs=np.logspace(-2,4,num=100) #用于创建等比数列，默认10的多少次幂，base可修改底数
    scores=[]
    for C in Cs:
        regr = linear_model.LogisticRegression(C=C,max_iter=1000) #最大迭代次数：max_iter
        regr.fit(X_train, y_train) #训练
        scores.append(regr.score(X_test, y_test)) #得分
    ##画图：plot
    fig=plt.figure() #建画布
    ax=fig.add_subplot(1,1,1) #划分画布
    ax.plot(Cs,scores) #横纵轴
    ax.set_xlabel(r"C") #X图例
    ax.set_ylabel(r"score") #Y 图例
    ax.set_xscale('log') #使用 set_xscale () 或 set_yscale () 函数分别设置 X 轴和 Y 轴的缩放比例。
    ax.set_title("LogisticRegression") #标题
    plt.show() #展示
    
X_train, X_test, y_train, y_test=load_data2()
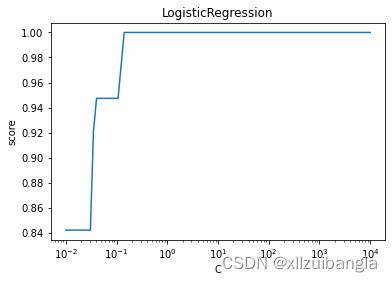
test_LogisticRegression_C(X_train, X_test, y_train, y_test)

测试结果如下图所示。可以看到随着C的增大(即正则化项减小)，LogisticRegression的
预测准确率上升。当C增大到一定程度(即正则化项减小到一定程度)，LogisticRegression的
预测准确率维持在较高的水准保持不变。

 

四、线性判别回归：以系统自带鸢尾花问题为例研究

1、LinearDiscriminantAnalysis

 2、代码

# 加载鸢尾花数据
def load_data2():
    iris=datasets.load_iris()
    X_train=iris.data #X取值
    y_train=iris.target #y取值
    return model_selection.train_test_split(X_train,y_train,test_size=0.25,random_state=0,stratify=y_train)

# 模型
def test_LinearDiscriminantAnalysis(*data):
    X_train, X_test, y_train, y_test=data
    lda = discriminant_analysis.LinearDiscriminantAnalysis()
    lda.fit(X_train, y_train)
    print('Coefficients:%s, intercept %s'%(lda.coef_,lda.intercept_))
    print("Residual sum of squares:%.2f"% np.mean((lda.predict(X_test)-y_test)**2))
    print('Score:%.2f'%lda.score(X_test,y_test))

# 应用
X_train, X_test, y_train, y_test=load_data2()
test_LinearDiscriminantAnalysis(X_train, X_test, y_train, y_test)   

3、测试结果

对测试集的预测准确率为1.0，说明LinearDiscriminantAnalysis对于册书籍的预测完全正确。

Coefficients:[[  6.66775427   9.63817442 -14.4828516  -20.9501241 ] [ -2.00416487  -3.51569814   4.27687513   2.44146469] [ -4.54086336  -5.96135848   9.93739814  18.02158943]], intercept [-15.46769144   0.60345075 -30.41543234]
Residual sum of squares:0.00
Score:1.00

 4、绘制LDA降维之后数据集的函数

检查原始数据在经过线性判别分析后LDS之后的数据集的情况。

# 加载鸢尾花数据
def load_data2():
    iris=datasets.load_iris()
    X_train=iris.data #X取值
    y_train=iris.target #y取值
    return model_selection.train_test_split(X_train,y_train,
                                              test_size=0.25,random_state=0,stratify=y_train)

def test_LinearDiscriminantAnalysis(*data):
    X_train, X_test, y_train, y_test=data
    lda = discriminant_analysis.LinearDiscriminantAnalysis()
    lda.fit(X_train, y_train)
    print('Coefficients:%s, intercept %s'%(lda.coef_,lda.intercept_))
    print("Residual sum of squares:%.2f"% np.mean((lda.predict(X_test)-y_test)**2))
    print('Score:%.2f'%lda.score(X_test,y_test))

X_train, X_test, y_train, y_test=load_data2()
test_LinearDiscriminantAnalysis(X_train, X_test, y_train, y_test)   

# LDA
def plot_LDA(converted_X,y):
    from mpl_toolkits.mplot3d import Axes3D #引用3D作图库
    fig=plt.figure()
    ax=Axes3D(fig) #建立3D图
    colors='rgb' #颜色
    markers='o*s' #图标
    #利用循环画出各类数据
    for target,color,marker in zip([0,1,2],colors,markers):
        pos=(y==target).ravel()
        X=converted_X[pos,:]
        ax.scatter(X[:,0],X[:,1],X[:,2],color=color,marker=marker,
                    label="label %d"%target)
    ax.legend(loc="best") #显示图例
    fig.suptitle("Iris After LDA") #标题
    plt.show()

# 应用
X_train, X_test, y_train, y_test=load_data2()
X=np.vstack((X_train, X_test)) # 垂直(行)按顺序堆叠数组
Y=np.hstack((y_train,y_test)) # 水平(列)按顺序堆叠数组
lda = discriminant_analysis.LinearDiscriminantAnalysis()
lda.fit(X, Y)
converted_X=np.dot(X,np.transpose(lda.coef_))+lda.intercept_
plot_LDA(converted_X,Y)

5、测试结果

不同鸢尾花之间的间隔较远，相同种类的鸢尾花之间相互聚集。

6、solver对预测性能影响

# solver：指定求解最优化问题的方法
# 'svd'：奇异值分解
# 'lsqr'：最小平方差算法
# 'eigen'：特征值分解算法
def test_LinearDiscriminantAnalysis_solver(*data):
    X_train, X_test, y_train, y_test=data
    solvers=['svd','lsqr','eigen']
    for solver in solvers:
        if(solver=='svd'):
            lda = discriminant_analysis.LinearDiscriminantAnalysis(solver=solver)
        else:
            lda = discriminant_analysis.LinearDiscriminantAnalysis(solver=solver,shrinkage=None)
        lda.fit(X_train, y_train)
        print('Score at solver=%s: %.2f' %(solver, lda.score(X_test, y_test)))
            
X_train, X_test, y_train, y_test=load_data2()
test_LinearDiscriminantAnalysis_solver(X_train, X_test, y_train, y_test)    

测试结果如下，三者没有差别。

 Score at solver=svd: 1.00
Score at solver=lsqr: 1.00
Score at solver=eigen: 1.00

7、引入抖动

最后考察在solver=lsqr中引入抖动。引入抖动相当于引入了正则化项。给出测试函数为：

def test_LinearDiscriminantAnalysis_shrinkage(*data):
    X_train,X_test,y_train,y_test=data
    shrinkages=np.linspace(0.0,1.0,num=20)
    scores=[]
    for shrinkage in shrinkages:
        lda = discriminant_analysis.LinearDiscriminantAnalysis(solver='lsqr',shrinkage=shrinkage)
        lda.fit(X_train, y_train)
        scores.append(lda.score(X_test, y_test))
        ## 绘图
        fig=plt.figure()
        ax=fig.add_subplot(1,1,1)
        ax.plot(shrinkages,scores)
        ax.set_xlabel(r"shrinkage")
        ax.set_ylabel(r"score")
        ax.set_ylim(0,1.05)
        ax.set_title("LinearDiscriminantAnalysis")
        plt.show()

 
# 调用该函数
X_train,X_test,y_train,y_test=load_data2()
test_LinearDiscriminantAnalysis_shrinkage(X_train,X_test,y_train,y_test)

测试结果如下图所示。可以发现随着shrinkage的增大，模型的预测准确率会随之下降。