SoundTouch变调编译以及算法代码详解
1. ubuntu20编译
源码地址:https://codeberg.org/soundtouch/soundtouch
-
安装必要依赖
sudo apt-get install automake autoconf libtool build-essential -
安装编译
cd soundtouch ./bootstrap ./configure make sudo make install
2. 改变音高测试程序使用
安装成功后,会有一个soundstretch可执行程序:
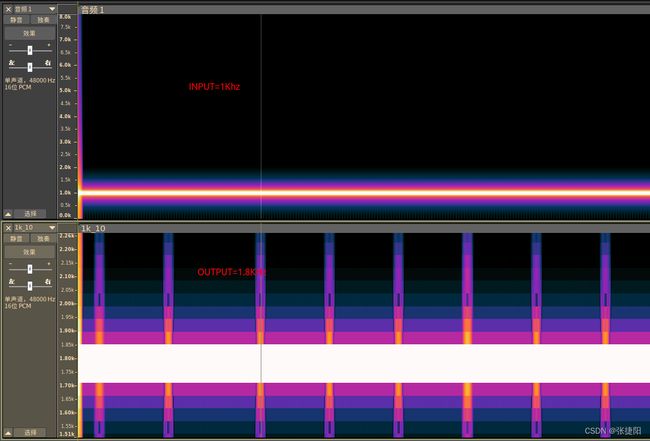
验证改变音高效果:
soundstretch input.wav output.wav -pitch=10 # 音调提升10个半音
注意这里-pitch后面跟着的n的单位为半音,半音类似分贝,是一个倍数单位。一个半音是1.06倍,因此10个半音是 1.0 6 10 = 1.79 1.06^{10} = 1.79 1.0610=1.79;因此,1khz纯音输入的话,将会输出1.8khz的纯音音频文件。
3. 算法以及代码解析
3.1. TDStretch模块(变速不变调)
3.1.0. 代码参数解析
| 参数名 | 参数含义 | 备注说明 |
|---|---|---|
| sampleRate | 输入信号以及输出信号的采样率 | |
| sequenceMS | 解析以及重组时,一帧信号的时长,单位为ms | |
| seekWindowLength | 解析以及重组时,一帧信号的采样点个数 | |
| overlapMS | 重组信号时,相邻两帧信号的重叠部分时长,单位为ms | |
| overlapLength | 重组信号时,相邻两帧信号的重叠部分的采样点个数 | |
| sampleReq | 运行WSOLA算法需要的采样点个数 | |
| intskip | 理论上,输入信号解析分帧的间隔 | |
| seekWindowMs | 检索最佳帧的范围,单位为毫秒 | |
| seekLength | 检索最佳帧的范围,单位为采样点 |
3.1.1. tempo(速率)
测试程序如果只改变了音高,速率还是保持1;但是设置到TDStretch模块中的tempo不会是1,而是 1 / (音高改变的比例),举个例子:
音高提升1.79倍,那么TDStretch中的速率将会由默认的1降低到(1 / 1.79 = 0.56)。即就是速率为原始音频的0.56;
直观上也很好理解,音高提升了1.79倍是通过将原始数据重采样到原来时长的(1/1.79)来实现的;重采样的音频需要保持和原始音频相同的时长,因此TDStretch模块需要将音频在不改变频率的前提下,慢速播放来延长音频。
3.1.2. 重叠长度(overlap length)
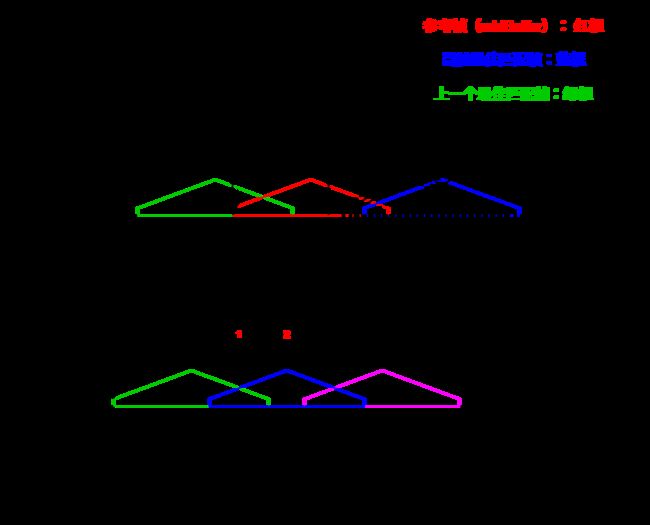
原始信号解析分帧后,需要进行重组叠加回信号流。overlap length为重组时,相邻信号的重叠长度。可以看到图1的示意图中的overlap标识。
代码中,默认的重叠长度设置为8ms的采样点个数。
3.1.3. 帧长(seekWindowLength)
3.1.4. 解析帧间隔()
3.1.5. 参考帧
如图1所示,红色帧表示参考帧。参考帧的头overlap长度的信号和其左侧的解析帧的尾部overlap长度的信号完美衔接。因此,如果以参考帧作为参考波形,在下一个解析帧附近找到其头部overlap部分和参考帧头部overlap部分最为类似的的帧。那么可以考虑将该帧作为用于重组的下一帧信号。
在代码中,参考帧的数据储存在midBuffer数组中,和图1不同的是midBuffer储存的长度不是一帧信号的长度,而是一个overlap的长度。原因在于,我们只关心参考帧前面的overlp部分(前面的overlap部分和上一个分析帧的尾部overlap部分完美衔接)。
TDStretch.cpp中给出midBuufer的赋值方式:
temp = (seekWindowLength - overlapLength); // 帧长 - 交错
memcpy(pMidBuffer, inputBuffer.ptrBegin() + channels * (offset + temp),
channels * sizeof(SAMPLETYPE) * overlapLength);
结合图1来理解,绿框是上一轮算法迭代得到的最佳匹配帧。pMidBuffer的赋值是发生在上一轮迭代中,找到最佳匹配帧之后。此时,pInputBuffer指向图1中原点位置,offset表示最佳帧(绿框)和pInputBuffer的偏移量(offset始终向右查找,其值大于等于0)。已经知道了最佳匹配帧和用于下一轮迭代的参考帧的偏移量为(帧长seekWindowLength-重叠量overlap),那么pMidBuffer将指向pInputBuffer+offset+(seekWindowLength - overlapLength);在查找最佳匹配帧的时候,我们只关心候选帧和参考帧pMidBuffer的头部overlapLength长度的相似程度。因此pMidbuffer中,只储存overlapLength长度的采样点数据。
3.1.6. 完成一次wsola算法迭代需要的数据量(sampleReq)
首先给出源码中计算sampleReq的代码:
sampleReq = max(intskip + overlapLength, seekWindowLength) + seekLength;
intskip表示分析帧间隔,overlapLength表示组合帧时相邻两帧重叠区域,seekWindowLength表示一帧信号的采样点个数,seekLength表示检索区域的长度。
完成一次算法迭代需要输出哪些数据?总结下来一共有两个点需要满足:一个是要填充MidBuffer作为下一次迭代的参考帧信号;另一个就是要确保有足够的候选区域来和当前迭代的参考帧信号进行相似度运算,从而得到最佳匹配帧。
3.1.7. outputBuffer以及相加策略
重叠相加是计算重组后信号的关键点。重叠相加主要流程是将上一个候选帧的尾部overlenLength长度的信号和当前候选帧的头部overlapLength长度的信号先加窗再相加。
源码中重叠相加在函数overlap中,这里分析一下单通道的处理函数overlapMono:
// Overlaps samples in 'midBuffer' with the samples in 'pInput'
void TDStretch::overlapMono(SAMPLETYPE *pOutput, const SAMPLETYPE *pInput) const
{
int i;
SAMPLETYPE m1, m2;
m1 = (SAMPLETYPE)0;
m2 = (SAMPLETYPE)overlapLength;
for (i = 0; i < overlapLength ; i ++)
{
pOutput[i] = (pInput[i] * m1 + pMidBuffer[i] * m2 ) / overlapLength;
m1 += 1;
m2 -= 1;
}
}
可以看出循环长度是overlapLength,将pInput的数据和pMidBuffer指向的数据重叠相加。结合流程图来分析此刻pMidBuffer以及pInput指向的位置。pMidBuffer指向的是上一帧候选信号的尾部往前overlap的位置。而这里的pInput指向的是当前候选信号的头部。因此,将两者重叠相加再放置在outputBuffer中即可。
重叠相加的方式。根据代码来看,当前候选帧的头部被一个线性上升的,斜率为(1 / overlapLength)的直线加权;而上一个候选帧被一个线性下降,斜率为( - 1 / overlapLength)的直线所加权。加权后的信号累加得到结果信号。
从代码也可以看出,重叠相加前pOutput指向上一个候选帧尾部往前overlapLength的位置。然而重叠相加后,pOutput指向的是候选帧头部往后overlapLength的位置。因此应当继续向outputBuffer填充当前候选帧的数据,填充的长度为(一帧信号长度seekWindowLength - 2 × overlapLength),该步骤在processSamples函数中实现:
outputBuffer.putSamples(inputBuffer.ptrBegin() + channels * (offset + overlapLength), (uint)(seekWindowLength - 2 * overlapLength));
3.1.8. 输入缓冲:inputBuffer
每一次迭代WSOLA算法的开始,都会确保pInputBuffer指向
开源代码实现WSOLA算法时,固定分析帧的重组间隔,接着根据tempo参数确定时长转换比例来确定对输入的原始信号的分帧间隔。重组间隔可以固定为整数。
3.2. RateTransposer模块
3.2.1. cubic插值算法(https://www.paulinternet.nl/?page=bicubic)
一个自变量为x的函数。如果已知函数值在x=0, x=1的函数值,那么我们可以用一个三阶的多项式来拟合在定义域[0, 1]之间的函数。将[0, 1]之间的任意值代入该拟合函数,即可得到估计的插值。该方法成为cubic interpolation.
一个三阶的多项式以及其一次导可以写为:
f ( x ) = a x 3 + b x 2 + c x + d f(x) = ax^3+bx^2+cx+d f(x)=ax3+bx2+cx+d
f ′ ( x ) = 3 a x 2 + 2 b x + c f'(x) = 3ax^2+2bx+c f′(x)=3ax2+2bx+c
那么在x=0, x=1处,它们的值以及导数可以表示为:
f ( 0 ) = d f(0) = d f(0)=d
f ( 1 ) = a + b + c + d f(1)=a+b+c+d f(1)=a+b+c+d
f ′ ( 0 ) = c f'(0)=c f′(0)=c
f ′ ( 1 ) = 3 a + 2 b + c f'(1)=3a+2b+c f′(1)=3a+2b+c
那么基于x=0, x=1的值以及导数,我们可以得到三次多项式的系数:
a = 2 f ( 0 ) − 2 f ( 1 ) + f ′ ( 0 ) + f ′ ( 1 ) a = 2f(0)-2f(1)+f'(0)+f'(1) a=2f(0)−2f(1)+f′(0)+f′(1)
b = − 3 f ( 0 ) + 3 f ( 1 ) − 2 f ′ ( 0 ) − f ′ ( 1 ) b = -3f(0)+3f(1)-2f'(0)-f'(1) b=−3f(0)+3f(1)−2f′(0)−f′(1)
c = f ′ ( 0 ) c = f'(0) c=f′(0)
d = f ( 0 ) d = f(0) d=f(0)
因此,如果我们能够估计0点以及1点处的导数,那么就可以得到三阶多项式的系数。插值通常用于在一系列已知采样点之间估计非采样时刻的值。我们可以假设每一个采样点的导数都为0,但是用前一个点和后一个点连线的斜率来近似该点的导数会更加平滑。
假设已知了 f ( − 1 ) = p 0 , f ( 0 ) = p 1 , f ( 1 ) = p 2 , f ( 2 ) = p 3 f(-1)=p_0, f(0) = p_1, f(1) = p_2, f(2) = p_3 f(−1)=p0,f(0)=p1,f(1)=p2,f(2)=p3,那么通过上述方式就可以得到x=0, x=1时刻的值以及导数:
f ( 0 ) = p 1 f(0)=p_1 f(0)=p1
f ( 1 ) = p 2 f(1)=p_2 f(1)=p2
f ′ ( 0 ) = p 2 − p 0 2 f'(0)=\frac{p_2-p_0}{2} f′(0)=2p2−p0
f ′ ( 1 ) = p 3 − p 1 2 f'(1)=\frac{p_3-p_1}{2} f′(1)=2p3−p1
将值带入计算三阶多项式系数的公式中,得到:
a = − 1 2 p 0 + 3 2 p 1 − 3 2 p 2 + 1 2 p 3 a = -\frac{1}{2}p_0+\frac32p_1-\frac32p_2+\frac12p_3 a=−21p0+23p1−23p2+21p3
b = p 0 − 5 2 p 1 + 2 p 2 − 1 2 p 3 b=p_0-\frac52p_1+2p_2-\frac12p_3 b=p0−25p1+2p2−21p3
c = − 1 2 p 0 + 1 2 p 2 c=-\frac12p_0+\frac12p_2 c=−21p0+21p2
d = p 1 d=p_1 d=p1
得到了多项式系数,那么就可计算[0, 1]之间的估计值:
f ( x ) = ( − 1 2 p 0 + 3 2 p 1 − 3 2 p 2 + 1 2 p 3 ) x 3 + ( p 0 − 5 2 p 1 + 2 p 2 − 1 2 p 3 ) x 2 + ( − 1 2 p 0 + 1 2 p 2 ) x + p 1 = ( − 1 2 x 3 + x 2 − 1 2 x ) p 0 + ( 3 2 x 3 − 5 2 x 2 + 1 ) p 1 + ( − 3 2 x 3 + 2 x 2 + 1 2 x ) p 2 + ( 1 2 x 3 − 1 2 x 2 ) p 3 \begin{aligned} f(x)&=(-\frac{1}{2}p_0+\frac32p_1-\frac32p_2+\frac12p_3)x^3+(p_0-\frac52p_1+2p_2-\frac12p_3)x^2+(-\frac12p_0+\frac12p_2)x+p_1\\ &=(-\frac{1}{2}x^3+x^2-\frac12x)p_0+(\frac32x^3-\frac52x^2+1)p_1+(-\frac32x^3+2x^2+\frac12x)p_2+(\frac12x^3-\frac12x^2)p_3 \end{aligned} f(x)=(−21p0+23p1−23p2+21p3)x3+(p0−25p1+2p2−21p3)x2+(−21p0+21p2)x+p1=(−21x3+x2−21x)p0+(23x3−25x2+1)p1+(−23x3+2x2+21x)p2+(21x3−21x2)p3