遗传算法的Python实现(非线性函数优化问题为例)
1、遗传算法(GA)介绍
遗传算法(Genetic Algorithm,GA)最早是由美国的 John holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出的,是一种通过模拟自然进化过程搜索最优解的方法。
该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果。遗传算法已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。
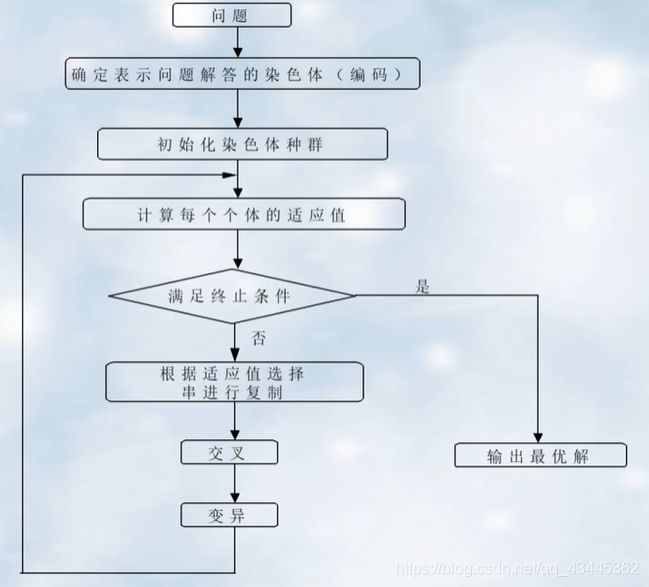
(一)遗传算法流程:
(二)基本操作:
(1)编码
- 用于将要解答的问题编码成染色体信息,便于后续运算
- 编码方式:
- 位串编码(二进制/Gray编码,存在搜索效率低的问题)
- 实数编码(较为常用)
(2)适应度函数的尺度变换
- 欺骗问题:函数值之间的差异太小,导致过早收敛
- 解决方案:尺度变换
- 线性变换(f’ = af + b)
- 幂函数变换(f’ = f ^ k)
- 指数变换(f’ = e ^ (-af))
(3)选择
- 根据适应度进行染色体串的选择,适应度越高的染色体串被选上的概率越大(不是一定选上,可以解决牛顿下降法容易收敛到局部最优的缺点)
- 个体选择的概率分配方法
- 适应度比例(蒙特卡洛法):个体适应度 / 总体适应度之和
- 排序法:分为线性排序和指数排序,后者可以扩大排名在前和在后的个体间的差距
(4)交叉
- 对两条染色体进行交叉操作
- 基本的交叉算子
- 一点交叉:选择一个位点,将两条染色体在该位点后的片段进行交叉
- 两点/多点交叉:选择多个位点,将位点间的片段进行交叉
- 部分匹配交叉:用于旅行商问题等
(5)变异
- 对染色体的某个基因进行变异
- 变异方式
- 位点变异:某个/每个位点以一定概率变异
- 逆转变异:随机选两点,将两点间的基因逆序
- 插入变异:随机选一个基因插入随机的插入点间
- 互换变异:随机选两个基因进行简单互换
- 移动变异:将某个基因向左/右移动随机位数
2、Python实现(非线性函数最优化问题为例)
(1)定义适应度函数
import math
def func(x, y):
num = 6.452 * (x + 0.125 * y) * (math.cos(x) - math.cos(2 * y)) ** 2
den = math.sqrt(0.8 + (x - 4.2) ** 2 + 2 * (y - 7) ** 2)
return num / den + 3.226 * y
(2)初始化GeneticAlgorith类
class GeneticAlgorithm:
def __init__(self, function, M, gen, Pc=0.85, Pm=0.05):
"""
:param function: fitness function
:param M: population
:param gen: total generations
:param Pc: probability of crossover
:param Pm: probability of mutation
"""
self.func = function
self.Pc = Pc
self.Pm = Pm
self.M = M
self.gen = gen
self.dec_num = 3
self.X = []
self.Y = []
self.chr = []
self.f = []
self.rank = []
self.history = {
'f': [],
'x': [],
'y': []
}
(3)编码函数
定义编码方式:x, y => chromosome
- 例:x=3.124, y=5.637, 则chromosome=“31245637”
def num2str(self, num):
# return str(int(num)) + str(int(num - int(num)) * 1e3)
s = str(num).replace('.', '')
s += '0' * abs(int(num) // 10 + 1 + self.dec_num - len(s))
return s
def encoder(self, x, y):
chr_list = []
for i in range(len(x)):
chr = self.num2str(x[i]) + self.num2str(y[i])
chr_list.append(chr)
return chr_list
于此同时,定义编码方式所对应的解码方式:chromosome => x, y
def str2num(self, s):
num = int(s[:-self.dec_num]) + float(s[-self.dec_num:]) / 10 ** self.dec_num
return round(num, self.dec_num)
def decoder(self, chr):
cut = int(len(chr[0]) / 2)
x = [self.str2num(chr[i][:cut]) for i in range(len(chr))]
y = [self.str2num(chr[i][cut:]) for i in range(len(chr))]
return x, y
(4)选择后代染色体
这里以适应度比例作为选择方式,通过轮盘赌的方法随机选择M次,得到M个新后代(适应度比例越大,轮盘赌中随机数落在该扇区的概率就越大,被选中的概率就越高)
from random import random
def choose(self):
# calculate percentage
s = sum(self.f)
p = [self.f[i] / s for i in range(self.M)]
chosen = []
# choose M times
for i in range(self.M):
cum = 0
m = random()
# Roulette
for j in range(self.M):
cum += p[j]
if cum >= m:
chosen.append(self.chr[j])
break
return chosen
(5)交叉
使用一点交叉作为交叉算子,对每两条染色体以Pc的概率进行交叉
from random import randint
def crossover(self, chr):
crossed = []
# if chr list is odd
if len(chr) % 2:
crossed.append(chr.pop())
for i in range(0, len(chr), 2):
a = chr[i]
b = chr[i + 1]
# 0.85 probability of crossover
if random() < self.Pc:
loc = randint(1, len(chr[i]) - 1)
temp = a[loc:]
a = a[:loc] + b[loc:]
b = b[:loc] + temp
# add to crossed
crossed.append(a)
crossed.append(b)
return crossed
(6)变异
用位点变异的方法,对某条染色体的每一位基因以概率Pm进行变异,并确保变异后与变异前的基因不同
def mutation(self, chr):
res = []
for i in chr:
l = list(i)
for j in range(len(l)):
# 0.05 probability of mutation on each location
if random() < self.Pm:
while True:
r = str(randint(0, 9))
if r != l[j]:
l[j] = r
break
res.append(''.join(l))
return res
(7)主函数
先对染色体种群进行初始化并编码,然后开始迭代进化:
- 对每一代染色体计算相应的适应度值和排名,打印信息
- 保存到history,便于后续绘制折线图
- 进行染色体的选串复制、交叉与变异
- 对染色体解码,完成一次迭代
from random import uniform
def run(self):
# initialization
x = []
y = []
for i in range(self.M):
x.append(round(uniform(0, 10), self.dec_num))
y.append(round(uniform(0, 10), self.dec_num))
self.X = x
self.Y = y
self.chr = self.encoder(x, y)
# iteration
for iter in range(self.gen):
self.f = [func(self.X[i], self.Y[i]) for i in range(self.M)]
fitness_sort = sorted(enumerate(self.f), key=lambda x: x[1], reverse=True)
# 1st : fitness[rank[0]]
self.rank = [i[0] for i in fitness_sort]
winner = self.f[self.rank[0]]
print(f'Iter={iter + 1}, Max-Fitness={winner}')
# save to history
self.history['f'].append(winner)
self.history['x'].append(self.X[self.rank[0]])
self.history['y'].append(self.Y[self.rank[0]])
# choose, crossover and mutation
chosen = self.choose()
crossed = self.crossover(chosen)
self.chr = self.mutation(crossed)
self.X, self.Y = self.decoder(self.chr)
(8)运行结果
实例化GeneticAlgorith类,设置种群数为10,迭代次数为100次
if __name__ == '__main__':
# run
ga = GeneticAlgorithm(func, 10, 100)
ga.run()
# plot
plt.plot(ga.history['f'])
plt.title('Fitness value')
plt.xlabel('Iter')
plt.show()
运行得到结果如下
每一次遗传算法的运算结果都可能有较大的不同,这跟初始种群的选取、交叉等操作有密切的联系,如果想提高稳定性可以进行参数的调整,如扩大种群的数量,增加迭代次数,选用不同的交叉、变异方法和相应的概率,以优化这一模型,得到更加理想的结果。
以上是遗传算法的Python实现,最后附上完整代码:
# -*- coding: utf-8 -*-
# @Author : gyy
# @Email : [email protected]
# @File : GA.py
import math
import matplotlib.pyplot as plt
from random import random, randint, uniform
def func(x, y):
num = 6.452 * (x + 0.125 * y) * (math.cos(x) - math.cos(2 * y)) ** 2
den = math.sqrt(0.8 + (x - 4.2) ** 2 + 2 * (y - 7) ** 2)
return num / den + 3.226 * y
class GeneticAlgorithm:
def __init__(self, function, M, gen, Pc=0.85, Pm=0.05):
"""
:param function: fitness function
:param M: population
:param gen: total generations
:param Pc: probability of crossover
:param Pm: probability of mutation
"""
self.func = function
self.Pc = Pc
self.Pm = Pm
self.M = M
self.gen = gen
self.dec_num = 3
self.X = []
self.Y = []
self.chr = []
self.f = []
self.rank = []
self.history = {
'f': [],
'x': [],
'y': []
}
def num2str(self, num):
# return str(int(num)) + str(int(num - int(num)) * 1e3)
s = str(num).replace('.', '')
s += '0' * abs(int(num) // 10 + 1 + self.dec_num - len(s))
return s
def encoder(self, x, y):
chr_list = []
for i in range(len(x)):
chr = self.num2str(x[i]) + self.num2str(y[i])
chr_list.append(chr)
return chr_list
def str2num(self, s):
num = int(s[:-self.dec_num]) + float(s[-self.dec_num:]) / 10 ** self.dec_num
return round(num, self.dec_num)
def decoder(self, chr):
cut = int(len(chr[0]) / 2)
x = [self.str2num(chr[i][:cut]) for i in range(len(chr))]
y = [self.str2num(chr[i][cut:]) for i in range(len(chr))]
return x, y
def choose(self):
# calculate percentage
s = sum(self.f)
p = [self.f[i] / s for i in range(self.M)]
chosen = []
# choose M times
for i in range(self.M):
cum = 0
m = random()
# Roulette
for j in range(self.M):
cum += p[j]
if cum >= m:
chosen.append(self.chr[j])
break
return chosen
def crossover(self, chr):
crossed = []
# if chr list is odd
if len(chr) % 2:
crossed.append(chr.pop())
for i in range(0, len(chr), 2):
a = chr[i]
b = chr[i + 1]
# 0.85 probability of crossover
if random() < self.Pc:
loc = randint(1, len(chr[i]) - 1)
temp = a[loc:]
a = a[:loc] + b[loc:]
b = b[:loc] + temp
# add to crossed
crossed.append(a)
crossed.append(b)
return crossed
def mutation(self, chr):
res = []
for i in chr:
l = list(i)
for j in range(len(l)):
# 0.05 probability of mutation on each location
if random() < self.Pm:
while True:
r = str(randint(0, 9))
if r != l[j]:
l[j] = r
break
res.append(''.join(l))
return res
def run(self):
# initialization
x = []
y = []
for i in range(self.M):
x.append(round(uniform(0, 10), self.dec_num))
y.append(round(uniform(0, 10), self.dec_num))
self.X = x
self.Y = y
self.chr = self.encoder(x, y)
# iteration
for iter in range(self.gen):
self.f = [func(self.X[i], self.Y[i]) for i in range(self.M)]
fitness_sort = sorted(enumerate(self.f), key=lambda x: x[1], reverse=True)
# 1st : fitness[rank[0]]
self.rank = [i[0] for i in fitness_sort]
winner = self.f[self.rank[0]]
print(f'Iter={iter + 1}, Max-Fitness={winner}')
# save to history
self.history['f'].append(winner)
self.history['x'].append(self.X[self.rank[0]])
self.history['y'].append(self.Y[self.rank[0]])
# choose, crossover and mutation
chosen = self.choose()
crossed = self.crossover(chosen)
self.chr = self.mutation(crossed)
self.X, self.Y = self.decoder(self.chr)
if __name__ == '__main__':
# run
ga = GeneticAlgorithm(func, 10, 100)
ga.run()
# plot
plt.plot(ga.history['f'])
plt.title('Fitness value')
plt.xlabel('Iter')
plt.show()