【IHS+稀疏表示】基于IHS小波变换和稀疏表示相结合的遥感图像融合算法matlab仿真

1.软件版本

matlab2013b

2.本算法理论知识

       小波变换具有多尺度特性，其时域和频域均 具有表征信号局部特性的能力和多分辨率分析的 特点。在低频时具有高的频谱分辨率，在高频 时具有低的频谱分辨率，因而能有效地从信号中 提取信息。通过小波变换可将图像分解为一个低 频分量和一系列的高频分量，其中低频分量为近 似图像，高频分量为图像的细节信息，如边缘、亮 线、区域边界等。 Hu 等人［4］提出基于稀疏表示和 IHS 变换的遥 感图像融合，基本思路是对多光谱图像进行 IHS 变 换后对 I 分量和全色图像进行稀疏表示，之后用绝 对值取大的融合规则对其稀疏系数进行融合，重构 I 分量，最后进行 IHS 逆变换，得到融合图像。 由于 IHS 变换具有严重的光谱失真，考虑将小 波变换与 IHS 变换相结合。如图 1 算法流程所示， 首先对多光谱图像进行 IHS 变换，得到对应的 I、H、 S 分量，对与光谱特性不相关的 I 分量进行 SFIM 运 算，将空间细节信息加入到 I 分量中，这样能尽可能 少地影响光谱信息，并通过 SFIM 模型将空间细节 信息合理、有效地调制到多光谱图像亮度分量中。 然后对运算后的 I 分量和全色图像进行小波变换， 得到对应的低频和高频系数，分别对高频和低频系 数进行融合，最后进行小波逆变换和 IHS 变换得到 融合图像。

3.部分源码

close all;
clear all;
clc

rng(1);

I4 = imread('PAN.jpg');%读取并显示图像
I2 = imread('MS.jpg'); 
%figure;subplot(2,3,1);imshow(I4);title('the origin image 1');subplot(2,3,2);imshow(I2);title('the origin image 2');
step=1; 
Dsize=256; u2=zeros(3,1);v12=zeros(3,1);
AA=[1/sqrt(3),1/sqrt(3),1/sqrt(3);       
    1/sqrt(6),1/sqrt(6),-2/sqrt(6);                   
    1/sqrt(2),-1/sqrt(2),0];
BB=[1/sqrt(3),1/sqrt(6),1/sqrt(2);
    1/sqrt(3),1/sqrt(6),-1/sqrt(2);                    
    1/sqrt(3),-2/sqrt(6),0];
I1=(I4);
 [I3,v1,v2]=ihs(I2,AA);%ihs变换    
 
 
[V1t_block] = getblock_new(I3, 3000,8,8,'random',1); %随机分块
[V2t_block] = getblock_new(I1, 3000,8,8,'random',1);
V_train = [V1t_block,V2t_block];
D0 = Initial_Dictionary(64,Dsize); 
%load('D.mat');%load('V_train.mat');
D = train_Dictionary_new( V_train ,D0,'OMP', 'K-SVD',0.01);% 训练字典 
clear V1t_block V2t_block V_train;
[V1_block] = getblock_new(I3, 1000,8,8,'sliding',step);  %分块并用omp求稀疏系数
[l, m] = size(V1_block);
[h,w] = size(D);
a1 = zeros(w,m);
for i = 1:m
    a1(:,i) = solveRepresentation(100,D, V1_block(:,i),'denoise', 0.001, 'OMP');  
end
clear V1_block;

[V2_block] = getblock_new(I1, 1000,8,8,'sliding',step); 
[l, m] = size(V2_block);
a2 = zeros(w,m);
for i = 1:m
    a2(:,i) = solveRepresentation(100,D, V2_block(:,i),'denoise', 0.001, 'OMP');  
end
clear V2_block;



a_f = fusion_criterion(a1,a2,'max');
X_f= D*a_f; 
[height,width]=size(I1);
img_f = showImage_new(X_f,height,width,'sliding',step);
%
RGB=ihs1(I1,img_f,BB,v1,v2);%逆变换
%subplot(2,3,3);figure;%重构并显示图像
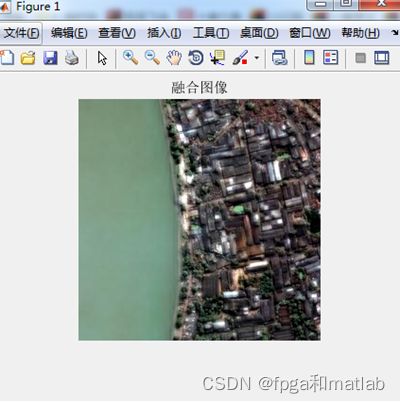
imshow(RGB);
title('融合图像');

%信息熵
entropy = func_entropy(RGB(:,:,3));
entropy
%边缘强度
outval = edge_intensity(RGB(:,:,3)); 
outval
%平均梯度
outval = avg_gradient(RGB(:,:,3));  
outval

4.仿真结论

	信息熵	边缘强度	平均梯度
1原稀疏表示IHS	7.1354	94.8276	9.3842
2IHS改进	6.3183	76.2175	7.8215
3 IHS改进的基础上进行修改完善	7.0371	96.4255	9.4937

1

2

 

 3

 A28-53