梯度,GD梯度下降,SGD随机梯度下降
前言
羊了,但是依旧生龙活虎。补补之前落下的SGD算法,这个在深度学习中应用广泛。
梯度(Gradient)
方向导数
在梯度之前,非常重要一个概念:方向导数,这里 u u u是 n n n维向量,代表一个方向,通过极限的方式定义函数 f f f在方向 u u u上的导数,或者说增长率:

当 u u u是标准(正交)单位向量 i i i时(坐标轴方向),方向导数退化为偏导数: ∇ u f ( x ) = f i ′ ( x ) = ∂ f ( x ) ∂ x i \nabla_uf(x)=f_i'(x)=\frac{\partial f(x)}{\partial x_i} ∇uf(x)=fi′(x)=∂xi∂f(x)
任意一个方向导数可以用单位向量的线性组合表示:

证明:

这是一个构造性证明,而且由于 f i ′ ( x ) f_i'(x) fi′(x)之间线性无关, u i u_i ui应是唯一的。中间用到的高维链式求导法则,其实一定程度上隐含了这种分解性,换而言之,利用偏导的分解性推导出更为一般的方向导数的分解性质。
梯度定义

梯度就是函数对所有单位向量求偏导构成的向量(方向),代表函数 f f f在定义空间 R n R^n Rn中的“增长率”。利用方向导数的定义,以及前面的定理,得 ∇ u f ( x ) = ∇ f ( x ) ⋅ u = ∣ ∣ ∇ f ( x ) ∣ ∣ ∣ u ∣ ∣ c o s α \nabla_uf(x)=\nabla f(x)\cdot u=||\nabla f(x)|||u||cos\alpha ∇uf(x)=∇f(x)⋅u=∣∣∇f(x)∣∣∣u∣∣cosα
α \alpha α是 ∇ u f ( x ) \nabla_uf(x) ∇uf(x)和 u u u的夹角。
不妨设 u u u是单位向量,化简得到方向导数和梯度之间的关系:
∇ u f ( x ) = ∣ ∣ ∇ f ( x ) ∣ ∣ c o s α \nabla_uf(x)=||\nabla f(x)||cos\alpha ∇uf(x)=∣∣∇f(x)∣∣cosα
当 u = ∇ f ( x ) u=\nabla f(x) u=∇f(x)时, α = 0 \alpha=0 α=0,得到了最大的方向导数,这意味着,梯度是函数变化最剧烈的方向,是定义在空间 R n R^n Rn中的“增长率”。
梯度下降算法(Gradient Desent Algorithm)
算法思想
如果多元函数 J ( θ ) J(\theta) J(θ)在点 θ \theta θ的邻域内可微,则 θ \theta θ向梯度反方向变化, J ( θ ) J(\theta) J(θ)下降得最快。可以通过梯度下降找到函数的局部最小点。

这里, θ \theta θ通常随机初始化, α \alpha α是学习率。通常的收敛准则为梯度大小小于预定义阈值(这通常意味着已经收敛到一个较平缓的的区域——极值点处)或者达到设置的最大迭代轮数。
如何计算梯度?
其实,和算偏导一样,只不过逐一对每个变量效率太低了,因而归纳一类变量的特征,进行求导,也就是向量求导、矩阵求导。
eg.线性回归函数:
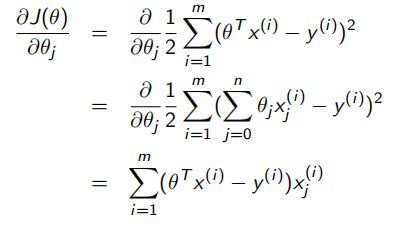
学习率
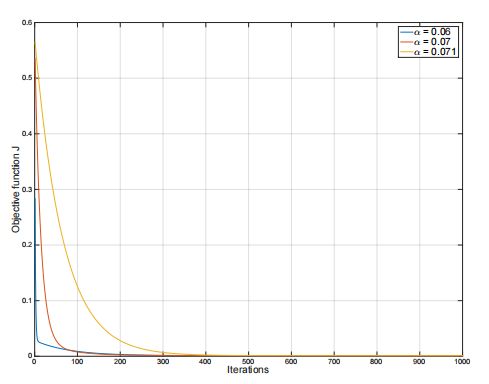
每次迭代朝梯度反方向的移动步长。
学习率越大,收敛越快,但过大会导致无法收敛,可能达到目标只需要一小步,迈大步怎么也无法到达目标;
学习率过小,收敛速度过大,影响模型效率;
因此调一个合适的学习率参数很必要。
随机梯度下降算法(Stochastic Gradient Descent)
GD在训练集过于庞大时,会产生巨大的计算成本!
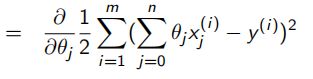
如较为简单的线性回归,梯度计算量和训练集大小 m m m是线性关系。巨额的计算只为移动一小步,这似乎是很不划算的,因此有了随机梯度下降。SGD中参数仅依据一个训练样本进行更新,而不是整个数据集!更新 m m m次!而随机,是指更新选择的样本顺序在每轮迭代中是随机生成。

SGD在深度学习中的应用
SGD在神经网络中担任优化器的角色,The Optimizer,实际上几乎所有深度学习的优化算法属于SGD一族,遵循以下运作模式:

batch & epoch
每轮迭代使用的训练样本称为一个批处理,batch;完整使用一遍训练集称为一个epoch,通常epoch大小代表一个sample会进入网络的次数。
learning rate & batch size
SGD的两个重要参数,它们之间的相互作用是微妙的。但实际上多数情况下,我们不需要调参。Adam是一种具有自适应学习率的SGD算法,无需任何参数调优,可以“自调优”。
以上是在Kaggle平台的深度学习入门课程的第三讲部分内容(Stochastic Gradient Descent),并为深入进行讨论,下面是基于Keras的简单神经网络实现以及训练:
构建网络:
from tensorflow import keras
from tensorflow.keras import layers
model = keras.Sequential([
layers.Dense(512, activation='relu', input_shape=[11]),
layers.Dense(512, activation='relu'),
layers.Dense(512, activation='relu'),
layers.Dense(1),
])
设置Optimizer和loss function:
model.compile(
optimizer='adam',
loss='mae',
)
训练:
history = model.fit(
X_train, y_train,
validation_data=(X_valid, y_valid),
batch_size=256,
epochs=10,
)
