寒假博客日记——第一天
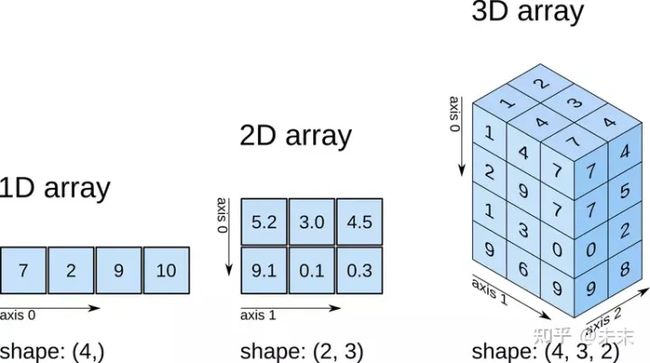
Python中axis的意思
对于一个多维张量,如a=[4,3,6]存在3个轴,从左至右依次底层,分别为axis=0,axis=1,axis=2。
axis的选择在自定义损失函数中会经常用到,要注意理解。
下面边理解axis边练习张量的书写:
a1=np.array([[1,2,3],[4,5,6]]).astype(np.float64)
a2=np.array([[1,1,1],[3,3,3]]).astype(np.float64)
将a1-a2求平方:
tf.square(a1-a2)
<tf.Tensor: shape=(2, 3), dtype=float64, numpy=
array([[0., 1., 4.],
[1., 4., 9.]])>
此时得到的是一个[2,3]维度的张量,对其两个轴分别求平均:
tf.reduce_mean(tf.square(a1-a2),axis=0)
<tf.Tensor: shape=(3,), dtype=float64, numpy=array([0.5, 2.5, 6.5])>
对axis=0求平均,方向是纵向的:↓。可以直观的想象有一根叉子,像串糖葫芦一样,从上到下把所有的数串在一起,由于执行的是求平均数的操作,所以这些被串在一起的数被执行了求平均数。
axis=1时类似:
tf.reduce_mean(tf.square(a1-a2),axis=1)
<tf.Tensor: shape=(2,), dtype=float64, numpy=array([1.66666667, 4.66666667])>
各axis的直观理解:
关于tf相关的张量运算在之后的练习中要反复加强,目前还理解得很肤浅。
自定义损失函数(参数只包含y_true和y_pred)的写法
任何具有y_true和y_pred两个参数,并且返回一个和输入批次相同大小的数组的函数都可以作为损失函数,通过实例化损失类来创建。
例如y_true和y_pred是一个批大小为32,维度为10的张量,即其尺寸为[32,10],那么损失函数返回的值应当是一个[32]大小的张量
自定义mse损失函数:
def my_loss(y_true,y_pred):
y_true=tf.cast(y_true,dtype=tf.float32)
y_pred=tf.cast(y_pred,dtype=tf.float32)
loss=tf.reduce_mean((y_true-y_pred)**2,axis=1)
return loss
测试一下结果:
my_loss(a1,a2)
<tf.Tensor: shape=(2,), dtype=float32, numpy=array([1.6666666, 4.6666665], dtype=float32)>
tf.losses.mse(a1,a2)
<tf.Tensor: shape=(2,), dtype=float64, numpy=array([1.66666667, 4.66666667])>
除了精度不同外,其他方面一致。
一个有问题的交叉熵函数:
def my_loss(y_true,y_pred):
y_true=tf.cast(y_true,dtype=tf.float32)
y_pred=tf.cast(y_pred,dtype=tf.float32)
loss=-kb.sum(y_true*kb.log(y_pred)+(1-y_true)*kb.log(1-y_pred))
return loss
由于没有处理log0=-inf这类问题,所以我定义的这个交叉熵函数是有问题的,在计算的过程中出现nan,导致不能训练模型
今天遇到的问题以及解决办法:
- 编写的损失函数出现类型不匹配
TypeError: Input ‘y‘ of ‘Sub‘ Op has type int32 that does not match type float32 of argument ‘x‘.
解决办法:使用tf.cast函数做数据类型转换。
y_true=tf.cast(y_true,dtype=tf.float32)
y_pred=tf.cast(y_pred,dtype=tf.float32)
整数通常是不适合用来做张量运算的,如果读入的图片如果是int8类型的,一般在要在训练前把图像的数据格式转换为float32。
而我遇到的问题是y_pred - y_true的数据类型不同,y_pred的类型是float32,而y_true的类型是int32。
- 自定义交叉熵损失函数计算出现nan值
由于0*log0=nan,log0=-inf,所以在计算交叉熵时很容易出现nan值,我编写的交叉熵函数就在训练中出现了nan,导致模型无法正常训练:
loss=-kb.sum(y_true*kb.log(y_pred)+(1-y_true)*kb.log(1-y_pred))
在https://blog.csdn.net/qq_36201400/article/details/112302584中有详细的解决过程。主要分为三个方法:
- 方法1. 给a加上一个极小值
- 方法2. 当a接近0时, 给a一个极小值
- 方法3. 出现nan时, 设置损失为0
总之,不能让损失函数计算出现nan值。
在tf的二元交叉熵中也是类似做的,y_true=[0]和y_pred[1]的二元交叉熵为15.33多,而不是无穷大,具体如下:
tf.losses.binary_crossentropy([0.0],[1.0])
<tf.Tensor: shape=(), dtype=float32, numpy=15.333239>
如果y_true和y_pred均为0,那么按理说损失函数也要为0,而非nan:
tf.losses.binary_crossentropy([0.0],[0.0])
<tf.Tensor: shape=(), dtype=float32, numpy=-0.0>
一些题外话:
当y_true为0而预测值y_pred为1时,交叉熵有15.33,而如果将y_pred设置为0.95,交叉熵减小到2.996,这在进行一些竞赛时能够很大的减少分类错误造成的惩罚。属于一个小技巧。
让预测值最大为0.95,最小为0.05。假设分类错误,能够极大减小惩罚:
tf.losses.binary_crossentropy([0.0],[1.0])
<tf.Tensor: shape=(), dtype=float32, numpy=15.333239>
tf.losses.binary_crossentropy([0.0],[0.95])
<tf.Tensor: shape=(), dtype=float32, numpy=2.99573>
假设分类正确,造成的额外代价很小:
tf.losses.binary_crossentropy([0.0],[0.0])
<tf.Tensor: shape=(), dtype=float32, numpy=-0.0>
tf.losses.binary_crossentropy([0.0],[0.05])
<tf.Tensor: shape=(), dtype=float32, numpy=0.051293183>
这也就是我们常说的话不要说得太满,不然打脸的时候会很疼。不要说有100%的把握xxx。说有95%的把握就好了。
总结
今天学的东西很少,不过俗话说万事开头难,有了一个开头,之后坚持下去的难度会小很多。阳了已经一周多了,没有明显的难受症状了,但是有点嗜睡,每天都要睡十一二个小时,导致能够自由支配的时间大大减少了,希望尽快恢复吧。
接下来想学一下多参数的损失函数,能够将网络中隐藏层的输出也写到损失函数里面,这都是在为自洽正则化在做铺垫,在掌握损失函数的自定义之后,会尝试复现一些论文。