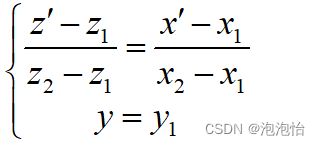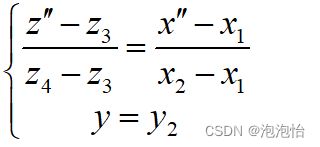双线性插值公式推导及Matlab实现
一、引言
双线性插值作为一种比较简单的二维插值方法,常用于曲面插值或者图像插值。双线性插值需要已知四个角点坐标(xi,yi,zi),i=1,2,3,4,然后以此构建一张曲面片,即插值曲面。根据这四个已知角点,利用双线性插值函数,就可以计算该插值曲面片内部各点处的函数值,也可以用来预测该插值曲面片外部邻近区域的函数值。
二、双线性插值公式推导
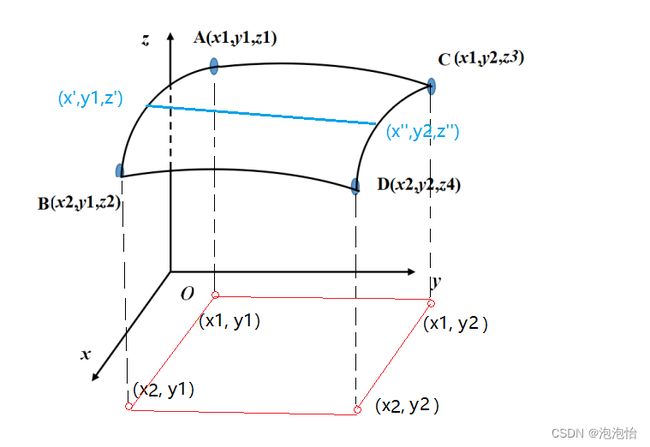
如下图所示曲面片,四个角点坐标已知,对应的xoy平面矩形区域。
1)根据点A和点B建立直线AB方程,坐标是(x’,y1,z’):
2)根据点C和点D建立直线CD方程,坐标是(x’’,y2,z’’):
3)以直线AB和直线CD为端点,建立同时垂直于AB与CD的直线:
4)将式(1)和式(2)代入式(3)得:
该函数就是双线性插值函数。(虽然该公式看着稍微有点烦,但是你不能不说它很简单)
当四个角点分别是图像相邻的四个角点时,且假设其中一个角点(x1,y1)位于原点,由于相邻的像素距离是1,所以上式中的分母都是1,则可以得到图像上相邻四个像素构成的曲面片的插值函数为:
此公式即为图像的双线性插值公式。(图像的双线性插值原来如此简单)
二、曲面片的双线性插值实例(纯纯的手工,非interp1)
例1. 已知某曲面的四个角点坐标分别为( 0.1, 0.1 ), ( 0.1, 1.2 ), ( 1.1, 0.1 ), ( 1.1, 1.2 ),利用双线性插值完成该曲面插值,绘制插值插值之后的曲面片。
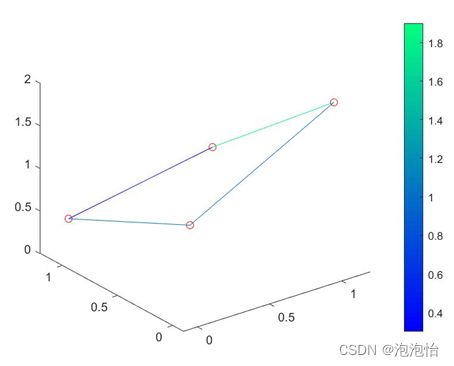
1)绘制四个角点构成曲面网格图:
参考代码:
clear all
clc
x = [ 0.1, 0.1; 1.1, 1.1 ];
y = [ 0.1, 1.2; 0.1, 1.2 ];
z = [ 1, 0.3; 1.9, 0.6 ];
plot3( x, y, z, 'ro' )
hold on
mesh( x, y, z )
colormap winter
colorbar
axis( [ -0.1, 1.2, -0.1, 1.2, 0, 2 ] )
hidden off
运行结果如下:
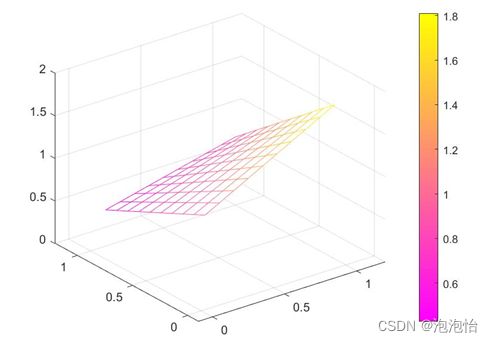
2)绘制利用曲面片内部插值点生成的网格曲面片
[ xi, yi ] = meshgrid( [ 0.1 : 0.1 : 1 ] );
x1 = x(1, 1);
x2 = x(2, 1);
y1 = y(1, 1);
y2 = y(1, 2);
z1 = z(1, 1);
z2 = z(2, 1);
z3 = z(1, 2);
z4 = z(2, 2);
x2_1 = x2 - x1;
y2_1 = y2 - y1;
yi_1 = yi - y1;
xi_1 = xi - x1;
zi = ( yi_1 .* xi_1 * ( z1 - z2 - z3 + z4 ) ) / ( x2_1 .* y2_1 ) ...
+ ( yi_1 .* ( z3 - z1 ) ) / y2_1 + ( xi_1 .* ( z2 - z1 ) ) / x2_1 + z1;
mesh( xi , yi, zi )
colormap spring
axis( [ -0.1, 1.2, -0.1, 1.2, 0, 2 ] )
colorbar
运行结果:
3)增加外部插值点之后得到的插值曲面
参考代码:(只需要修改横坐标和纵坐标取值范围即可)
[ xi, yi ] = meshgrid( [ -0.5 : 0.1 : 1.5 ] );
x1 = x(1, 1);
x2 = x(2, 1);
y1 = y(1, 1);
y2 = y(1, 2);
z1 = z(1, 1);
z2 = z(2, 1);
z3 = z(1, 2);
z4 = z(2, 2);
x2_1 = x2 - x1;
y2_1 = y2 - y1;
yi_1 = yi - y1;
xi_1 = xi - x1;zi = ( yi_1 .* xi_1 * ( z1 - z2 - z3 + z4 ) ) / ( x2_1 .* y2_1 ) ...
+ ( yi_1 .* ( z3 - z1 ) ) / y2_1 + ( xi_1 .* ( z2 - z1 ) ) / x2_1 + z1;
mesh( xi , yi, zi )
colormap spring
axis( [ -0.5, 1.6, -0.5, 1.6, -1, 3 ] )
colorbar
运行结果: