图像插值算法：最近邻插值、双线性插值

插值算法：最近邻插值、双线性插值

插值算法有很多种，这里列出关联比较密切的三种：
最近邻法(Nearest Interpolation)：计算速度最快，但是效果最差。

双线性插值(Bilinear Interpolation)：双线性插值是用原图像中4(2*2)个点计算新图像中1个点，效果略逊于双三次插值，速度比双三次插值快，属于一种平衡美，在很多框架中属于默认算法。

双三次插值(Bicubic interpolation)：双三次插值是用原图像中16(4*4)个点计算新图像中1个点，效果比较好，但是计算代价过大。

最近邻插值法（nearest_neighbor)

1.原理与应用

最近邻插值法nearest_neighbor是最简单的灰度值插值。也称作零阶插值，就是令变换后像素的灰度值等于距它最近的输入像素的灰度值。最近邻插值法可应用于图像的缩放，因为简单的变换与计算，效果一般不好。举例说明其变换过程：

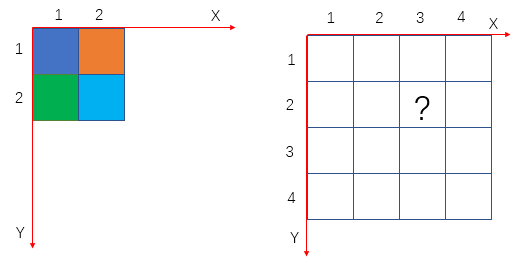
先假设一个2X2像素的图片采用最近邻插值法需要放大到4X4像素的图片，右边？该为多少。

2. 公式及计算

最近邻插值法坐标变换计算公式：

srcX=dstX*(srcWidth/dstWidth)

srcY=dstY*(srcHeight/dstHeight)

上式中，dstX与dstY为目标(destination)图像的某个像素的横纵坐标，dstWidth与dstHeight为目标图像的长与宽；srcWidth与srcHeight为原(source)图像的宽度与高度。srcX，srcY为目标图像在该点（dstX，dstY）对应的原图像的坐标。至于公式为啥是这个样，和容易理解，如果是放大图像，(srcWidth/dstWidth)值小于1，同样将dstX同比例映射到原图像的srcX中，如果srcWidth/dstWidth=1，就相当于复制了图片。

图像坐标以左上角为(0,0)坐标。

右图为经过放大后的目标图像，**？**处的坐标为(3,2)，根据公式计算得到

srcX=3*(2/4)=1.5，srcY=2*(2/4)=1；故？处的像素应该为原图像中的(1.5,1)像素的值，但是像素坐标没有小数，一般采用四舍五入取最邻，所以最终的结果为(2,1)，对应原图像的橙色。其他类比得到放大后的图像：

线性插值

说双线性之前先说一下单线性，因为在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。

双线性插值是上采样的一种。在上采样过程中，要恢复图片的大小，提高图片的分辨率，就要用到一些方法，任何可以让图片变成高分辨率的技术都可以称为上采样。

单线性插值法

线性插值法，是指使用连接两个已知量的直线来确定在这两个已知量之间的一个未知量的值的方法。

根据初中的知识，2点求一条直线公式(这是双线性插值所需要的唯一的基础公式)

经过简单整理成下面的格式：

这里没有写成经典的AX+B的形式，因为这种形式从权重的角度更好理解。

首先看分子，分子可以看成x与x1和x2的距离作为权重，这也是很好理解的，P点与P1、P2点符合线性变化关系，所以P离P1近就更接近P1，反之则更接近P2。

现在再把公式中的分式看成一个整体，原式可以理解成y1与y2是加权系数，如何理解这个加权，要返回来思考一下，咱们先要明确一下根本的目的：咱们现在不是在求一个公式，而是在图像中根据2个点的像素值求未知点的像素值。这样一个公式是不满足咱们写代码的要求的。

现在根据实际的目的理解，就很好理解这个加权了，y1与y2分别代表原图像中的像素值（x与x1和x2的距离作为权重），上面的公式可以写成如下形式：

双线性插值

根据定义和名字，可以看出就是两个方向的线性插值

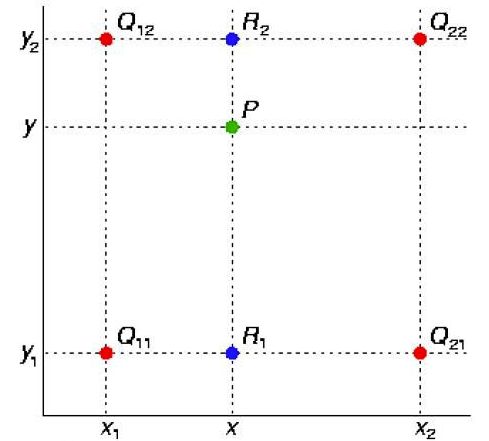
假如我们想得到未知函数f在点P= (x,y) 的值，假设我们已知函数f在Q11 = (x1,y1)、Q12 = (x1,y2),Q21 = (x2,y1) 以及Q22 = (x2,y2) 四个点的值。

首先在x方向进行线性插值，得到R1和R2，

然后在y方向进行线性插值，得到P.

整合后的公式如下

2. 图像计算例子

在图像处理的时候，我们先根据

srcX=dstX*(srcWidth/dstWidth)

srcY=dstY*(srcHeight/dstHeight)

来计算目标像素在源图像中的位置（和最近邻插值法一样，但是线性插值的像素是通过公式计算的），这里计算的srcX和srcY一般都是浮点数，

设坐标通过反向变换得到的浮点坐标为 (i+u,j+v) (其中i、j均为浮点坐标的整数部分，u、v为浮点坐标的小数部分，是取值[0,1)区间的浮点数)，则这个像素得值 f(i+u,j+v) 可由原图像中坐标所对应的周围四个像素的值决定，

计算公式由上面整合后的公式替换得到：

f(i+u,j+v) = (1-u)(1-v) f(i,j) + (1-u)v f(i,j+1) + u(1-v) f(i+1,j) + uv f(i+1,j+1)

注：

matlab、openCV对应的resize（）函数的源坐标和目标坐标转换和一般的不一样。

是

SrcX=(dstX+0.5)* (srcWidth/dstWidth) -0.5

SrcY=(dstY+0.5) * (srcHeight/dstHeight)-0.5

python代码

# coding=utf-8
import cv2
import numpy as np
import time

def resize(src, new_size):
    dst_w, dst_h = new_size # 目标图像宽高
    src_h, src_w = src.shape[:2] # 源图像宽高
    if src_h == dst_h and src_w == dst_w:
        return src.copy()
    scale_x = float(src_w) / dst_w # x缩放比例
    scale_y = float(src_h) / dst_h # y缩放比例

    # 遍历目标图像，插值
    dst = np.zeros((dst_h, dst_w, 3), dtype=np.uint8)
    for n in range(3): # 对channel循环
        for dst_y in range(dst_h): # 对height循环
            for dst_x in range(dst_w): # 对width循环
                # 目标在源上的坐标（浮点值）
                src_x = (dst_x + 0.5) * scale_x - 0.5
                src_y = (dst_y + 0.5) * scale_y - 0.5
                # 计算在源图上的（i,j）,和（i+1,j+1）的值
                src_x_0 = int(np.floor(src_x))  # floor是下取整
                src_y_0 = int(np.floor(src_y))
                src_x_1 = min(src_x_0 + 1, src_w - 1)
                src_y_1 = min(src_y_0 + 1, src_h - 1)

                # 双线性插值
                value0 = (src_x_1 - src_x) * src[src_y_0, src_x_0, n] + (src_x - src_x_0) * src[src_y_0, src_x_1, n]
                value1 = (src_x_1 - src_x) * src[src_y_1, src_x_0, n] + (src_x - src_x_0) * src[src_y_1, src_x_1, n]
                dst[dst_y, dst_x, n] = int((src_y_1 - src_y) * value0 + (src_y - src_y_0) * value1)
    return dst

if __name__ == '__main__':
    img_in = cv2.imread('test.jpg')
    start = time.time()
    img_out = cv2.resize(img_in, (600,600))
    print('cost %f seconds' % (time.time() - start))

    cv2.imshow('src_image', img_in)
    cv2.imshow('dst_image', img_out)
    cv2.waitKey()