策略梯度(Policy Gradient)算法学习
前面介绍的是Value-based 算法,每次都需要评估动作或者状态的价值。还有一种算法是直接学习参数化策略的方法。这个策略就是马尔科夫过程所讲的,给定一个状态s,智能体会采取什么样的动作,即 π ( s , a ) \pi(s,a) π(s,a)。这个概率分布,也就是我们的学习目标。
假设策略的待学习参数为 θ \theta θ,则在 t t t时刻、状态 s s s和参数 θ \theta θ下选择动作 a a a的概率为 π ( a ∣ s , θ ) = P r { A t = a ∣ S t = s t , θ t = θ } \pi(a|s,\theta)=Pr\{A_{t}=a|S_{t}=s_{t},\theta_{t}=\theta\} π(a∣s,θ)=Pr{At=a∣St=st,θt=θ}。
一、算法原理
算法的目标就是找到一组参数 θ \theta θ来最大化性能指标(即奖励函数)。
1、性能指标or策略目标函数
性能指标 J θ J_{\theta} Jθ的选择依赖于不同的问题类型,主要有以下三类:
- 在回合性(episodic)的环境中,我们用起始值(Start Value),也就是起始状态的价值:

- 在连续性环境中,不存在开始状态,可以使用平均值(Average Value)

- 在连续性环境中,或者用每一个时间步平均奖励(average reward per time-step)

2、策略优化
有了目标函数之后,我们采用梯度上升法(Gradient Ascent)来求解满足条件的参数 θ \theta θ。参数更新公式为:
θ t + 1 = θ t + α ▽ J ( θ t ) \theta_{t+1}=\theta_{t}+\alpha \bigtriangledown J(\theta_{t}) θt+1=θt+α▽J(θt)
3、策略梯度定理
我们以第一种策略目标函数为例进行分析,并采用离散动作空间。下面的推导过程来自李宏毅老师的讲解P4。
假设我们在策略 π θ \pi_{\theta} πθ下与环境交互,一直达到终止状态,并将智能体与环境交互过程中产生的state,action以及reward按顺序拼接起来,就是一条与环境交互的轨迹(trajectory)。
τ = { s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , … , s t , a t , r t } \tau = \left \{s_{1},a_{1},r_{1},s_{2},a_{2},r_{2},\dots ,s_{t},a_{t} ,r_{t} \right \} τ={s1,a1,r1,s2,a2,r2,…,st,at,rt}
如此一来,可以计算出这条轨迹发生的概率,如下图所示。
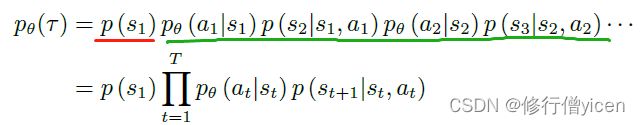
- 式中红色部分表示环境初始化时选择s1的概率。绿色部分的 p θ p_{\theta} pθ表示策略,即前面的 π θ \pi_{\theta} πθ; p ( s 2 ∣ s 1 , a 1 ) p(s_{2}|s_{1},a_{1}) p(s2∣s1,a1)表示在s1下执行动作a1,环境到达s2的概率,也就是状态转移概率。转移概率是由环境决定的,我们无法干预。智能体根据状态选择动作的策略则是可以学习得到的。
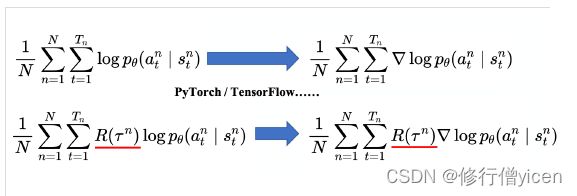
- 把轨迹 τ \tau τ中的奖励值加起来,就是该轨迹的总奖励 R ( τ ) R(\tau) R(τ)。
- 我们的目标是让奖励最大。但是 R ( τ ) R(\tau) R(τ)仅仅是众多可能的轨迹中的一条。因此我们将目标变为 R R R的期望最大。即

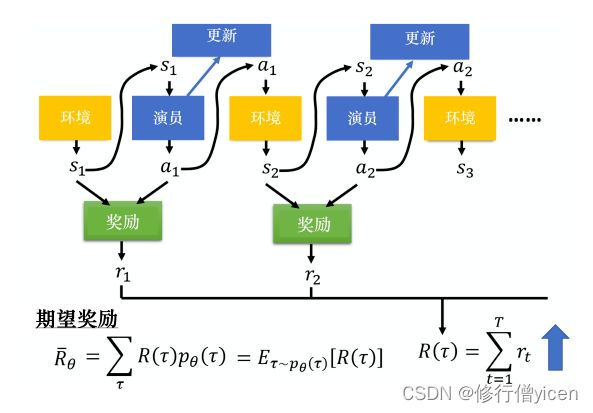
R ˉ θ \bar{R} _{\theta} Rˉθ对 θ \theta θ求导可得:
▽ R ˉ θ = ∑ τ R τ ▽ p θ ( τ ) \bigtriangledown \bar{R} _{\theta} =\sum_{\tau}R_{\tau}\bigtriangledown p_{\theta}(\tau) ▽Rˉθ=τ∑Rτ▽pθ(τ)
根据
▽ f ( x ) = f ( x ) ▽ l o g f ( x ) \bigtriangledown f(x)=f(x)\bigtriangledown logf(x) ▽f(x)=f(x)▽logf(x)
我们可以得到
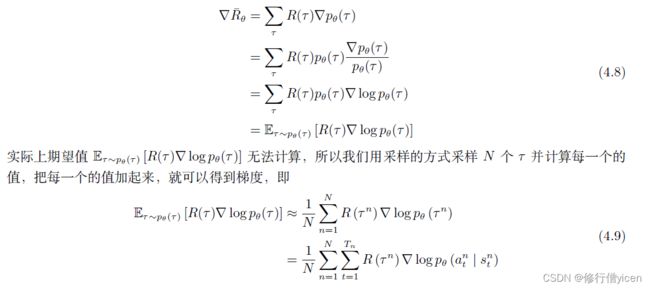
上式(4-9)中 ▽ l o g p θ ( τ ) \bigtriangledown logp_{\theta}(\tau) ▽logpθ(τ)的推导过程如下:
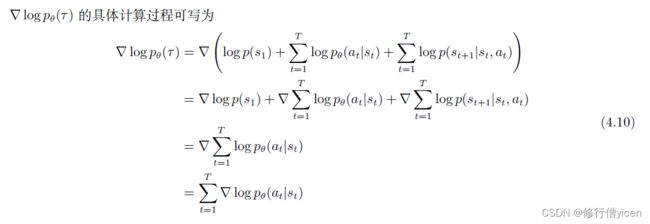
因此 ▽ R ˉ θ \bigtriangledown \bar{R} _{\theta} ▽Rˉθ可以表示为如下式:

最后策略梯度可以表示为:

- n表示第n条轨迹
- t表示第n条轨迹中的各个时刻
二、策略梯度的实现技巧
1、添加baseline
- 如果给定状态 s s s 采取动作 a a a,整场游戏得到正的奖励,就要增加
( s , a ) (s, a) (s,a) 的概率。如果给定状态 s s s 执行动作 a a a,整场游戏得到负的奖励,就要减小 ( s , a ) (s, a) (s,a)的概率。 - 但是在实际的场景中,有时候 R ( τ ) R(\tau) R(τ)总是正的,如果按照上面的策略梯度计算公式,那么不管什么动作,训练都是提高该动作的发生的概率,这显然是不合理。
- 因此,我们一般会对奖励做归一化。
- 但是,有些时候部分动作不会被采样到,如下图中的a。那么他的概率就不会提高,反而会下降。因此我们希望不同动作的奖励并不总是正的,希望他们有正有负。
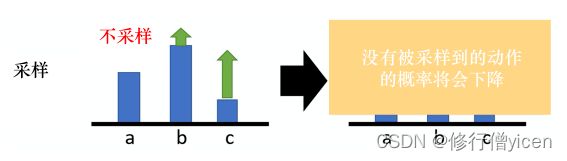
- 为了实现有正有负,我们可以让奖励值减去b。这样便可以得到有正有负的权重。
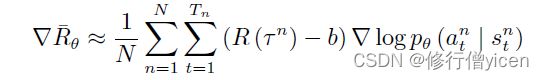
2、分配合适的权重
在前面的讲述中,对不同的状态-动作对概率梯度都用全局奖励值,都是用全局的奖励值作为它的权重进行更新。显然是不合理的。因为一个回合中,有些动作是好的,有些动作是坏的,但是最终的奖励不大,难道我们就放弃前面这个好动作的经验吗?
因此我们希望可以给每一个不同的动作前面都乘上不同的权重。每一个动作的不同权重反映了每一个动作到底是好的还是不好的。当前的状态执行的动作并不会对之前的状态产生影响。
所以我们计算某个状态-动作对的奖励的时候,不把整场游戏得到的奖励全部加起来,而是只计算从这个动作执行以后得到的奖励。只有从这个动作之后得到的奖励才能代表这个动作是否是坏。
此外,我们在计算奖励时,考虑 t t t时刻的动作对未来的影响大小,引入一个折扣因子 γ \gamma γ。因此,带有BaseLine的策略梯度公式就可以进一步表示为:

3. 优势函数
在实际的实现过程中, b b b是状态s的价值,上式中 ∑ t ′ = t T n γ t ′ − t r t ′ n \sum_{t^{'}=t}^{T_{n}} \gamma ^{t^{'}-t}r^{n}_{t^{'}} ∑t′=tTnγt′−trt′n表示从 t ′ t^{'} t′时刻开始,到游戏结束执行动作的奖励值,下文简称 R ( r t ′ ) R(r^{t^{'}}) R(rt′)。那么 R ( r t ′ ) − b R(r^{t^{'}})-b R(rt′)−b表示的就是在当前状态下执行该动作,相较于其他动作,到底有多好。这个优势函数可以表示为 A θ ( s t , a t ) A^{\theta}(s_{t},a_{t}) Aθ(st,at),一般由一个网络来估计,就是Critic。
三、策略梯度中概率的形式
- 对于离散动作:采用Softmax()
- 对于连续动作:一般表示为正态分布,均值和方差有参数化的函数近似给出。
四、策略梯度相关算法
- 蒙特卡洛策略梯度:REINFORCE
- 带baseline的REINFORCE
- Actor-Critic方法(代码待补充)
参考
- 第七讲 策略梯度(Policy Gradient)
- Datawhale的EasyRL