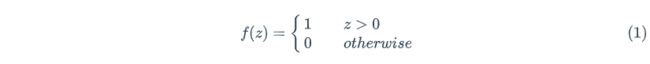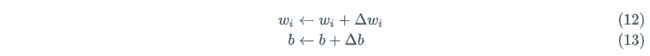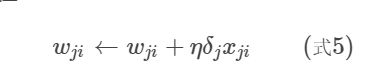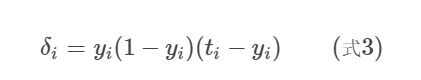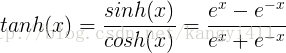深度学习基础算法梳理
1、实质用途
深度学习用来处理图像、语音等任务,也可用来处理数值型分类、回归任务。深度学习无需特征选择过程,具有较强的自学习能力,能拟合任意函数。
2、算法列表
2.1 感知器
感知器是由神经元,组成的一个基本的线性深度学习模型。用来解决线性分类问题。
感知器可实现基本的与、或函数、基本的二分类。它可以拟合任何的线性函数,任何线性分类或线性回归问题都可以用感知器来解决。
(1)感知器的定义
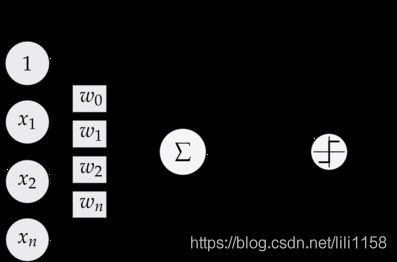
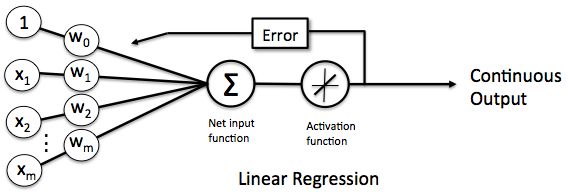
感知器为神经网络的组成单元,感知器的结构图片如下
感知器的公式如下:
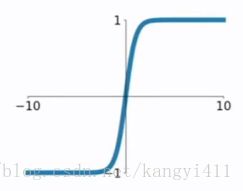
激活函数的公式如下:
感知器由输入权值、激活函数(阶跃函数)、输出组成。
(2)感知器的训练
权重更新的公式如下:
注意:此处t、y为一批输入的所有训练数据的y值。轮次则代表这个w更新几轮。如果轮次为1的话,此处w只更新一次。图中的学习率为每次更新的参数的跨度。
2.2 线性单元
感知器只能解决线性可分的情况,面对线性不可分的情况无法处理,线性单元就是为了解决线性不可分的情况。
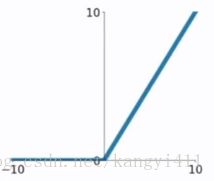
激活函数的公式为
f ( x ) = x f(x)=x f(x)=x
以上这种简单的激活函数,为线性回归,可以解决回归问题。
因此线性单元的公式为,其中X0为1,代表偏置b。目标函数为
y = w T x y=w^Tx y=wTx
e = 1 2 ( y − y ‾ ) 2 e=\frac{1}{2}(y−\overline{y})^2 e=21(y−y)2
2.3 全连接神经网络
在线性单元的基础上,激活函数变换为sigmoid等其他的激活函数,目标函数为均方差。因此参数更新公式如下
反向传播算法
代表从输出层往前一直求解权重的过程。
由于全连接神经网络参数太多,一般无法将参数传递超过3层。因此需要用其他网络来优化算法。
2.4 卷积神经网络
图像和语音识别一般选择卷积神经网络。激活函数一般选择relu为max(0,x)
relu速度快、减轻梯度小时、稀疏性
卷积神经网络由卷积层、池化层、全连接层组成。
卷积层:局部连接、权值共享【某一片节点连接1个输出,公用一个权值】提升计算效率可保留局部特征。(卷积相当于矩阵的内积,是对一片区域的特征提取过程,得到一个featuremap)
池化层:下采样【均值、最大值】
LeNet-5是实现手写数字识别的卷积神经网络,在MNIST测试集上,它取得了0.8%的错误率。
2.5 循环神经网络
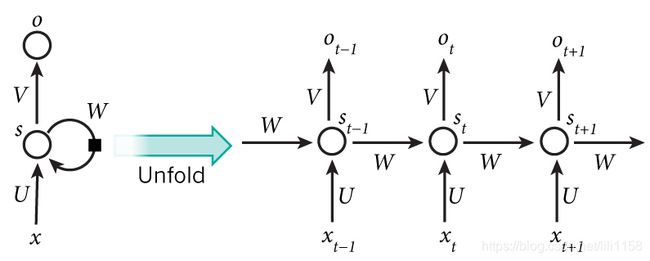
某些任务需要能够更好的处理序列的信息,即前面的输入和后面的输入是有关系的。同时输入的长度不是固定的。
网络结构如下,S值取决于当前的x值与上次隐藏层的s值。可以理解为当前来了个单次要看下一个单次是什么,不仅要拿当前单次,还要拿以前存储的信息库的信息。
循环神经网络为向前看,双向循环神经网络【结合向前看和向后看】
深度循环神经网络,代表中间有多个隐藏层
循环神经网络存在梯度爆炸和梯度消失问题,并不能真正的处理好长距离的依赖(虽然有一些技巧可以减轻这些问题)
2.6 长短时记忆神经网络
针对循环神经网络,增加一个来存储长期状态。包含输入门、遗忘门、新值门、输出门,其中原来RNN的状态不变,只是增加了一个C来存储长期状态。可以理解为上一个信息经过多重变换,保留信息的原始性,放在了h中。

3、基础概念
3.1目标函数
(1)0-1 loss函数
(2)交叉熵函数
(3)Hinge loss
(4)均方差损失
Hinge loss被用来解SVM问题中的间距最大化问题。
回归任务的损失
(5)L1损失(MAE)
(6)L2损失(MSE)
3.2激活函数
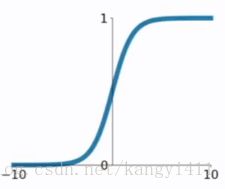
(1)sigmoid
(2)tanh
(3)relu
![]()
relu优势计算速度快、不存在梯度饱和的问题
4、常用实例
梯度下降
一般情况我们求解一个函数的极值是通过求导来求解的,但是有很多函数求导很复杂,且计算器不会求导,计算机是通过试出来的,这种尝试的方式就是梯度下降。
所谓的梯度下降也就是对当前函数针对参数求导,导数乘以步长作为梯度的反方向去下降找到最小误差值点。(梯度下降也可理解为,寻找一个最能找到极值点的方向去移动)
https://www.cnblogs.com/pinard/p/5970503.html
详细内容参考以上文献。
随机梯度下降与批梯度下降
批梯度下降,使用全部样本进行更新,更新速度慢。
随机梯度下降每次选取一个样本来优化权重,方向变化大不一定能很快得到局部最优解
最小二乘法
寻找一条线到所有的点距离最短,采用求导的方式计算
超参数设置
神经网络的层数,一般根据经验来确定。层的节点个数根据公式来定,比如根号nl,或者log。学习率、单批次大小、轮次
softmax
给定多维向量,输出对应的概率
相关学习链接
总体参考技术博客
https://cuijiahua.com/
NLP学习视频
https://www.bilibili.com/video/BV17A411e7qL?p=4
图像识别课程
OpenCV视频教程计算机视觉图像识别从基础到深度学习实战
https://www.bilibili.com/video/BV1uW41117GE?p=8
撰写目的
以最通俗的方式,记录深度学习学习进程,以应用为主。