python实现基本的协同过滤

转载于https://blog.csdn.net/qq_25948717/article/details/81839463

python实现基本的协同过滤

一 理论背景介绍

协同过滤简单来说是利用某兴趣相投、拥有共同经验之群体的喜好来推荐用户感兴趣的信息

（1）确定共现表

如上表：

横坐标，假设有10w部电影，那么横坐标有10w个movie_id

纵坐标，假设有100w个用户，那么纵坐标有100w个user_id

交叉处，“1”代表用户喜爱这部电影

画外音：什么是“喜欢”，需要人为定义，例如浏览过，查找过，点赞过

（2）找到用户A(user_id_1)的兴趣爱好

如上表，可以看到，用户A喜欢电影{m1, m2, m3}

（3）找到与用户A(user_id_1)具有相同电影兴趣爱好的用户群体集合Set

如上表，可以看到，喜欢{m1, m2, m3}的用户，除了u1，还有{u2, u3}
（4）找到该群体喜欢的电影集合Set

如上表，具备相同喜好的用户群里{u2, u3}，还喜好的电影集合是{m4, m5}

画外音：“协同”就体现在这里。

（5）未来用户A(use_id_1)来访问网站时，要推荐电影{m4, m5}给用户A。

二 具体实现步骤

（1）计算两者之间的相似度

通常会先把二维表格绘制在一个图中总，每个用户数据表示一个点。

度量相似度计算的方法：
a.曼哈顿距离计算（计算迅速，节省时间）
b.欧氏距离计算（计算两个点之间的直线距离）

（2）数据预处理

1.下载数据集

ml-latest-small(1MB): http://files.grouplens.org/datasets/movielens/ml-latest-small.zip
ml-latest(234.2MB): http://files.grouplens.org/datasets/movielens/ml-latest.zip

选一个就行，练习一般选小的就行

2.查看movies.csv和ratings.csv文件

movies.csv:

ratings.csv:

3.程序实现

import pandas as pd
movies = pd.read_csv("movies.csv")
ratings = pd.read_csv("ratings.csv")##这里注意如果路径的中文件名开头是r，要转义。
data = pd.merge(movies,ratings,on = 'movieId')#通过两数据框之间的movieId连接
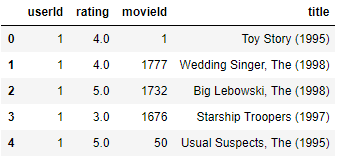
data[['userId','rating','movieId','title']].sort_values('userId').to_csv('data.csv',index=False)
saved_data=pd.read_csv("data.csv")

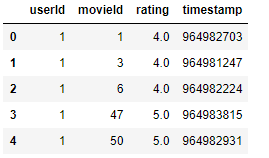
movies.head()

ratings.head()

data.head()

saved_data.head()

saved_data.info()

saved_data.head()

采用python字典来表示每位用户评论的电影和评分

file = open("data.csv",'r', encoding='UTF-8')#记得读取文件时加‘r’， encoding='UTF-8'

##读取data.csv中每行中除了名字的数据

data = {}##存放每位用户评论的电影和评分

for line in file.readlines():
    #注意这里不是readline()
    line = line.strip().split(',')
    #如果字典中没有某位用户，则使用用户ID来创建这位用户
    if not line[0] in data.keys():
        data[line[0]] = {line[3]:line[1]}
    #否则直接添加以该用户ID为key字典中
    else:
        data[line[0]][line[3]] = line[1]
        
#print(data)
#print(data["1"])
file.close()

尝试一下各种line的输出进行理解

# 打开文件
fo = open("data.csv", "r" ,encoding='UTF-8')
print ("文件名为: ", fo.name)
 
for line in fo.readlines()[0:10]:                          #依次读取每行  
    # line = line.strip()                             #去掉每行头尾空白  
    # print("读取的数据为: %s" % (line))
    line = line.strip().split(',')
    print(line)
 
# 关闭文件
fo.close()

计算任何两位用户之间的相似度，由于每位用户评论的电影不完全一样，所以先要找到两位用户共同评论过的电影

然后计算两者之间的欧式距离，最后算出两者之间的相似度

from math import *
def Euclidean(user1,user2):
    #取出两位用户评论过的电影和评分
    user1_data=data[user1]
    user2_data=data[user2]
    distance = 0
    #找到两位用户都评论过的电影，并计算欧式距离
    for key in user1_data.keys():
        if key in user2_data.keys():
            #注意，distance越大表示两者越相似
            distance += pow(float(user1_data[key])-float(user2_data[key]),2)
 
    return 1/(1+sqrt(distance))#这里返回值越小，相似度越大
 
#计算某个用户与其他用户的相似度
def top10_simliar(userID):
    res = []
    for userid in data.keys():
        #排除与自己计算相似度
        if not userid == userID:
            simliar = Euclidean(userID,userid)
            res.append((userid,simliar))
    res.sort(key=lambda val:val[1])
    return res[:10]  # 进行top_n的返回
 
RES = top10_simliar('1')
print(RES)

根据相似度来推荐用户

########################################################################
#根据用户推荐电影给其他人
def recommend(user):
    #相似度最高的用户
    top_sim_user = top10_simliar(user)[0][0]
    #相似度最高的用户的观影记录
    items = data[top_sim_user]
    recommendations = []
    #筛选出该用户未观看的电影并添加到列表中
    for item in items.keys():
        if item not in data[user].keys():
            recommendations.append((item,items[item]))
    recommendations.sort(key=lambda val:val[1],reverse=True)#按照评分排序
    #返回评分最高的10部电影
    return recommendations[:10]  # 返回top_n的推荐电影
 
Recommendations = recommend("1")  # 推荐给用户1
print(Recommendations)

但有时我们会碰到因为两个用户之间数据由于数据膨胀，一方数据大，一方数据小，但是两者成明显的线性关系

我们引入Pearson相关系数来衡量两个变量之间的线性相关性。

Pearson：-1~1   -1：完全负相关  1：完全正相关  0：不相关              

相关系数 0.8-1.0 极强相关

0.6-0.8 强相关

0.4-0.6 中等程度相关

0.2-0.4 弱相关

0.0-0.2 极弱相关或无相关

#########################################################################
##计算两用户之间的Pearson相关系数
def pearson_sim(user1,user2):
    # 取出两位用户评论过的电影和评分
    user1_data = data[user1]
    user2_data = data[user2]
    distance = 0
    common = {}
 
    # 找到两位用户都评论过的电影
    for key in user1_data.keys():
        if key in user2_data.keys():
            common[key] = 1
    if len(common) == 0:
        return 0#如果没有共同评论过的电影，则返回0
    n = len(common)#共同电影数目
    
    print("共同电影数目: %d"%(n))
    print("共同电影: %s"%(common))
 
    ##计算评分和
    sum1 = sum([float(user1_data[movie]) for movie in common])
    sum2 = sum([float(user2_data[movie]) for movie in common])
 
    ##计算评分平方和
    sum1Sq = sum([pow(float(user1_data[movie]),2) for movie in common])
    sum2Sq = sum([pow(float(user2_data[movie]),2) for movie in common])
 
    ##计算乘积和
    PSum = sum([float(user1_data[it])*float(user2_data[it]) for it in common])
 
    ##计算相关系数
    num = PSum - (sum1*sum2/n)
    den = sqrt((sum1Sq-pow(sum1,2)/n)*(sum2Sq-pow(sum2,2)/n))
    if den == 0:
        return 0
    r = num/den
    return r
 
R = pearson_sim('1','3') # 两用户之间的Pearson相关系数
print("两用户之间的Pearson相关系数: %f"%(R))