从前有一条河,河的左岸有m个传教士(Missionary)和m个野人(Cannibal),和一艘最多可乘n人的小船。约定左岸,右岸和船上或者没有传教士,或者野人数量少于传教士,否则野人会把传教士吃掉。
编程,接收m和n,搜索一条可让所有的野人和传教士安全渡到右岸的方案。
我们先假设左岸有3个传教士和3个野人,小船最多可乘2人。把当前左岸的状态抽象为:
(3,3,1)
前两个"3"代表左岸有3个传教士和3个野人,1代表船在左岸。把每一次可行的渡船方案作为算符。比如,在初始状态,让1个传教士和1个野人上船并渡到右岸,这一算符可表示为:
(1,1)
算符的两位数分别代表要移动的传教士,野人的数量;把人移到没有船的岸边并且改变状态向量中船的值。
对于固定大小的小船,算符的数量是一定的:
class Move {
public :
int missionary; // 要移动的传教士数量
int cannibal; // 野人
};
class MoveGroup {
public :
Move move[500]; // 算符集
int numMove; // 可用算符的总数
MoveGroup(int MAX_ON_BOAT) { // 利用构造器求算符集
int m, c, i = 0;
for (m = 0; m <= MAX_ON_BOAT; m++)
for (c = 0; c <= MAX_ON_BOAT; c++)
if (c==0 && m!=0) {
move[i].missionary=m;
move[i].cannibal=0;
i++;
}
else if (m==0 && c!=0) {
move[i].missionary=0;
move[i].cannibal=c;
i++;
}
else if (m+c<=MAX_ON_BOAT && m+c!=0 && m>=c) {
move[i].missionary = m;
move[i].cannibal = c;
i++;
}
numMove = i;
}
};
创建一个MoveGroup 对象
MoveGroup mg(2);
即可得到当小船最多可乘2人时的算符集。
这个程序所要做的,就是通过这个已知的算符集,将初始状态(3,3,1)转变为最终状态(0,0,0)。我们应将状态作为搜索的元素。
构建类时应注意,并不是每个算符对于任意的状态都是可以应用的,这需要对应用算符后的安全性进行检查,以判断这一算符对当前状态是否可用;同时,类中也要包含一个判断当前状态是否是最终节点(0,0,0)的方法;当然”==”,”=”这两个运算符以及null值,这是调用dso.h时所不可或缺的。(详见源文件)
class ElemType : Move { // 继承 Move 类,获得传教士,野人数据成员。
private :
bool boat; // 船是否在左岸?
public :
ElemType* flag; // 这个后边再说,暂时用不到
ElemType(int MAX_PEOPLE) { // 创建初始状态
missionary = cannibal = MAX_PEOPLE;
boat = true;
flag = NULL;
}
ElemType() {}
bool operator ==(ElemType e) {
return this->missionary==e.missionary &&
this ->cannibal==e.cannibal &&
this ->boat==e.boat;
}
void operator =(ElemType e) {
this->missionary = e.missionary;
this->cannibal = e.cannibal;
this->boat = e.boat;
this->flag = e.flag;
}
ElemType friend operator >>(ElemType source, Move &mv) {
// 移动操作,通过重载运算符 “>>” ,你将在 isSafe(ElemType) 中见到用法。
ElemType result;
if(source.boat == 1) {
result.missionary = (source.missionary -= mv.missionary);
result.cannibal = (source.cannibal -= mv.cannibal);
result.boat = 0;
} else {
result.missionary = (source.missionary += mv.missionary);
result.cannibal = (source.cannibal += mv.cannibal);
result.boat = 1;
}
return result;
}
bool isSafe(Move &mv, int MAX_PEOPLE) {
// 判断当前状态在进行 mv 操作后还是不是安全状态
if( (boat==1&&(missionary-mv.missionary < 0 ||
cannibal-mv.cannibal < 0)) ||
(boat==0&&(missionary+mv.missionary > MAX_PEOPLE ||
cannibal+mv.cannibal > MAX_PEOPLE)) )
return false;
else {
ElemType temp = *this >> mv;
if( temp.missionary==0 || temp.missionary==MAX_PEOPLE ||
(temp.missionary>=temp.cannibal &&
MAX_PEOPLE-temp.missionary >= MAX_PEOPLE-temp.cannibal))
return true;
else return false;
}
}
bool isSuccess() { return missionary==0 && cannibal==0 && boat==0; }
//isSuccess() 判断当前状态是否为最终节点
int getM() { return missionary; }
int getC() { return cannibal; }
int getB() { return boat; }
void print() {
cout <<'('<< missionary <<','<< cannibal
<<','<< boat <<')' << endl;
}
};
const ElemType null(0); //(0,0,1) 这是不会出现的
void print(ElemType &e) { e.print(); } // 打印函数
至此,我们已经完成了对问题的描述。
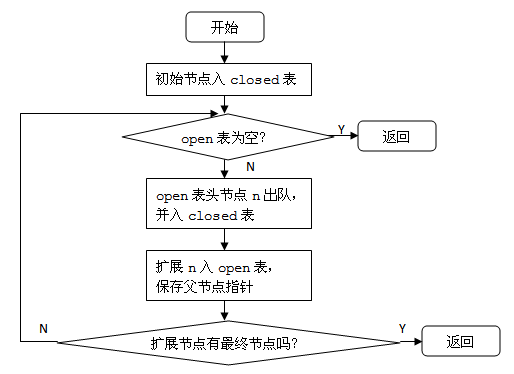
搜索过程采用较简单的“宽度优先盲目搜索”,算法框图如下:
#include "dso.h"
typedef ElemType Status;
当得到了一个最终节点(0,0,0)时,如果我们前边的操作没有保存路径的话,那么我们就只知道这个问题有解,而不知道解的具体路径。还记得在定义ElemType时那个旗子指针吗,用它保留它的父节点的地址,问题就解决了。
open,closed表均通过队列实现。由于对扩展节点要保存指针,所以closed表需要一个获得尾指针的方法。
class Queuex : public Queue {
public :
ElemType* getTailPtr() {
if(Queue::isEmpty()) return NULL;
QNode* temp = front->next;
while(temp != rear) {
if(temp->next == rear) return &temp->next->node;
temp = temp->next;
}
return &temp->node;
}
};
搜索得到的答案也保存在一个队列里,但我们知道:当得到一个最终节点时,根据它的指向父节点的指针向上搜索得到的是一个反的解序列,这里使用一个临时的栈,可以将解的顺序调换过来。
class Answer : public Queue {
private :
int max_people;
public :
Answer(int MAX_PEOPLE, int MAX_ON_BOAT) {
Queue open;
Queuex closed;
Stack temp; // 这是所使用的临时栈
Status s0(MAX_PEOPLE); // 这是初始节点
MoveGroup mg(MAX_ON_BOAT); // 这是算符集
// 以下是搜索算法:
open.enqueue(s0);
max_people = MAX_PEOPLE;
while(!open.isEmpty()) {
Status s1 = open.dequeue(), s2;
closed.enqueue(s1);
ElemType* ptr = closed.getTailPtr();
// 得到被扩展的父节点的指针 ptr
for(int i = 0; i < mg.numMove; i++)
if( s1.isSafe(mg.move[i], MAX_PEOPLE) ) {
s2 = s1 >> mg.move[i];
if(closed.locate(s2) == INFEASIBLE) {
s2.flag = ptr; open.enqueue(s2);
}
if(s2.isSuccess()) {
// 搜索到最终节点后的操作
closed.enqueue(s2);
while(s2.flag != NULL) {
temp.push(s2); s2 = *(s2.flag);
}
this->enqueue(s0);
while(!s2.isSuccess()) {
s2 = temp.pop(); this->enqueue(s2);
}
return;
}
}
}
}
void show() { this->traverse(print); }
};
就要成功了,通过下面这个声明就可以得到MAX_PEOPLE个传教士,MAX_PEOPLE个野人,每艘船上最多乘坐MAX_ON_BOAT人的解:
Answer answer(MAX_PEOPLE, MAX_ON_BOAT);
通过下面的调用可以列出整个解的过程:
answer.show();
源程序 >>> (在控制台输入MAX_PEOPLE和MAX_ON_BOAT,然后输出mco.log演示移动过程)
以前编过一个C语言版的,不过似乎有内存泄漏的八哥,这个版本应该是没问题了。
完成于2006年6月18日
