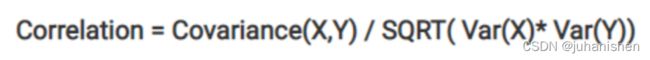EDA（Explore Data Analysis）一步一步详解

EDA

EDA 是 Explore Data Analysis 的缩写，是机器学习处理数据的第一步。它影响建模的质量或准确性。下面的这篇来之Analytics Vidhya的博客写得浅显易懂。所以，尽可能翻译或做笔记。

• A Comprehensive Guide to Data Exploration

总览

• 有关数据探索（EDA）的完整教程
• 我们涵盖了数据探索的几个方面，包括缺失值估算，异常值去除和特征工程的技巧。

介绍

没有数据探索分析的捷径。 If you are in a state of mind, that machine learning can sail you away from every data storm, trust me, it won’t. 经过一段时间后，您会意识到自己正在努力提高模型的准确性。 在这种情况下，数据探索技术将助您一臂之力。

我可以自信地说，因为我经历过很多这样的情况。

我从事商业数据分析专业近三年了。 在我最初的日子里，我的一位导师建议我花大量时间在探索和分析数据上。 遵循他的建议对我很有帮助。

我创建了本教程是为了帮助您了解数据探索的基础技术。 与往常一样，我尽力以最简单的方式解释这些概念。 为了更好地理解，我举了几个例子来说明复杂的概念。本翻译尽量保持原文的原汁原味，翻译不出的地方，附上原文。

目录

1. 数据探索和准备步骤
2. 数据缺失处理
   • 为什么需要数据缺失处理？
   • 为什么数据会丢失？
   • 哪些方法可以处理缺失数据？
3. 异常值的检测和处理技术
   • 什么是异常值?
   • 异常值类型?
   • 什么是造成异常值的原因?
   • 异常值对数据集的影响?
   • 怎样检测异常值?
   • 怎样删除异常值?
4. 特征工程的艺术
   • 什么是特征工程?
   • 特征工程的过程是什么?
   • 什么是变量转换?
   • 什么时候我们需要变量转换?
   • 什么是变量转换的常用方法?
   • 什么是特征变量的创建和好处?

让我们开始吧!

1. 数据探索和准备步骤

记住输入的质量决定输出的质量。 因此，一旦您准备好业务假设，就可以在这里花费大量时间和精力。 据我个人估计，数据探索，清理和准备工作可能会占用您整个项目总时间的70％。

以下是理解，清理和准备数据以构建预测模型所涉及的步骤：

1. 变量识别
2. 单变量分析
3. 双变量分析
4. 数据缺失处理
5. 异常值处理
6. 变量转换
7. 变量创建

最后，我们需要反复进行第4步至第7步，才能得出完善的模型。

现在，我们详细研究每个阶段：

1. 变量识别

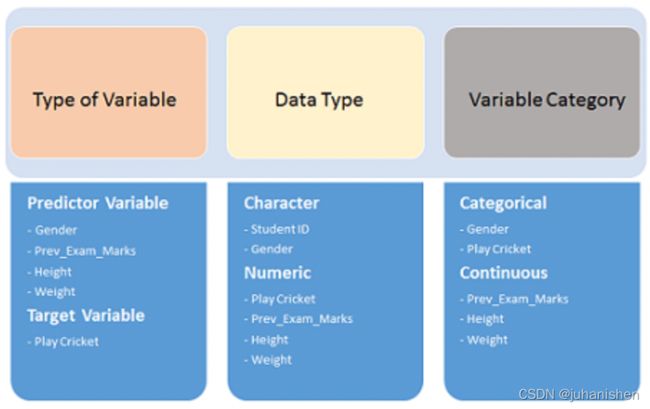
首先，确定Predictor（输入）和Target（输出）变量。 接下来，确定变量的数据类型和类别。

通过举例，让我们更清楚地了解此步骤。

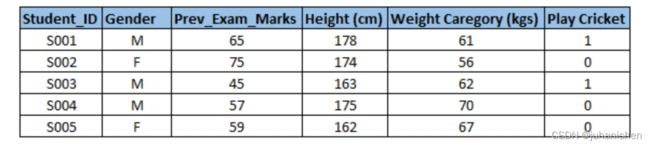
示例：-假设我们要预测学生是否会打板球（请参阅下面的数据集）。 在这里，您需要确定预测变量，目标变量，变量的数据类型和变量类别。 

下面，变量已在不同类别中定义： 

 2. 单变量分析

在此阶段，我们逐一探讨变量。 执行单变量分析的方法将取决于变量类型是分类类型还是连续类型。 让我们分别查看分类和连续变量的这些方法和统计指标：

• 连续变量：-在连续变量的情况下，我们需要了解变量的集中趋势和分布。 使用各种统计指标可视化方法对这些指标进行测量，如下所示： 

• [注意]：单变量分析还用于强调缺省值和异常值。在本系列的下一部分中，我们将介绍处理缺省值和异常值的方法。要了解有关这些方法的更多信息，可以参考Udacity的课程描述性统计学。

• 分类变量：-对于分类变量，我们将使用频率表来了解每个类别的分布。我们还可以将其理解为每个类别下的值的百分比。可以使用两个指标（针对每个类别的计数和计数％）进行度量。条形图可以用作可视化。

3. 双变量分析

双变量分析找出两个变量之间的关系. Here, we look for association and disassociation between variables at a pre-defined significance level. 我们可以对分类变量和连续变量的任何组合执行双变量分析。组合可以是：分类和分类，分类和连续以及连续和连续。在分析过程中使用了不同的方法来解决这些组合。

让我们详细了解可能的组合：

连续和连续：在两个连续变量之间进行双变量分析时，我们应该查看散点图。找出两个变量之间的关系是一种很不错的方法。散点图的模式指示变量之间的关系。该关系可以是线性的或非线性的。

散点图显示了两个变量之间的关系，但并不表示它们之间关系的强度。 为了找到关系的强度，我们使用"相关"。 相关的范围在-1和+1之间变化。

-1：完美的负线性相关
+1：完美的正线性相关和
0：无相关

可以使用以下公式得出相关性：

相关 = 协方差(X,Y) / SQRT(Var(X)* Var(Y) )

Note: 

协方差公式参考, 

方差公式参考, 

Pearson 参数公式, 

=

Person参数链接

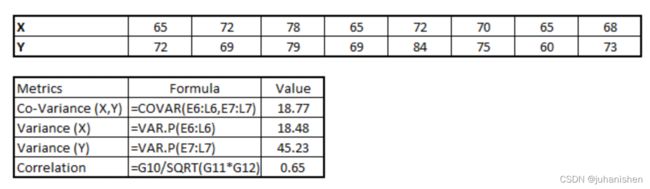
各种工具具有识别变量之间相关性的功能。 在Excel中，函数CORREL()用于返回两个变量之间的相关性，而SAS使用过程PROC CORR来识别相关性。 这些函数返回Pearson Correlation值以标识两个变量之间的关系：

 在上面的示例中，我们在两个变量X和Y之间具有良好的正关系（0.65).

分类和分类：要查找两个分类变量之间的关系，我们可以使用以下方法：

• Two way Table(双向表)：我们可以通过创建一个计数和计数％双向表来开始分析关系。 行代表一个变量的类别，列代表另一变量的类别。 我们显示行和列类别的每种组合中可用的观测值的计数或计数％。

• Stacked Column Chart(堆积柱形图)：此方法更像是双向表的可视形式。 

• Chi-Square Test(卡方检验)：该检验用于得出变量之间关系的统计显着性。 此外，它还测试了样本中的证据是否足够强大，可以概括出更大人群之间的关系。 卡方是基于双向表中一个或多个类别中的预期频率和观测频率之间的差异。 它以自由度返回计算出的卡方分布的概率。

  概率为0：表示两个类别变量都是因变量

  概率为1：表明两个变量都是独立的。

  概率小于0.05：表明变量之间的关系在95％置信度下很显着。 用于检验两个类别变量的独立性的卡方检验统计量如下：
  
  其中O代表观察到的频率。 E是零假设下的期望频率，并通过以下公式计算：

  

从以前的Two-way Table(双向表)中，the expected count for product category 1 to be of small size is 0.22. It is derived by taking the row total for Size (9) times the column total for Product category (2) then dividing by the sample size (81). 这是对每个单元格进行计算。Statistical Measures used to analyze the power of relationship are:

• Cramer’s V for Nominal Categorical Variable Mantel-Haenszed Chi-Square for ordinal categorical variable.

• Different data science language and tools have specific methods to perform chi-square test. In SAS, we can use Chisq as an option with Proc freq to perform this test.

分类和连续：While exploring relation between categorical and continuous variables, we can draw box plots for each level of categorical variables. If levels are small in number, it will not show the statistical significance. To look at the statistical significance we can perform Z-test, T-test or ANOVA.

• Z-Test/ T-Test:- Either test assess whether mean of two groups are statistically different from each other or not.
  
  

If the probability of Z is small then the difference of two averages is more significant. The T-test is very similar to Z-test but it is used when number of observation for both categories is less than 30.

• ANOVA:- It assesses whether the average of more than two groups is statistically different.

示例：假设我们要测试五种不同锻炼的效果。 为此，我们招募了20名男性，并将一种运动类型分配给4名男性（5组）。 几周后记录他们的体重。 我们需要找出这些练习对他们的影响是否显着不同。 这可以通过比较5组（每组4个人）的体重来完成。

到这里为止，我们已经了解了数据探索，变量识别，单变量和双变量分析的前三个阶段。 我们还研究了各种统计和视觉方法来识别变量之间的关系。

现在，我们将研究缺失值处理的方法。 更重要的是，我们还将研究为什么数据中会出现缺失值以及为何需要对它们进行处理。

2. 数据缺失处理

2.1&1.4 为什么需要数据缺失处理

训练数据集中的数据丢失会降低模型的Power/fit(功效/拟合度)，或者会导致模型产生偏差，因为我们没有正确分析行为和与其他变量的关系。 它可能导致错误的预测或分类。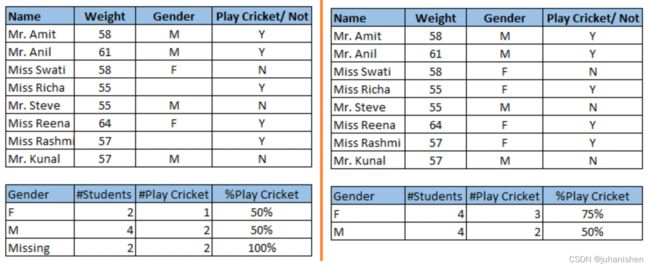

 注意上图所示的缺失值：在左图中，我们没有处理缺失值。从该数据集得出的结论是，男性打板球的机会高于女性。另一方面，如果您查看第二张表，该表显示了在处理了缺失值之后的数据（基于性别），我们可以发现，与男性相比，女性打板球的机会更高。

为什么我的数据会丢失？

我们研究了处理数据集中缺失值的重要性。现在，让我们确定出现这些缺失值的原因。它们可能发生在两个阶段：

• 数据提取：提取过程可能存在问题。在这种情况下，我们应该与data guardians(数据监护人)一起仔细检查数据是否正确。一些hashing(散列)过程也可以用来确保数据提取正确。数据提取阶段的错误通常很容易发现，并且也很容易纠正。

• 数据收集：这些错误发生在数据收集时，很难纠正。它们可以分为四种类型：

  • Missing completely at random(完全随机丢失)：所有变量的丢失概率相同时，就是这种情况。例如：respondents of data collection process decide that they will declare their earning after tossing a fair coin. If an head occurs, respondent declares his / her earnings & vice versa. Here each observation has equal chance of missing value.(数据收集过程的受访者决定，他们将在投入公平硬币后宣布其收入。如果发生正面冲突，受访者会宣布其收入，反之亦然。在这里，每个观察值都有相等的机会失去价值。)

  • Missing at random(随机缺失)：当变量随机缺失且缺失比率随其他输入变量的不同值/水平而变化时，会出现这种情况。例如：我们正在收集年龄数据，女性比男性丢失数据的概率更高。

  • Missing that depends on unobserved predictors(缺失取决于未观察到的预测变量)：当缺失值不是随机值且与未观察到的输入变量相关时，会出现这种情况。例如：在医学研究中，如果特定的诊断引起不适，则退出研究的机会更高。除非我们将“不适”作为所有患者的输入变量，否则该缺失值不是随机的。

  • Missing that depends on the missing value itself(缺失取决于缺失值本身)：缺失值的概率与缺失值本身直接相关时就是这种情况。例如：收入较高或较低的人可能不愿意回答他们的收入。

2.3 处理丢失数据的方法

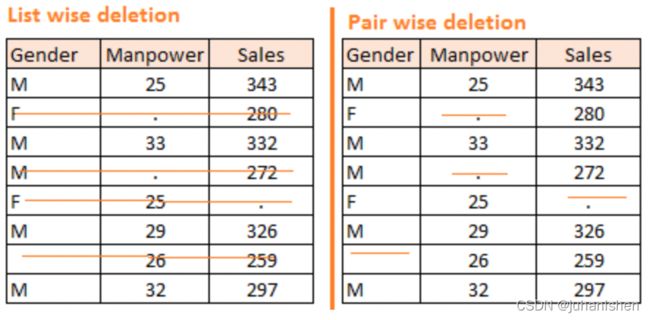
1. Deletion: It is of two types: List Wise Deletion and Pair Wise Deletion.

   • In list wise deletion, we delete observations where any of the variable is missing. Simplicity is one of the major advantage of this method, but this method reduces the power of model because it reduces the sample size.

   • In pair wise deletion, we perform analysis with all cases in which the variables of interest are present. Advantage of this method is, it keeps as many cases available for analysis. One of the disadvantage of this method, it uses different sample size for different variables.
     

   • Deletion methods are used when the nature of missing data is "Missing completely at random" else non random missing values can bias the model output.

2. Mean/ Mode/ Median Imputation (均值/众数/中位数插补)： 插补是一种用估计值填充缺失值的方法。目的是采用可以在数据集的有效值中识别的已知关系，以帮助估计缺失值。均值/众数/中位数插补是最常用的方法之一。它包括用该变量所有已知值的均值或中位数（定量属性）或众数（定性属性）替换给定属性的缺失数据。它可以有两种类型：

   • Generalized Imputation(广义归因)：在这种情况下，我们计算该变量所有非缺失值的均值或中位数，然后用均值或中位数替换缺失值。像上表一样，缺少变量“ Manpower”，因此我们取“ Manpower”的所有非缺-失值的平均值（28.33），然后用它替换缺失值。

   • Similar case Imputation(相似情况的推算)：在这种情况下，我们分别计算性别“男”（29.75）和“女”（25）的平均值，这些平均值均不含缺失值，然后根据性别替换缺失值。对于“男性”，我们将缺失的人力值替换为29.75，对于“女性”将替换为25。

3. 预测模型：预测模型是用于处理丢失数据的复杂方法之一。在这里，我们创建了一个预测模型来估计将替代缺失数据的值。在这种情况下，我们将数据集分为两组：一组没有缺失值，另一组有缺失值。第一个数据集成为模型的训练数据集，而具有缺失值的第二个数据集是测试数据集，具有缺失值的变量被视为目标变量。接下来，我们基于训练数据集的其他属性创建一个模型来预测目标变量并填充测试数据集的缺失值，我们可以使用回归，ANOVA，Logistic回归和各种建模技术来执行此操作。这种方法有两个缺点：

   • 1. 模型估计值通常比真实值表现得更好
   • 1. 如果数据集中的属性与缺少值的属性之间没有关系，则该模型将无法精确估计缺失值。

4. KNN插补：在这种插补方法中，使用给定数量的属性来插补属性的缺失值，这些属性与缺失值的属性最相似。使用距离函数确定两个属性的相似性。已知该方法具有某些优点和缺点。

   • 好处：
     • k近邻可以预测定性和定量属性
     • 不需要为每个缺少数据的属性创建预测模型
     • 具有多个缺失值的属性可以轻松处理
     • 数据的相关结构已经被考虑
   • 坏处：
     • 在分析大型数据库时，KNN算法非常耗时。它搜索所有数据集以查找最相似的实例。
     • k值的选择非常关键。 k的较高值将包含与我们需要的属性明显不同的属性，而k的较低值意味着缺少重要属性。

   处理缺失值之后，下一个任务是处理异常值。通常，我们在构建模型时往往会忽略异常值。这是令人沮丧的做法。异常值往往会使您的数据偏斜并降低准确性。让我们进一步了解异常值处理。

3&1.5 异常值的检测和处理技术

3.1 什么是异常值

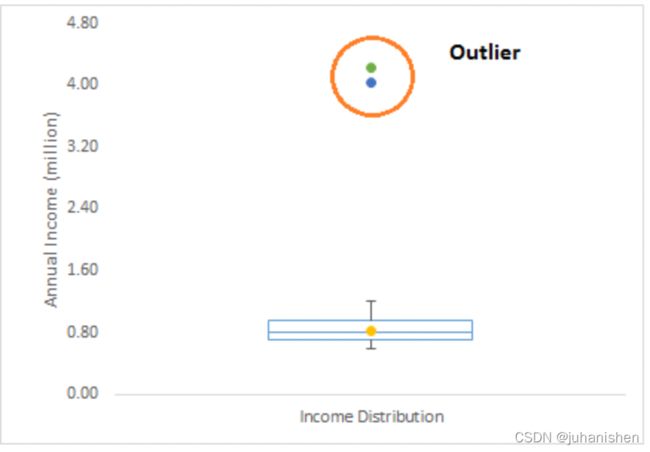
异常值是分析人员和数据科学家常用的术语，因为它需要密切关注，否则可能导致错误的估计。 简而言之，异常值是一个观察值，与样本的整体模式相距甚远。

让我们举一个例子，我们进行客户分析，发现客户的平均年收入为80万美元。 但是，有两个客户的年收入分别为4百万美元和420万美元。 这两个客户的年收入远高于其余人口。 这两个观察结果将被视为离群值。

3.2 异常值类型

异常值可以有两种类型：单变量和多变量。 上面，我们讨论了单变量异常值的示例。 当我们查看单个变量的分布时，可以发现这些异常值。 多元异常值是n维空间中的异常值。 为了找到它们，您必须查看多维分布。

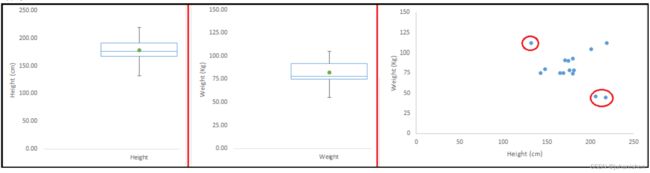
让我们通过一个例子来理解这一点。 让我们说我们正在理解身高和体重之间的关系。 下面，我们有身高，体重的单变量和双变量分布。 看一下箱形图。 我们没有任何异常值（高于或低于1.5 * IQR，这是最常见的方法）。 现在查看散点图。 在这里，在特定的体重和身高段中，我们有两个低于平均值的值，另一个高于平均值。 

3.3 什么是造成异常值的原因

每当我们遇到异常值时，解决它们的理想方法是找出出现这些异常值的原因。处理它们的方法将取决于它们发生的原因。异常原因可以分为两大类：

• 人工（错误）/非自然
• 自然。

让我们更详细地了解各种异常值

• 数据输入错误：-人为错误，例如在数据收集，记录或输入过程中引起的错误，可能导致数据异常。例如：客户的年收入为100,000美元。偶然地，数据输入运算符在图中添加了一个额外的零。现在收入变成$ 1,000,000，是原来的10倍。显然，与其他人口相比，这是异常值。

• 测量误差：这是异常值的最常见来源。原因是所使用的测量仪器出现故障。例如：有10台称重机。其中9项是正确的，1项是错误的。由故障机器上的人员测量的体重将比组内其他人员高/低。在故障机器上测得的重量可能导致异常值。

• 实验误差：异常值的另一个原因是实验误差。例如：在一个由7名选手组成的100m冲刺中，一名选手对于"出发"的口令迟疑了一会儿，这导致他起步较晚。因此，这导致该名运动员的跑步时间比其他跑步者更长。他的总跑步时间可能出现异常值。

• 故意离群值：通常在涉及敏感数据的自我报告测度中发现。例如：青少年通常会少报他们所消耗的酒精量。他们中只有一小部分会报告实际消耗。在这里实际值可能看起来像是离群值，因为其余的青少年正在少报了消耗量。

• 数据处理错误：无论何时执行数据挖掘，我们都会从多个来源提取数据。某些操作或提取错误可能会导致数据集中出现异常值。

• 抽样误差：例如，我们必须测量运动员的身高。错误地，我们在样本中包括了一些篮球运动员。这种包含可能会导致数据集中出现异常值。

• 自然异常值：当异常值不是人为（由于错误）时，它是自然异常值。例如：在我与一家著名的保险公司的最后一份工作中，我注意到前50名财务顾问的表现远远高于其他人群。令人惊讶的是，这不是由于任何错误。因此，每当我们与顾问一起执行任何数据挖掘活动时，我们就分别对待这一部分。

3.4 异常值对数据集的影响

异常值可以极大地改变数据分析和统计建模的结果。 数据集中的异常值有许多不利影响：

• 它增加了误差方差并降低了统计检验的功效
• 如果异常值是非随机分布的，则它们可以降低正态性
• 它们可能会偏向或影响可能具有实质意义的估计
• 它们还会影响回归，ANOVA和其他统计模型假设的基本假设。

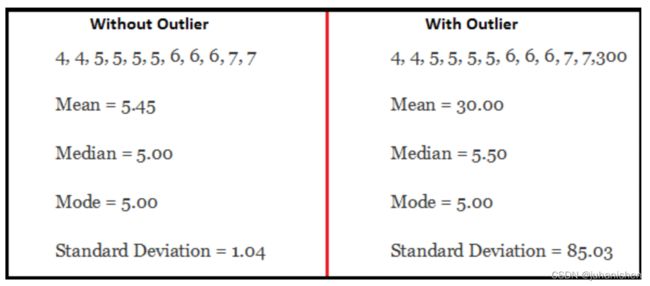
为了深入了解其影响，让我们举一个例子来检查在数据集中有无异常的情况下数据集会发生什么情况。

例： 

如您所见，具有异常值的数据集的均值和标准差明显不同。 在第一种情况下，我们说平均值为5.45。 但是随着异常值的出现，平均价格飙升至30。这将完全改变估计值。

3.5 怎样检测异常值？

检测异常值的最常用方法是可视化。我们使用各种可视化方法，例如箱形图，直方图，散点图（上面，我们使用箱形图和散点图进行可视化）。一些分析师还使用各种经验法则来检测异常值。他们之中有一些是：

• 任何值，超出-1.5 x IQR到1.5 x IQR的范围,( 补充:IQR(四分位距) 的定义在百度百科有很好的描述)
• 使用上限方法。任何超出第5个百分点和第95个百分点范围的值都可以视为异常值
• 距离均值三个或三个以上标准偏差的数据点被视为异常值
• 异常值检测只是检查有影响的数据点的数据的一种特殊情况，它还取决于业务理解
• 双变量和多变量离群值通常使用影响力或杠杆或距离的指数进行度量。诸如Mahalanobis的距离和Cook D之类的流行指标经常被用来检测异常值。
• 在SAS中，我们可以使用PROC Univariate，PROC SGPLOT。为了识别异常值和有影响力的观察结果，我们还研究了统计量度，例如学生，COOKD，RSTUDENT等。

3.6 怎样删除异常值？

处理异常值的大多数方法与缺失值的方法类似，例如删除观察值，对其进行转换，将它们进行装箱，将它们视为单独的组，估算值和其他统计方法。 在这里，我们将讨论用于处理异常值的常用技术：

• 删除观察值：如果是由于数据输入错误，数据处理错误或异常观察值数量很小而导致的异常值，我们将删除它们。 我们还可以在两端使用修剪来去除异常值。

• 转换和合并值：转换变量还可以消除异常值。 值的自然对数可减少由极值引起的变化。 分箱也是变量转换的一种形式。 决策树算法可以很好地处理因变量合并而造成的异常值。 我们还可以使用将权重分配给不同观察值的过程。 

估算：像估算缺失值一样，我们也可以估算异常值。 我们可以使用均值，中位数，模态插补方法。 在估算值之前，我们应该分析它是自然异常值还是人为异常值。 如果是人为的，我们可以采用估算值。 我们还可以使用统计模型来预测异常值，然后再将其与预测值一起使用。

单独处理：如果存在大量异常值，则应在统计模型中对其进行单独处理。 一种方法是将两个组视为两个不同的组，并为两个组建立单独的模型，然后组合输出。

到这里，我们已经了解了数据探索的步骤，缺失值处理以及异常值检测和处理的技术。 这三个阶段将使您的原始数据在信息可用性和准确性方面更好。 现在，我们进入数据探索的最后阶段。 这是特征工程。

4 特征工程的艺术

4.1 什么是特征工程?

特征工程是从现有数据中提取更多信息的科学（和艺术）。 您没有在此处添加任何新数据，但实际上是在使已有的数据更有用。

例如，假设您正在尝试根据日期来预测购物中心的人跌倒数目。 如果您尝试直接使用日期，则可能无法从数据中提取有意义的见解。 这是因为脚下坠落受到的影响要小于星期几。 现在，有关星期几的信息已隐含在您的数据中。 您需要提取它出来使您的模型更好。

这种从数据中提取信息的练习称为特征工程。

4.2 特征工程的过程是什么?

一旦完成了数据探索的前5个步骤，即可以执行特征工程-变量识别，单变量，双变量分析，缺失值插补和异常值处理。 特征工程本身可以分为两个步骤：

• 变量转换。
• 变量/特征创建。

这两种技术在数据探索中至关重要，并且对预测的能力具有显着影响。 让我们详细了解每个步骤。

4.3&1.6 什么是变量转换?

在数据建模中，转换是指用函数替换变量。 例如，用变量x的平方/立方根或对数函数来替换变量x叫做一种转换。 换句话说，变换是改变变量与其他变量的分布或关系的过程。

让我们看一下变量转换很有用的情况。

4.4 什么时候我们需要变量转换?

以下是需要进行变量转换的情况：

• 当我们想要更改变量的标度或标准化变量的值以更好地理解时。 如果必须使用不同比例的数据，则必须进行此转换，但是此转换不会更改变量分布的形状

• 当我们可以将复杂的非线性关系转换为线性关系时。 与非线性或曲线关系相比，变量之间线性关系的存在更容易理解。 变换帮助我们将非线性关系转换为线性关系。 散点图可用于查找两个连续变量之间的关系。 这些转换也改善了预测。 对数转换是在这些情况下使用的常用转换技术之一。

• 对称分布优于倾斜分布，因为它更易于解释和生成推论。 一些建模技术需要变量的正态分布。 因此，只要分布偏斜，就可以使用减少偏斜的变换。 对于右偏分布，我们采用变量的平方/立方根或对数，对于左偏分布，我们采用变量的平方/立方或指数。 

• 从实施的角度（人工参与）也可以使用变量转换。 让我们更清楚地了解它。 在我的一个有关员工绩效的项目中，我发现年龄与员工绩效有直接关系，即年龄越高，绩效越好。 从实施的角度来看，启动基于年龄的程序可能会带来实施方面的挑战。 但是，将销售代理商分为三个年龄段，分别是<30岁，30-45岁和> 45岁，然后为每个群体制定三种不同的策略是明智的方法。 这种分类技术称为变量合并。

4.5 什么是变量转换的常用方法?

有多种用于转换变量的方法。正如讨论的那样，其中一些包括平方根，立方根，对数，binning(分档)，倒数等。让我们通过重点介绍这些转换方法的优缺点来详细研究这些方法。

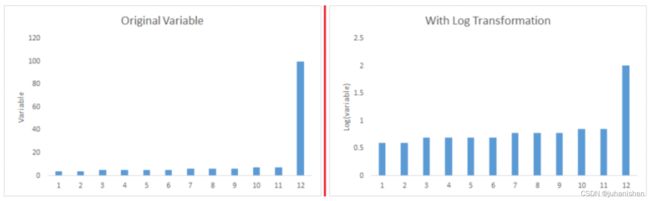
• 对数：变量的对数是一种常用的转换方法，用于更改变量在分布图中的分布形状。通常用于减少变量的右偏度。不过，它也不能应用于零或负值。

• 平方根/立方根：变量的平方根和立方根对变量分布具有良好的影响。但是，它不如对数转换那么重要。多维数据集根有其自身的优势。它可以应用于包括零在内的负值。平方根可以应用于包括零的正值。

• 分档：用于对变量进行分类。它是对原始值，百分位数或频率执行的。分类技术的决策基于业务理解。例如，我们可以将收入分为三类，即：高，平均和低。我们还可以根据多个变量的值执行协变量(co-variate binning)合并。

4.6 & 1.7 什么是特征变量的创建和好处?

特征/变量创建是一个基于现有变量生成新变量/特征的过程。 例如，假设我们将date（dd-mm-yy）作为数据集中的输入变量。 我们可以生成可能与目标变量具有更好关系的新变量，如日，月，年，周，周日。 此步骤用于突出显示变量中的隐藏关系：

有多种创建新功能的技术。让我们看一些常用的方法：

• 创建派生变量：这是指使用一组函数或不同方法从现有变量中创建新变量。让我们通过“泰坦尼克号-Kaggle竞赛”来看看。在此数据集中，年龄变量有缺失值。为了预测缺失值，我们使用名称的称呼（主人，先生，小姐，夫人）作为新变量。我们如何决定要创建哪个变量？老实说，这取决于业务人员对分析师的理解，他的好奇心以及他可能对该问题有的一套假设。也可以使用诸如获取变量日志，变量分档和其他变量转换方法之类的方法来创建新变量。

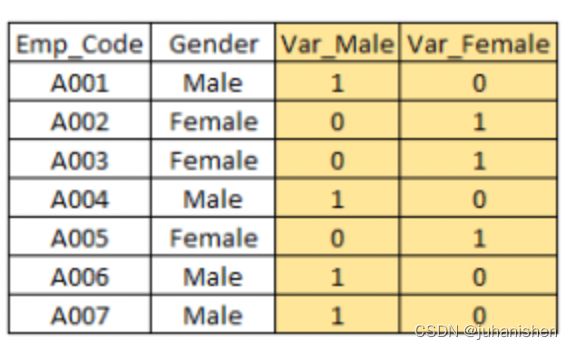
• 创建虚拟变量：虚拟变量最常见的应用之一是将分类变量转换为数字变量。虚拟变量也称为指标变量。在统计模型中将分类变量用作预测变量很有用。分类变量的值可以为0和1。我们以变量“性别”为例。我们可以产生两个变量，分别是"Var_Male" (值1 (男性)和0 (无男性) )和" Var_Female"(值1) (女性)和 0 (无女性)。我们还可以为具有n或n-1个虚拟变量的两类以上的分类变量创建虚拟变量。

为了进一步阅读，这里列出了可以应用于您的数据的转换/创建想法。

尾注

如开头所述，在数据探索中投入的质量和精力将好模型与坏模型区分开。

这样就结束了我们关于数据探索和准备的指南。 在这份综合指南中，我们详细研究了数据探索的七个步骤。 本系列文章的目的是为数据科学中极为重要的过程提供深入的逐步指导。

就个人而言，我很喜欢编写本指南，并希望从您的反馈中学习。 您觉得本指南有用吗？ 非常感谢您的建议/反馈。 请随时通过以下评论提出您的问题。