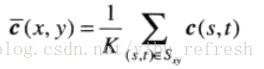数字图像处理第六章彩色图像处理(颜色模型,伪彩色图像处理,全彩色图像处理,彩色图像分割、彩色图像边缘检测,后续补充)
本章节主要内容包括彩色模型分类、伪彩色图像处理、全彩色图像处理、彩色变换、彩色图像的基本变换、彩色图像的平滑和锐化、基于彩色图像的分割、噪声、压缩。
6.1彩色模型
颜色模型又叫颜色空间或者颜色系统,其目的是在某些标准下用通常可以接受的方式方便地对彩色加以说明。
本质上彩色模型是坐标系统和子空间的说明,其中,位于系统中的每个颜色都由单个点来表示。
主要由 RGB\HSI\CMY\CMYK四种颜色空间。
6.1.1RGB颜色模型
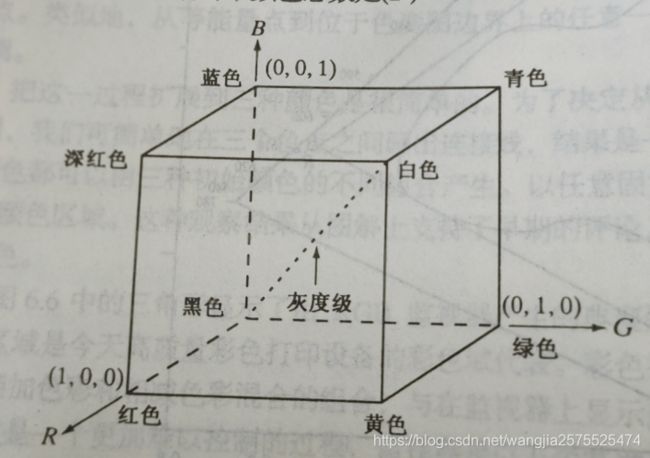
该种模型基于笛卡尔坐标,坐标轴为红绿蓝三基色;
该模型的彩色子空间是一个立方体,其中RGB位于3个角上;二次色青色、深红色、黄色位于其他三个角上面,黑色位于原点处,白色位于离原点最远的角上。其中灰度变换沿着黑色到白色点的斜线上。
该模型中,不同颜色的是位于立方体上或内部的点,且由自原点延伸的向量来定义的。
RGB由三个颜色分量组成,每个颜色分量是8比特深度,3个总共加起来为24比特的深度;因此,全彩色图像通常是一副24比特的RGB图像。
6.1.2、CMY和CMYK彩色模型
该模型的基色为青色、深红色、黄色,这三个色是光的二次色,是颜料的原色。
例如,当青色颜料涂覆的表面用白光照射时,该表面将不反射红光。也就是说,青色从反射的白光中减去红光,白光本身由等量的红光、绿光、蓝光组成。
RGB和CMY的转换:
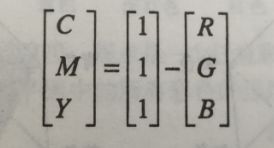
青色不反射红光、深红色不反射绿色、纯黄色不反射蓝色
CMYK是在青色、深红色、纯黄色基础上再加上黑色;
6.1.3、HSI彩色模型
RGB和CMY是适应于系统的颜色模型;而HSI模型是针对人解释的颜色;
当人观察一个彩色物体时,通常用色调、饱和度、亮度来描述
HSI彩色模型由 色调、饱和度、亮度作为基础描述;
色调是描述一种纯色的颜色属性;
饱和度是描述一种纯色被白光稀释的程度的度量。
亮度是一个主观的描述子,实际上无法度量,体现了无色的强度概念,是描述彩色感觉的关键因素之一。
HSI对于颜色描述是最理想的; RGB对图像颜色生成是最理想的。

HSI空间是由一个垂直强度轴(黑色到白色)和位于该强度轴垂直平面内的彩色点的轨迹表示,当平面沿着强度轴上下移动时,由每个平面与立方体表面构成的横截面定义的边界不是三角形就是六边形。
三原色是按照120°排列,二次色和原色相差60°,故二次色之间也相差120°;
*
色调是由来自某参考点的角度决定,通常,与红轴角度为0的称为0色调,从此开始,色调逆时针方向增长;
饱和度(距垂直轴间的距离)是从原点到该点的向量长度;
强度由垂直轴上的平面的位置给出;
HSI空间的重要分量是垂直强度轴、到一个彩色点的向量长度和该向量与红轴的夹角。

2、HSI和RGB之间的转换
给定一副RGB彩色格式的图像,每个RGB像素的H分量可用下式得到:
从RGB转化到HSI:


饱和度分量:

强度分量:

从HSI转换到RGB:

代码实现:.
RGB空间转换为HSI空间:
#include HSI空间转换为HSI空间:
//hsi转变为rgb空间
Mat HSI2BGR(const Mat & hsi)
{
Mat rgb(hsi.rows, hsi.cols, hsi.type());
float B, G, R = 0;
for (int i = 0; i < hsi.rows; i++)
{
for (int j = 0; j < hsi.cols; j++)
{
float H = hsi.at<Vec3b>(i, j)[0] / 255.f * 2 * MY_PI, //除以2Π是将角度转化为弧度
S = hsi.at<Vec3b>(i, j)[1] / 255.f ,
I = hsi.at<Vec3b>(i, j)[2] / 255.f ;
if (H < 120.f * MY_PI / 180.f) //角度转化为弧度
{
B = I * (1 - S);
R = I * (1 + S * cos(H) / cos(60.f* MY_PI / 180.f - H));
G = 3 * I - R - B;
}
else if (H >= 120.f * MY_PI / 180.f && H < 240 * MY_PI / 180.f)
{
H -= (120.f * MY_PI / 180.f);
R = I * (1 - S);
G = I * (1 + S * cos(H) / cos(60.f* MY_PI / 180.f - H));
B = 3 * I - R - G;
}
else if (H >= 240.f * MY_PI / 180.f)
{
H -= (240.f * MY_PI / 180.f);
G = I * (1 - S);
B = I * (1 + S * cos(H) / cos(60.f* MY_PI / 180.f - H));
R = 3 * I - B - G;
}
rgb.at<Vec3b>(i, j)[0] = B * 255;
rgb.at<Vec3b>(i, j)[1] = G * 255;
rgb.at<Vec3b>(i, j)[2] = R * 255;
}
}
return rgb;
}
int main()
{
Mat img = imread("C:/Users/征途/Desktop/vs-cpp/第六章/02.jpg");
if (!img.data)
{
cout << "错误" << endl;
}
imshow("img", img);
Mat dst1,dst2;
dst1 = RGB2HSI(img);
//imshow("dst1", dst1);
dst2 = HSI2BGR(img);
imshow("dst2", dst2);
waitKey(0);
return 0;
}
6.2伪彩色图像处理
伪彩色处理是基于一种指定的规则对灰度值赋以颜色的处理。
术语伪彩色用于区分对单色图像赋予真彩色图像处理;
伪彩色处理的应用是人目视观察和解释单幅图像或序列图像中的灰度级事件;
伪彩色处理主要分为: 灰度分层、彩色编码
6.2.1、灰度分层
伪彩色图像处理也叫假彩色图像处理,根据一定的准则对灰度值赋以彩色的处理。
灰度级分层通常用于突出感兴趣的特定灰度范围内的亮度。灰度级分层有两大基本方法。
将感兴趣的灰度范围内的值显示为一个值(比如0),而其他范围的值为另外一个值(255)。
将感兴趣的灰度范围内的值显示为一个值(比如0),而其他范围的值不变。
灰度分层(密度分层)就是将一幅图像描述为三维函数:则分层方法可以看为房置一些平行于该图像的坐标平面的平面,然后,每个平面在相交的区域中“切割”图像函数。如下图所示,使用了位于f(x,y)=l,处的一个平面将把该图像函数切割为两部分的一个例子。

对上述图片的平面的每一赋予不同的颜色,平面上面的任何灰度级的像素将编码成一种彩色,该平面之下的任何像素将编码为另一种颜色。
位于平面上的灰度级被任意赋予不同的两种彩色之一,结果是一副只有两种颜色的图像;
该技术总结为:
令【0,L-1】表示灰度级,令l0表示黑色(f(x,y)=0 ),并且令L-1表示白色(f(x,y)= L-1);假定垂直于灰度轴在P个平面定义为灰度级l0,l1–lp;假定0< P
其中ck是第K个灰度区间Vk有关在颜色,Vk由位于l=k-1和l = k处分割平面定义;
平面的概念:
根据映射函数可以知道,任何输入的灰度级根据其是位于Li值的上面还是下面而赋予两种颜色之一。
当用更多的灰度级函数时,映射函数采用一种阶梯形式。

6.2.2彩色编码
彩色编码是对任何输入的像素的灰度值采用3个独立的变换,然后,将3个变化结果分别送人彩色电视检测器的红绿蓝通道,产生了一幅合成图像,该合成图像的彩色内容是变换函数的彩色特性来调制的。这种方法是对一副图像的灰度值进行变换,而不是位置函数。
灰度级线性函数用来产生颜色

下图是对灰度图像伪彩色化的区域划分:属于灰度分层,然后三个通道逐次赋值,然后合并通道:
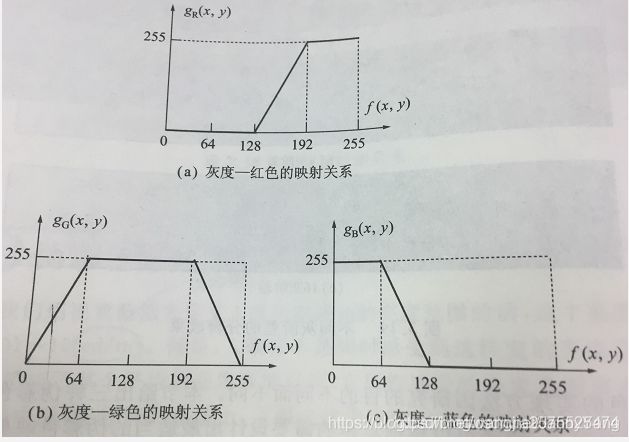
代码实现:
#include OpenCV自带函数applycolormap(伪彩色函数)
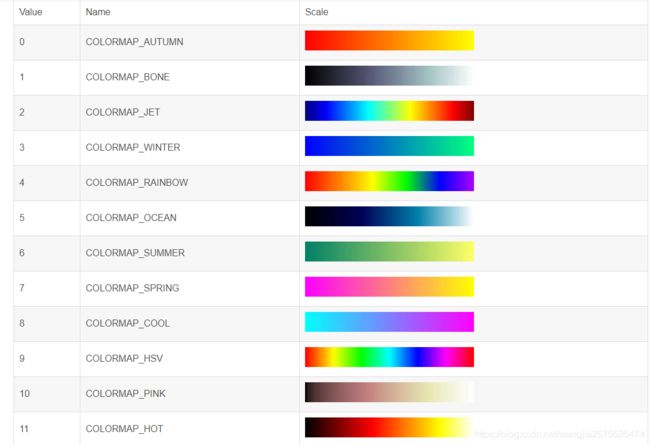
OpenCV的定义12种colormap(色度图),可以应用于灰度图像,使用函数applycolormap产生伪彩色图像。让我们很快看到如何将色度图的一种模式colormap_jet应用到一幅图像中。
using namespace cv;
Mat im_gray = imread( "pluto.jpg" , IMREAD_GRAYSCALE);
Mat im_color;
applyColorMap(im_gray, im_color, COLORMAP_JET);
下图显示了一个关于colormap(色度图)的视觉表示和COLORMAP_*的数值,左边的颜色模式表示较低的灰度值,右边的则表示较高的灰度值。
6.3全彩色图像处理基础
全彩色图像处理分为两大类:
第一类,分别处理每一副分量图像,然后由分别处理过的分量图像来形成一副处理过的合成彩色图像;
第二类,直接处理彩色图像。
全彩色图像至少有3个分量,所以彩色像素实际上是向量;
例如,在一个RGB系统中,每个彩色点可以用RGB坐标系统中从原点延伸到该点的一个向量来解释。
令c表示RGB中一个任意的分量:
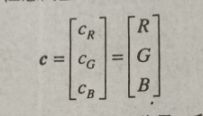
可以认为彩色分量是关于xy的函数:
.
对于M*N大小的图像,就有MN个这样的向量c(x,y)其中x=0,1,2…M-1; y=0,1,2…N-1;
为了使得每种彩色分量处理和基于向量的处理相等,必须满足两个条件:
第一,处理必须对向量和标量都可用;
第二,对向量的每一分量的操作对于其他分量必须是独立的;
6.3.1、分离彩色通道函数:
**Vector channels;
split(srcimage, channels);
Mat img blue channels = channels.at(0);
Mat img green channels = channels.at(1);
Mat img red channels = channels.at(2);
**
6.3.3、访问彩色通道函数:
image.at(i,j)[0];
image.at(i,j)[1];
image.at(i,j)[2];
6.3.3、合并彩色通道函数:
merge(输入要被合并的矩阵,输入矩阵个数通道数,输出)
merge(img, 3, dst )
6.4彩色图像处理
3.1 彩色变换
彩色变换主要涉及在单一色彩模型内处理彩色图像的分量,而不是这些分量在不同模型间的转换。
![]()
![]()
主要思路还是将彩色图像的各分量分开,以灰度图像处理的方式分别处理。
- 补色;
- 彩色分层;
- 色调和彩色矫正;
- 直方图处理;
- 平滑和锐化;
- 基于彩色的图像分割。
3.2 平滑和锐化
平滑:
3.3 基于彩色的图像分割
HSI彩色空间分割;
RGB向量空间分割;
彩色边缘检测。