深度学习基础（3）——神经网络与常用函数

概述

在我们学习深度学习模型，或者了解某种算法的过程中，经常会看到如卷积层，全连接层，归一化，正则化，激活函数等概念，这些东西如果直接看的话十分的多且杂乱，在此对其进行梳理。

神经网络简介

神经网络是深度学习中最常见也是最基础的概念，神经网路的基础组成单元为神经元，神经网络的通常包括：输入层，隐含层，输出层。以下对一些神经网络做一个简介。

感知器（Perceptron）

第一代神经网络就是感知器（Perceptron）。感知器是一个二分类线性分类模型，其输入为实例的特征向量，输出为实例的类别。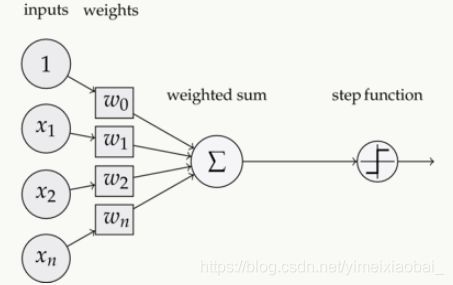
（上图为一个单层感知器）
图中输入向量为x，权重向量为w，w0为偏置。可以看到它只是将输入进行线性的计算再输出1或者-1，也就是判断其正确与否。可以看成一个简单的二元线性分类器。

多层感知器（MLP）

多层感知器就是含有至少一个隐藏层的由全连接层组成的神经网络，且每个隐藏层的输出通过激活函数进行变换，多层感知机的层数个各个隐藏层中隐藏单元个数都是超参数，多层感知器的提出解决了异或问题，实现非线性分类。

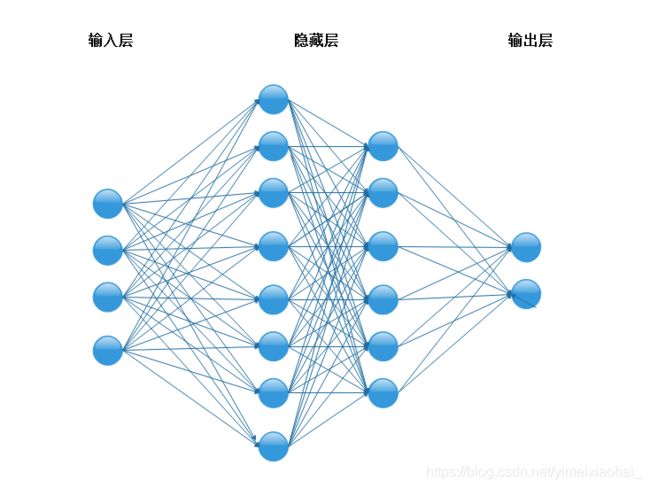
提到多层感知器就离不开两个概念：反向传播和激活函数。
反向传播算法可以参考李宏毅老师的详解：
http://speech.ee.ntu.edu.tw/~tlkagk/courses_MLSD15_2.html
激活函数则是在隐藏层中使用，将线性组合得到的结果进行处理，得到一个非线性的值。在函数中会详细介绍

卷积神经网络（CNN）

卷积神经网络是一种用来处理局部和整体相关性的计算网络结构，因为图像数据具有显著的局部与整体关系，CNN多用于对图像的处理。一般来说CNN包括输入层，卷积层，池化层，全连接层。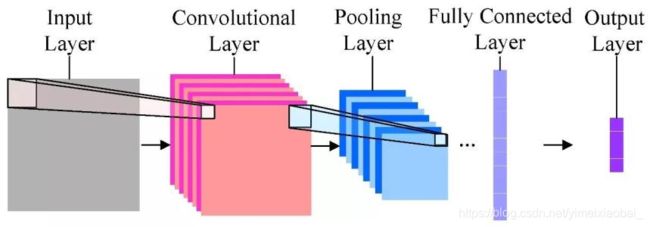
输入层：通常三维彩色图像，以图像分类任务为例，输入层输入的图像一般包含RGB三个通道，是一个由长宽分别为$H$和$W$组成的3维像素值矩阵$H\times W\times 3$，根据计算能力、存储大小和模型结构的不同，卷积神经网络每次可以批量处理的图像个数不尽相同，若指定输入层接收到的图像个数为$N$，则输入层的输出数据为$N\times H\times W\times 3$。

卷积层：通常用作对输入层输入数据进行特征提取，数学原理是对两张像素矩阵进行点乘求和的数学操作，其中一个矩阵为输入的数据矩阵，另一个矩阵则为卷积核（滤波器或特征矩阵），求得的结果表示为原始图像中提取的特定局部特征。

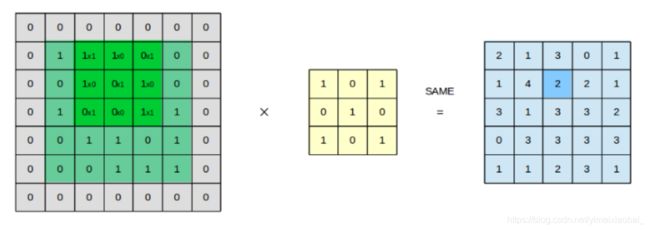
池化层：池化层又称为降采样层(Downsampling Layer)，作用是对感受域内的特征进行筛选，提取区域内最具代表性的特征，能够有效地降低输出特征尺度，进而减少模型所需要的参数量。按操作类型通常分为最大池化(Max Pooling)、平均池化(Average Pooling)和求和池化(Sum Pooling)，它们分别提取感受域内最大、平均与总和的特征值作为输出，最常用的是最大池化。

全连接层：全连接层(Full Connected Layer)负责对卷积神经网络学习提取到的特征进行汇总，将多维的特征输入映射为二维的特征输出。

通常来说不同层次的卷积操作提取到的特征类型是不相同的，在具体的设计过程中可根据需求来设计卷积神经网络。

循环神经网络（RNN）

CNN多用于处理图像这类具有显著的局部与整体关系的数据，但是现实生活有很多数据属于时间序列数据，即在不同时间点上收集到的数据，这类数据反映了某一事物、现象等随时间的变化状态或程度。比如：当文本与视频单独的看一个文字或者一帧图像，都无法理解它们的意思，需要对它们连起来的这个序列进行分析，才能准确理解其含义。为了解决一些这样类似的问题，能够更好的处理序列的信息，RNN就由此诞生了。

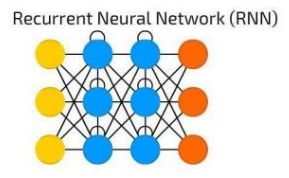
与CNN相比，RNN的结构比较简单, 它主要有输入层,隐藏层, 输出层组成。
对于之前提到的普通神经网络难以处理的时序数据，RNN引入了隐状态$h$（hidden state），$h$可对序列数据提取特征，接着再转换为输出。


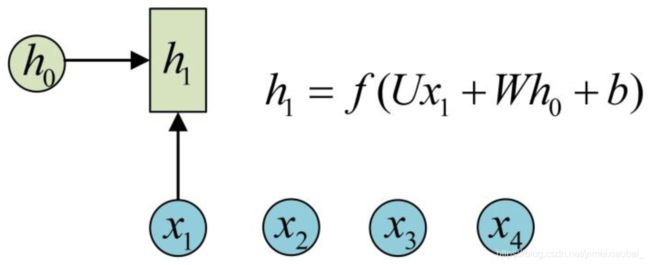
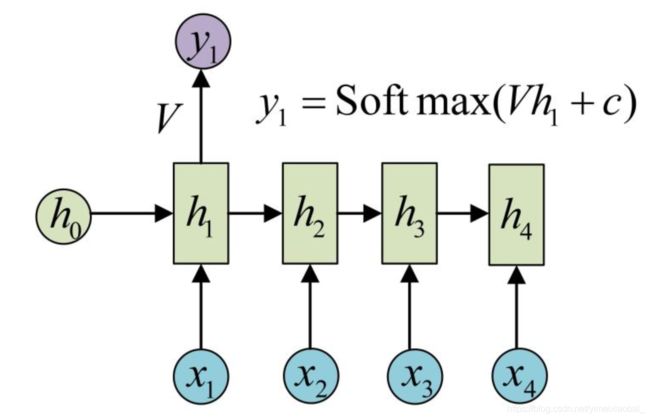
其中$X$为向量，$y$为输出，$h$为隐状态。这就是最经典的RNN结构

生成对抗式网络（GAN）

作为近年来的热门项目，GAN在不少邻域都取得了不错的效果，GAN由生成器和判别器组成，生成器负责生成样本，判别器负责判断生成器生成的样本是否为真。生成器要尽可能迷惑判别器，而判别器要尽可能区分生成器生成的样本和真实样本。我们可以通俗的把它表示如下：

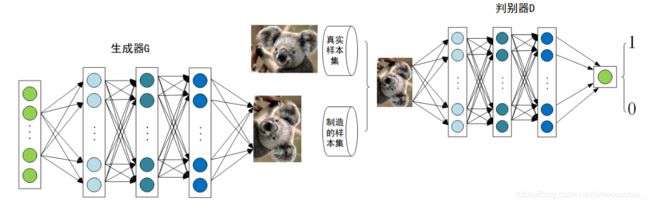
上述模型左边是生成器G，其输入是$z$，对于原始的GAN，$z$是由高斯分布随机采样得到的噪声。噪声$z$通过生成器得到了生成的假样本。生成的假样本与真实样本放到一起，被随机抽取送入到判别器D，由判别器去区分输入的样本是生成的假样本还是真实的样本。整个过程简单明了，生成对抗网络中的“生成对抗”主要体现在生成器和判别器之间的对抗。

以上就是一些常用的神经网络的简介，具体的详解可以参考博客。

常用函数与术语

深度学习模型的设计和优化中使用到了各式各样的方法，在此对一些常见的术语和函数做一个介绍。

激活函数

激活函数的意义在于讲神经网络中简单的线性组合非线性化，非线性激活函数能够使神经网络逼近任意复杂的函数。如果没有激活函数引入的非线性，多层神经网络就相当于单层的神经网络。以下对常用的激活函数进行一个简介，不做详细解释：
Sigmoid激活函数：Sigmoid函数的作用将是一个实数值压缩到0至1的范围内。在数学上表示为：

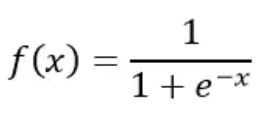
Sigmoid函数作为初期的一个经典函数曾经被广泛的使用，但是随着深度学习的发展它的问题也暴露出来，梯度消失，非零中心，消耗大等。于是有更多新的激活函数的出现。

Tanh激活函数：Tanh也被称为双曲正切激活函数。类似sigmoid，它的作用也是把一个实数值压缩。与sigmoid不同的是，tanh在-1到1的输出范围内是零均值的。公式如下：


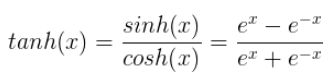
Tanh函数的出现解决了sigmoid函数输出不是以零为中心的问题，但是没有解决函数过饱和后梯度消失和消耗过大的问题。

ReLU激活函数：ReLU也被称为修正线性函数。它能保证输出值为非负数，公式如下：

ReLU的出现至少在正区间解决了梯度消失的问题，而且从形式上看它只有线性关系，不需要指数计算，计算速度都比sigmoid和tanh都要快。但是它的输出也不是以零为中心且随着训练的进行，可能会出现神经元死亡，权重无法更新的情况。

Leaky ReLU激活函数：Leaky ReLU与ReLU不同的是，在负区间它并不是直接讲函数值设为零，而是增加了一个超参数，避免出现神经元死亡的情况：

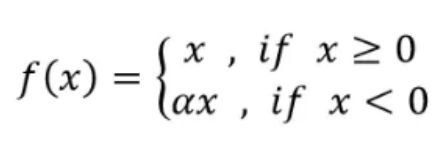
它解决了训练过程中神经元死亡的问题，但是超参数需要先验知识的支持。

PReLU激活函数：PReLU也被称为带参数的修正线性函数。它的思想是引进任意超参数，而这个可以通过反向传播学习（leaky relu中的超参数是人为设定的）。公式如下：

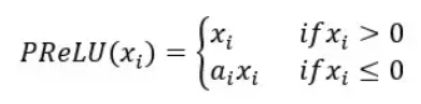
神经元在负区间内自动选择最好的斜率，它可以变成单纯的ReLU激活函数或者Leaky ReLU激活函数。

不同的激活函数的功能不同，在设计激活函数的时候应该根据具体需求来进行分析设计。

损失函数

损失函数（Loss Function）又叫做误差函数，用来衡量算法的运行情况，估量模型的预测值与真实值的不一致程度，是一个非负实值函数，通常使用
L(Y, f(x))来表示。损失函数越小，模型的鲁棒性就越好。损失函数是经验风险函数的核心部分，也是结构风险函数重要组成部分。常用的损失函数有：
0-1损失函数
如果预测值和目标值相等，值为0，如果不相等，值为1。

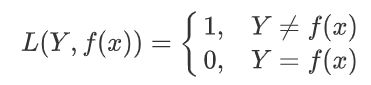
绝对值损失函数

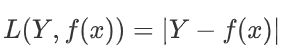
平方损失函数

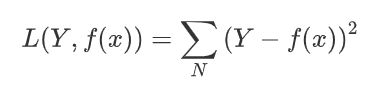
对数损失函数

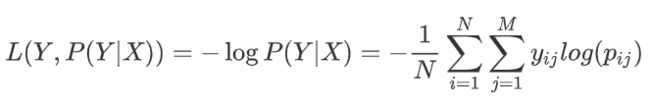
其中, Y 为输出值, X为输入值 L 为损失函数. N为输入样本总数, M为可能的类别数, $y_{ij}$ 是一个二值指标, 表示类别 j 是否是输入实例 xi 的真实类别. $p_{ij}$ 为模型或分类器预测输入实例 xi 属于类别 j 的概率.

指数损失函数

Hinge损失函数

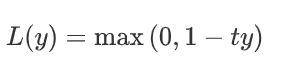
其中y是预测值，范围为(-1,1)，t为目标值，其为-1或1。

在了解损失函数的同时我们要注意几个概念；通常损失函数的概念出现最多，但是如果要细分的话可按照以下定义进行理解。
损失函数：主要指单个样本的损失或误差；
代价函数：输入模型的全部样本的评价误差。
目标函数：相当于代价函数 + 正则化项

在实际的应用中，并不是损失函数越小，就代表模型拟合的越好。还有一个概念叫风险函数(risk function)。风险函数是损失函数的期望，这是由于输入输出的(X,Y)遵循一个联合分布，但是这个联合分布是未知的，所以无法计算。但是可以根据训练集，f(X)关于训练集的平均损失称作经验风险(empirical risk)，公式如下：

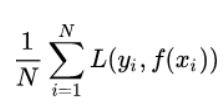
但是如果过度学习训练集，导致它在真正预测时效果会很不好，这种情况称为过拟合(over-fitting)。不仅要让经验风险最小化，还要让结构风险最小化。所以定义了一个函数J(f)，这个函数专门用来度量模型的复杂度，在机器学习中也叫正则化(regularization)。常用的有L1， L2范数。最终的优化函数为：

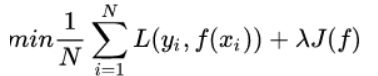
梯度下降

在上文提到神经网络根据代价函数来实现对参数的更新，在此介绍一种最常见的优化算法：梯度下降，梯度下降法有以下几个作用：

• 梯度下降是迭代法的一种，可以用于求解最小二乘问题。
• 在求解机器学习算法的模型参数，即无约束优化问题时，主要有梯度下降法（Gradient Descent）和最小二乘法。
• 在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。
• 如果我们需要求解损失函数的最大值，可通过梯度上升法来迭代。梯度下降法和梯度上升法可相互转换。

梯度下降法算法步骤如下：
（1）确定优化模型的假设函数及损失函数。假设函数为：

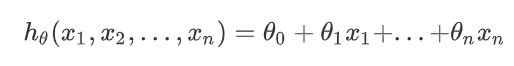
其中，${\theta }_i,x_i(i=0,1,2,...,n)$分别为模型参数、每个样本的特征值。
损失函数为：

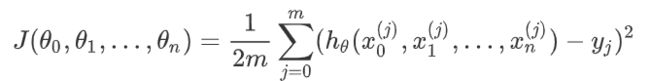
（2）参数初始化
主要初始化参数、算法迭代步长、终止距离。初始化时可以根据经验初始化。也可选择随机初始化。

（3）迭代计算。
计算当前位置时损失函数的梯度，对${\theta }_i,$，其梯度表示为：

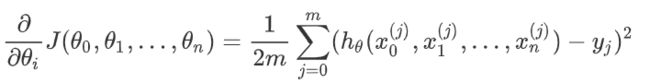
计算当前位置下降的距离；

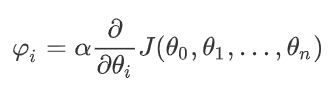
判断是否终止；
更新所有的${\theta }_i$，再重复步骤。