朴素贝叶斯、精确率与召回率、交叉验证
朴素贝叶斯、精确率与召回率、交叉验证
一、朴素贝叶斯
(1)朴素贝叶斯的原理
(2)朴素贝叶斯公式的使用
二、朴素贝叶斯API
(1)朴素贝叶斯案例
(2)朴素贝叶斯总结
三、分类模型的评估
(1)混淆矩阵
(2)精确率(Precision)与召回率(Recall)
(3)F1分数
(4)分类模型评估的API
四、交叉验证与网格搜索
(1)验证集
(2)交叉验证
(3)交叉验证与超参数选择
(4)超参数的网格化搜索
(5)交叉验证和网格化搜索的API
朴素贝叶斯
(1)朴素贝叶斯的原理
什么是朴素贝叶斯:贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。而朴素朴素贝叶斯分类是贝叶斯分类中最简单,也是常见的一种分类方法。
贝叶斯公式:
P ( Y ∣ X ) = P ( X ∣ Y ) P ( Y ) P ( X ) P(Y|X)=\frac{P(X|Y)P(Y)}{P(X)} P(Y∣X)=P(X)P(X∣Y)P(Y)
X:特征向量 Y:类别
**先验概率 **P(X)P(X) :先验概率:是指根据以往经验和分析得到的概率。
后验概率P(Y|X)P(Y|X):事情已经发生,要求这件事情发生的原因是由某个因素引起的可能性的大小。
类条件概率P(X|Y)P(X|Y):在已知某类别的特征空间中,出现特征值X的概率密度。
朴素:朴素贝叶斯算法是假设各个特征之间相互独立,也是朴素这词的意思。那么贝叶斯公式中P(X|Y)可写成
P ( X ∣ Y ) = P ( x 1 ∣ Y ) P ( x 2 ∣ Y ) ⋯ P ( x n ∣ Y ) P(X|Y)=P(x_{1}|Y)P(x_{2}|Y)⋯P(x_{n}|Y) P(X∣Y)=P(x1∣Y)P(x2∣Y)⋯P(xn∣Y)
朴素贝叶斯公式:
P ( Y ∣ X ) = P ( x 1 ∣ Y ) P ( x 2 ∣ Y ) ⋯ P ( x n ∣ Y ) P ( Y ) P ( X ) P(Y|X)=\frac{P(x_{1}|Y)P(x_{2}|Y)⋯P(x_{n}|Y)P(Y)}{P(X)} P(Y∣X)=P(X)P(x1∣Y)P(x2∣Y)⋯P(xn∣Y)P(Y)
另外三种常见模型
- 多项式模型:多项式模型在计算先验概率
P(Yk)和条件概率P(xi|Yk)时,会做一些平滑处理,具体公式为:
P ( Y k ) = N Y k + α N + K α P(Y_{k})=\frac{N_{Y_{k}}+\alpha}{N+K\alpha} P(Yk)=N+KαNYk+α
-
高斯模型
当特征是连续变量的时候,假设特征分布为正太分布,根据样本算出均值和方差,再求得概率。
P ( x i ∣ y ) = 1 2 π σ y 2 e x p ( − ( x i − μ y ) 2 2 σ y 2 ) P(x_{i}|y)=\frac{1}{\sqrt{2\pi\sigma^2_{y}}}exp(-\frac{(x_{i}-\mu_{y})^2}{2\sigma^2_{y}}) P(xi∣y)=2πσy21exp(−2σy2(xi−μy)2) -
伯努利模型
伯努利模型适用于离散特征的情况,伯努利模型中每个特征的取值只能是1和0。
P ( x i ∣ y ) = P ( i ∣ y ) x i + ( 1 − P i ∣ y ) ( 1 − x i ) P(x_{i}|y)=P(i|y)x_{i}+(1-P{i|y})(1-x_{i}) P(xi∣y)=P(i∣y)xi+(1−Pi∣y)(1−xi)
(2)朴素贝叶斯公式的使用
我们结合一个例子来分析贝叶斯公式的使用。
假如训练集中,有两类文档,一类是科技,另一类是娱乐,两类文档各有10篇。这两类文档中部分词汇出现的次数如下:
现有一篇文档,出现了“影院”、“支付宝”、“云计算”等词汇,分别计算其属于科技、娱乐的概率
如果把科技、娱乐分别设为事件A1和A2,“商场”、“影院”、“支付宝”、“云计算”分别设为事件B1,B2,B3,B4。
那么问题就相当于求P(A1|(B2,B3,B4))和P(A2|(B2,B3,B4))
根据贝叶斯公式,有:
P ( A 1 ∣ ( B 2 , B 3 , B 4 ) ) = P ( ( B 2 , B 3 , B 4 ) ∣ A 1 ) P ( A 1 ) P ( B 2 , B 3 , B 4 ) P(A1|(B2,B3,B4))=\frac{P((B2,B3,B4)|A1)P(A1)}{P(B2,B3,B4)} P(A1∣(B2,B3,B4))=P(B2,B3,B4)P((B2,B3,B4)∣A1)P(A1)
这里假设B2,B3,B4这三个事件相互独立,那么有:
P ( B 2 , B 3 , B 4 ) = P ( B 2 ) P ( B 3 ) P ( B 4 ) P ( ( B 2 , B 3 , B 4 ) ∣ A 1 ) P ( A 1 ) = P ( B 2 ∣ A 1 ) P ( B 3 ∣ A 1 ) P ( B 4 ∣ A 1 ) P(B2,B3,B4)=P(B2)P(B3)P(B4)\\ {P((B2,B3,B4)|A1)P(A1)}=P(B2|A1)P(B3|A1)P(B4|A1) P(B2,B3,B4)=P(B2)P(B3)P(B4)P((B2,B3,B4)∣A1)P(A1)=P(B2∣A1)P(B3∣A1)P(B4∣A1)

同理:
P ( A 2 ∣ ( B 2. B 3 , B 4 ) ) = P ( ( B 2. B 3 , B 4 ) ∣ A 2 ) P ( A 2 ) P ( B 2 , B 3 , B 4 ) P(A2|(B2.B3,B4))=\frac{P((B2.B3,B4)|A2)P(A2)}{P(B2,B3,B4)} P(A2∣(B2.B3,B4))=P(B2,B3,B4)P((B2.B3,B4)∣A2)P(A2)

上面出现了概率等于0,这有点极端,这篇文章也出现了“商场”,不能因为“云计算”这个词在训练集的娱乐类文章中没有出现,就判定其为娱乐文章的概率为0。如果词频列表里面有很多出现次数都为0,很可能计算结果都为零。
为了处理这种极端情况,这里引入一个拉普拉斯平滑系数:
在这个例子中,α为1,m为4,那么计算P(A2|(B2,B3,B4))结果为:
如果P(A2|(B2,B3,B4))加了,计算P(A1|(B2,B3,B4))也要加:
按理说,P(A1|(B2,B3,B4))与P(A2|(B2,B3,B4))之和,应该为1,即便加入拉普拉斯算子,概率和也应该在1左右,但计算结果并非如此,原因是B2,B3,B4不满足独立性假设,即下面的两个公式不成立:
P ( B 2 , B 3 , B 4 ) = P ( B 2 ) P ( B 3 ) P ( B 4 ) P ( ( B 2 , B 3 , B 4 ) ∣ A 1 ) = P ( B 2 ∣ A 1 ) P ( B 3 ∣ A 1 ) P ( B 4 ∣ A 1 ) P(B2,B3,B4)=P(B2)P(B3)P(B4)\\ P((B2,B3,B4)|A1)=P(B2|A1)P(B3|A1)P(B4|A1) P(B2,B3,B4)=P(B2)P(B3)P(B4)P((B2,B3,B4)∣A1)=P(B2∣A1)P(B3∣A1)P(B4∣A1)
这个例子仅仅是为了介绍朴素贝叶斯公式的应用,给出的数据有一些不合理的地方。
2、朴素贝叶斯API
使用sklearn.naive_bayes.MultinomialNB类
sklearn.naive_bayes.MultinomialNB(alpha = 1.0) #朴素贝叶斯分类
alpha:拉普拉斯平滑系数
(1)朴素贝叶斯案例
使用20类新闻数据做文本分类:
1、加载20类新闻数据,并进行分割
2、生成文章特征词
3、朴素贝叶斯estimator流程进行预估
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
# 下载数据
news = fetch_20newsgroups(subset='all')
# 进行数据分割
x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.25)
# 对数据集进行特征抽取,使用tf-idf
tf = TfidfVectorizer()
# 以训练集中出现的词,进行重要性统计
x_train = tf.fit_transform(x_train)
# 对于在训练集出现的词,计算它们在测试集中的tf-idf
x_test = tf.transform(x_test)
# 假如训练集经特征抽取后的词为['a','b','c','d']
# 那么测试集也只统计['a','b','c','d'],对于测试集中出现的其他词,这里不做tf-idf统计
# 这样可以保证训练集和测试集的特征数量一致
# 但是,在算词频(tf)和逆文本率(idf)的时候,是在测试集内部统计词频和你文本率
# 进行朴素贝叶斯算法的预测
# 初始化一个朴素贝叶斯工具
mlt = MultinomialNB(alpha=1.0)
# 将训练数据代入
mlt.fit(x_train, y_train)
# 将测试数据代入
y_predict = mlt.predict(x_test)
print("预测的文章类别为:", y_predict)
# 得出准确率
print("准确率为:", mlt.score(x_test, y_test))
输出
预测的文章类别为: [ 8 10 19 ... 14 15 16]
准确率为: 0.8482597623089984
训练集即为已知数据,测试集为未知数据。
上面的程序中,在将训练数据代入的那一步(mlt.fit(x_train, y_train)),就是计算各种先验概率和条件概率,做predict的时候,基本就是直接套贝叶斯公式了。
sklearn实战
使用的是sklearn.naive_bayes中的高斯模型,数据为约会数据(是连续的),数据和代码可前往:
https://github.com/AugusXJ/scikit_learn/tree/master/Bayes
from sklearn import metrics
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
# 读取数据
X = []
Y = []
fr = open("datingTestSet.txt")
index = 0
for line in fr.readlines():
line = line.strip()
line = line.split('\t')
X.append(line[:3])
Y.append(line[-1])
#归一化
scaler = MinMaxScaler()
X = scaler.fit_transform(X)
# 交叉分类
train_X,test_X, train_y, test_y = train_test_split(X,
Y,
test_size=0.2) # test_size:测试集比例20%
# KNN模型,选择3个邻居
model = GaussianNB()
model.fit(train_X, train_y)
print(model)
expected = test_y
predicted = model.predict(test_X)
print(metrics.classification_report(expected, predicted)) # 输出分类信息
label = list(set(Y)) # 去重复,得到标签类别
print(metrics.confusion_matrix(expected, predicted, labels=label)) # 输出混淆矩阵信息
(2)朴素贝叶斯总结
优点:
朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率;
朴素贝叶斯不需要调参,拉普拉斯平滑系数,不算参数;
对缺失数据不太敏感(少一个词,少一个句子对分类结果影响不大),算法也比较简单,常用于文本分类。
分类准确度高,速度快
缺点:
需要知道先验概率P(F1,F2,…|C),而这个概率需要假设F1,F2,……相互独立才能算出来,因此在某些时候会由于相互独立的假设不成立导致预测效果不佳,比如前面说的各个词的独立性假设不成立。
3、分类模型的评估
之前我们一直在使用准确率来评估模型,但具体的应用场景中,准确率并不是唯一的度量,也未必是最佳的度量标准。这里介绍一下精确率和召回率。
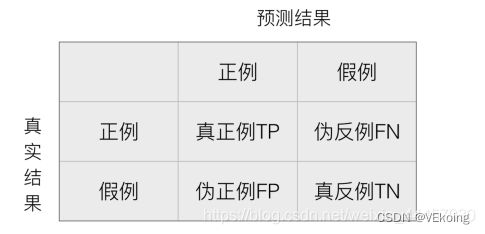
(1)混淆矩阵
在分类任务下,预测结果(Predicted Condition)与真实结果(True Condition)之间存在四种不同的组合,构成混淆矩阵(适用于多分类)
比如,一个为正的结果,被算法认定为负,这就伪反例。
对于数据中的每一个分类,都有一个混淆矩阵。
(2)精确率(Precision)与召回率(Recall)
精确率:预测结果为正例样本中,真实为正例的比例(查得准)
召回率:真实为正例的样本中预测结果为正例的比例(查的全,对正样本的区分能力)
(3)F1分数
在一些应用场景中,需要比较高的召回率,比如癌症检测当中,需要查的全,所以允许一定范围内的错检,但一味地提高召回率,经常容易造成精确率的下降,因此需要一个兼顾精确率和召回率的指标。
F1分数就是综合了精确率和召回率的评判指标,其计算公式如下:
F 1 = 2 T P 2 T P + F N + F P = 2 ⋅ P r e c i s i o n ⋅ R e c a l l P r e c i s i o n + R e c a l l F1=\frac{2TP}{2TP+FN+FP}=\frac{2\cdot Precision \cdot Recall}{Precision + Recall} F1=2TP+FN+FP2TP=Precision+Recall2⋅Precision⋅Recall
(4)分类模型评估的API
输入数据的真实值和预测值
sklearn.metrics.classification_report(y_true, y_pred, target_names=None)
y_true:真实目标值
y_pred:估计器预测目标值
target_names:目标类别名称,即类别标签名称
return:每个类别精确率与召回率
对前面的朴素贝叶斯模型进行评估,只需要在最后面加上一句评估的代码,完整代码如下:
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import classification_report
# 下载数据
news = fetch_20newsgroups(subset='all')
# 进行数据分割
x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.25)
# 对数据集进行特征抽取,使用tf-idf
tf = TfidfVectorizer()
# 以训练集中出现的词,进行重要性统计
x_train = tf.fit_transform(x_train)
# 对于在训练集出现的词,计算它们在测试集中的tf-idf
x_test = tf.transform(x_test)
# 进行朴素贝叶斯算法的预测
# 初始化一个朴素贝叶斯工具
mlt = MultinomialNB(alpha=1.0)
# 将训练数据代入
mlt.fit(x_train, y_train)
# 将测试数据代入
y_predict = mlt.predict(x_test)
print("预测的文章类别为:", y_predict)
# 得出准确率
print("准确率为:", mlt.score(x_test, y_test))
# 得出精确率和召回率
print("每个类别的精确率和召回率:")
print(classification_report(y_test, y_predict, target_names=news.target_names))
输出
预测的文章类别为: [ 0 15 4 ... 8 12 17]
准确率为: 0.8414685908319185
每个类别的精确率和召回率:
precision recall f1-score support
alt.atheism 0.85 0.68 0.76 212
comp.graphics 0.88 0.77 0.82 254
comp.os.ms-windows.misc 0.88 0.79 0.83 260
comp.sys.ibm.pc.hardware 0.76 0.84 0.80 259
comp.sys.mac.hardware 0.85 0.87 0.86 227
comp.windows.x 0.91 0.89 0.90 223
misc.forsale 0.90 0.70 0.78 245
rec.autos 0.89 0.90 0.90 251
rec.motorcycles 0.95 0.96 0.96 244
rec.sport.baseball 0.95 0.94 0.95 240
rec.sport.hockey 0.92 0.98 0.95 243
sci.crypt 0.81 0.98 0.89 264
sci.electronics 0.89 0.75 0.82 259
sci.med 0.97 0.90 0.93 244
sci.space 0.87 0.96 0.91 224
soc.religion.christian 0.50 0.97 0.66 238
talk.politics.guns 0.72 0.95 0.82 228
talk.politics.mideast 0.94 0.97 0.95 233
talk.politics.misc 1.00 0.60 0.75 199
talk.religion.misc 0.96 0.16 0.28 165
accuracy 0.84 4712
macro avg 0.87 0.83 0.83 4712
weighted avg 0.87 0.84 0.84 4712
最后一列support,指的是将文章划分为相应类别的数量,比如第一行的support是212,意思测试集的样本中,被划到alt.atheism类的数量有212。
如果在classification_report中不加入目标值名称,那么输出的结果中,将没有类名名称
4 交叉验证与网格化搜索
(1)验证集
假如算法工程师手里只有训练集,没有测试集,测试集在客户手里,算法工程师把模型训练出来之后提交给客户,客户使用测试集对模型进行测试,测试合格支付尾款。
在上面的场景中,算法工程师面对训练出来的模型,他怎么知道模型是否会过拟合于训练集?(所谓过拟合,指的是在训练集效果好,但在测试集上效果差)
一个很好的办法是从训练集中划出一部分数据出来测试模型,以替代测试集的功能,这部分数据就叫做验证集。
如果模型在验证集上的表现不好,那就回去调整模型参数,重新训练,然后放到验证集上查看效果,因此验证集上的数据是参与了调参的。
(2)交叉验证
若本身样本数量不多,从训练集中分出一个验证集,那么训练数据就会变少,模型的训练效果将会受到影响,此外,某些异常样本也可能被划入验证集,导致模型表现异常。
为了解决由于样本数量少导致的上述问题,可以使用交叉验证,其过程如下:
将训练集N等分,每次取其中一份为验证集,剩下N-1份为新的训练集,然后把训练集上得出来的模型,放到验证集上,得出一个准确率,接着把剩下N-1份的训练集,轮流作为验证集,重复同样的工作。将每次得到的模型,都放在验证集上,分别得到一个准确率,取平均值,就是当前超参数组合训练出来的模型,在训练集+验证集上准确率(例如4折交叉验证,每轮训练得到一个模型后,放在验证集上获得准确率并将其保存,四轮结束之后,可以得到4个准确率,对这四个准确率取平均值,就是最后的准确率)。
上述过程就叫称为交叉验证(cross validation,简称CV),把数据N等分,就是N折交叉验证,其中10折交叉验证最为常用。
这里演示一下四折交叉验证的示意图:

交叉验证使得每一个样本都有一次机会成为验证集,使得验证集的随机性小,最后取得的平均准确率更准确,而且使得数据形成重用,弥补了训练数据太少带来的不足。
(3)交叉验证与超参数选择
交叉验证往往是和超参数(比如KNN中的k,就是超参数)选择配合使用,算法工程师把模型训练出来之后,进行交叉验证,如果结果不理想怎么办?
要么更换算法,要么调整超参数,调整超参数之后,重新做一轮交叉验证,直到超参数的选择满足条件。
调参的时候,切忌出现以下情况
在(1)完成之后,调整一下超参数,(2)完成之后,又调整一下超参数。
超参数的调整,应该在(1)(2)(3)(4)四个步骤完整执行完再调整,否则不同的超参数得出的模型,因为训练集和验证集不一样,准确率无法比较。
(4)超参数的网格化搜索
如果只有一个超参数,比如KNN,那么用k=1, 3, 5一个个试,每次都进行一轮交叉验证,分别比较准确率。
如果有多个超参数,则进行网格搜索。
比如有两个超参数a和b,已知a可以取2,3,5,b可以取20,40,60,a和b之间有3×3=9种不同组合,对于每一种情况,进行一次交叉验证。
(5)交叉验证和网格化搜索的API
sklearn.model_selection.GridSearchCV(estimator, param_grid=None, cv=None, scoring=None)
对估计器的指定参数值进行详尽搜索
estimator:估计器对象
param_grid:估计器参数(使用字典),如{“n_neighbors”:[1,3,5]}
cv:指定几折交叉验证
scoring:评价指标,比如准确率、精确率、召回率、F1分数等,如果未指定,则使用准确率
调用方法
方法:
fit(x_train, y_train):输入训练数据
score(x, y):给定数据在最佳模型对应的分数
结果分析:
best_score_:在交叉验证中的最好结果
best_estimator_:最好的参数模型
best_params_:最佳的超参数组合
以前面鸢尾花数据作为例子
# -*- coding:utf-8 -*-
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, GridSearchCV
# 导入数据
iris = load_iris()
# 划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(iris["data"], iris["target"], test_size=0.25)
# 标准化
std = StandardScaler()
x_train = std.fit_transform(x_train)
x_test = std.transform(x_test)
# 实例化KNN工具,n_neighbors使用默认值还是另外指定,不影响后面的调参
knn = KNeighborsClassifier()
# 指定超参数的范围
para = {"n_neighbors": [1, 3, 5, 7]}
# 初始化GridSearchCV对象,指定二折交叉验证
gc = GridSearchCV(knn, param_grid=para, cv=2)
# 进行交叉验证
gc.fit(x_train, y_train)
# 返回最好的模型,其实就是最好的超参数对应的模型
print("最好的模型", gc.best_estimator_)
# 交叉验证中最好的结果,其实就是最适合的超参数在验证集上的平均得分
print("最好的得分", gc.best_score_)
# 使用最好的模型,对给定数据计算得分
score = gc.score(x_test, y_test)
print("给定数据在最好模型上的得分", score)
# 验证gc.score(x_test, y_test)是否为最适合模型的结果
knn = gc.best_estimator_
knn.fit(x_train, y_train)
accuracy = knn.score(x_test, y_test)
print(accuracy)
# 这里我就不输出了 自己测试一下就行
从上面的程序可以看到score(x, y)为给定数据在最佳模型对应的分数