BNN系列-Dropout as a Bayesian Approximation

本篇是对牛津大神YARIN GAL2016年论文 Dropout as a Bayesian Approximation(截止目前引用量高达2332)的阅读笔记，更具体的细节大家可以参考YARIN GAL大神的博士论文！

预备知识：

变分推断(Variational inference)

参考：博客1 博客2
变分推断:需要的分布P不容易表达/直接求解时,寻找容易表达和求解的分布Q去近似P；另外要了解在最小化KL(P||Q)时等价于最小化evidence lower bound(ELBO)（证明见上面两个博客，P(X)是定值，最小化第二项，就相当于最大化第一项ELBO）

正文

BNN把权重和偏置(后面就说权重了)从确定的值变成分布distributions(这很贝叶斯)即$\omega$~$\mathrm{p}(\omega |\mathrm{X},\mathrm{Y})$,根据贝叶斯公式可以得到$\mathrm{p}(\omega |\mathrm{X},\mathrm{Y})=\frac{\mathrm{p}(Y|\omega ,X)\mathrm{p}(\omega )}{\mathrm{p}(Y|X)}$，但是这个很难/无法计算，因此用变分推断(Variational inference)的方法：
即$q_{\theta }(\omega )$来近似$\mathrm{p}(\omega |\mathrm{X},\mathrm{Y})$那么就变成优化变分参数$\theta$（这里面的$\theta$是某一个分布的参数，后面就会知道这个参数实际就是权重 $\omega$），那么我们就需要最小化$q_{\theta }(\omega )$和$\mathrm{p}(\omega |\mathrm{X},\mathrm{Y})$之间的KL散度(优化变量为 $\theta$)：
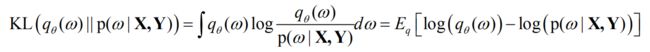根据预备知识，我们知道等价于优化$\mathrm{P}(\mathrm{X}|\mathrm{Y})$的log似然的evidence lower bound(ELBO):

使得ELBO最大化的那个$\theta$是使得$q_{\theta }(\omega )$能够最好的近似后然概率$\mathrm{p}(\omega |\mathrm{X},\mathrm{Y})$，由于该积分对于几乎所有$q_{\theta }(\omega )$都是难解的，因此我们将通过Monte Carlo方法来近似该积分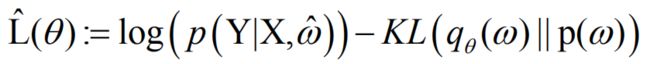
其中 $\hat{\omega }$从$q_{\theta }(\omega )$分布中采样
解读：其实这个公式很好理解，一方面要使得模型预测出Y的似然概率最大，另一方面近似的$q_{\theta }(\omega )$尽可能的接近原来的先验概率分布(一般取$N(0,I)$)。

优化的过程就可以变成：
repeatedly do:
a): sample $\hat{\omega }$~$q_{\theta }(\omega )$
b): Do one step of maximizationw.r.t. $\theta$:

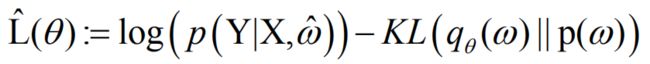
而这时的关键就是我们取什么样的$q_{\theta }(\omega )$
我们可以取

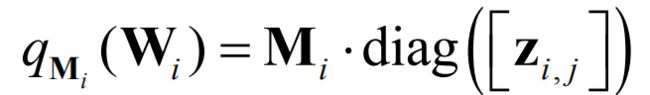
其中

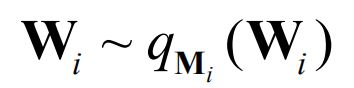
解释一下这个公式：从Bernoulli采样对角元素z等于0，即将M的列随机设置为零，这与将网络的神经单元单位随机设置为零相同。更进一步就理解：这里面变分参数就是M,而M就是没有drop out那个Standard的NN(Wi是drop out采样后的权重，相当于另一个NN了)
而采取Bernoulli分布可以使得计算变得简单，另外很好的和现有的技术drop out关联起来了，这是对drop out以贝叶斯近似(Bayesian Approximation)的角度加以诠释。
们现在有了$q_{\theta }(\omega )$具体形式，那么我们可以来继续优化$\hat{L}(\theta )$了：

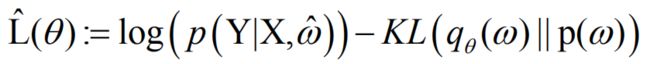
那么第一项很明显就是如果把$P(Y|X,\omega )$看成高斯分布的话(把方差看成global的常数就是传统的MSE，若是data-dependent参数的话就引入了data uncertainty这里暂不考虑)就是在优化MSE，如果看成拉普拉斯分布的话就是在优化MAE。
第二项在基于上面给出的$q_{\theta }(\omega )$的分布的情况下是在对权重做L2正则(具体推导较长，但其实不难，就用到了Gaussian processes,variational inference，具体可见YARIN GAL大神的博士论文以及他的ICML2016的论文Dropout as a Bayesian Approximation）

那么就可以理解为训练的过程中drop out+权重L2正则(weight decay)就是在用学习$q_{\theta }(\omega )$逼近后验概率。推断的时候用dropout相当于对于学习到的$q_{\theta }(\omega )$进行MC采样，便很容易近似得到预测Y的分布，便可以对model uncertainty进行量化。具体如何量化可以参见下一篇文章

其他参考：
1.贝叶斯深度学习（bayesian deep learning)
2.Medium 博客 Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning