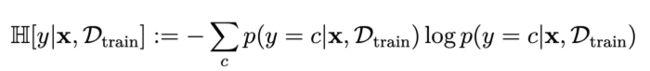测量模型不确定性的两种简单方法
在本文中,我们将介绍两种方法,它们允许你获得模型的不确定性:蒙特卡罗Dropout法(MC Dropout)和深度集成法。
它们适用于各种各样的任务,但在本文中,我们将展示一个图像分类的示例。它们都相对容易理解和实现,都可以很容易地应用于任何现有的卷积神经网络架构(例如ResNet、VGG、RegNet等)。
为了帮助你快速轻松地应用这些技术,我将提供用PyTorch编写的这些技术的补充代码。
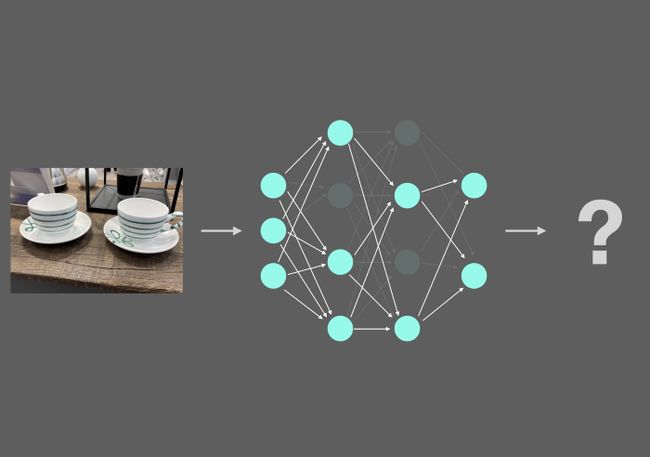
给出两个杯子的图像,你的预测模型有多确定?
在我们开始之前,让我们回顾一下测量模型不确定性意味着什么,以及它如何对你的机器学习项目有用。
什么是模型不确定性?
就像人类一样,机器学习模型可以对其预测显示一定程度的信心。一般来说,在讨论模型不确定性时,需要区分了认知不确定性和任意不确定性。
认知不确定性是在模型参数中表示的不确定性。这种类型的不确定性可以通过额外的训练数据来减少,因此具有“可减少的不确定性”的替代名称。
任意不确定性捕获环境固有的噪声,即观测。与认知不确定性相比,这种类型的不确定性不能用更多的数据来减少,而是用更精确的传感器输出来减少。
第三种类型称为预测不确定性,即模型输出中传递的不确定性。预测不确定性可以结合认知不确定性和任意不确定性。
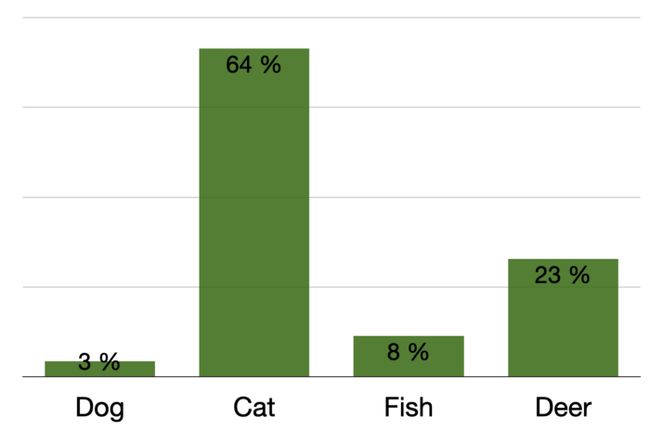
分类器的softmax输出示例:
如果你自己已经训练过简单的神经网络,那么最直观的想法就是模型的softmax输出,即你经常看到的作为模型预测结果显示的百分比值。
但是,使用softmax输出作为模型不确定性的度量可能会产生误导,并且不是很有用。这是因为softmax函数所做的只是计算模型不同激活值之间的某种“关系”。
因此,你的模型可以在其输出层的所有神经元中具有较低的激活值,并且仍然达到较高的softmax值。这不是我们的目标。但值得庆幸的是,有多种更有效的技术来估计模型的不确定性,如蒙特卡罗Dropout和深度集成。
为什么模型不确定性有用?
有两个主要方面使评估模型的不确定性变得有用:
首先是透明度。假设你正在构建一个应用于医学图像分析的机器学习模型。因此,使用你的工具的医生在很大程度上依赖于其做出正确诊断的能力。
如果你的模型现在做出了一个预测,它实际上是高度不确定的,但确实将此信息传达给了医生,那么对患者治疗的后果可能是致命的。因此,对模型的不确定性进行估计可以在很大程度上帮助医生判断模型的预测。
第二是显示出改进的空间。没有一种机器学习模型是完美的。因此,了解模型的不确定性和弱点实际上可以告诉你需要对模型进行哪些改进。
实际上,有一门完整的学科专门研究这门学科,叫做主动学习。假设你已经用1000张图片和10个类训练了你的ConvNet。但你仍然有9000多张尚未标记的图像。如果你现在使用经过训练的模型来预测哪些图像是最不确定的,则标记这些图像并重新训练模型。结果表明,与这些图像的随机抽样相比,这种不确定性抽样对模型改进更有效。
好了,让我们来讨论这两种技术。
技巧1:蒙特卡罗Dropout
Monte Carlo Dropout,简称MC Dropout,是一种在模型中使用Dropout层来创建模型输出变化的技术。
应用于神经网络的Dropout可视化。
Dropout层通常在训练期间用作正则化技术。在向前通过网络的过程中,某些神经元以一定的概率随机为0。这表明,该模型具有更强的抗过拟合能力。
通常,为了不干扰新图像的前向传递,在训练后禁用这些Dropout层。所以,要使用这种技术,请确保在你的模型中至少实现一个Dropout层。这可能看起来像这样。
import torch
import torch.nn as nn
import torch.nn.functional as F
class Model(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
# 定义 0.25 dropout概率
self.dropout = nn.Dropout(0.25)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = torch.flatten(x, 1)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
# Dropout
x = self.dropout(x)
x = self.fc3(x)
return x
model = Model()但是对于MC Dropout,Dropout层仍然被激活,这意味着神经元仍然可以随机为0。这导致模型的softmax结果发生变化。要在推理或测试期间使用Dropout,请使用以下代码:
for module in model.modules():
if module.__class__.__name__.startswith('Dropout'):
module.train()现在Dropout仍然可用,因为我们已经把所有Dropout层进入训练模式!
假设我们现在想在一张图像上获得模型的不确定性。为此,我们不仅要对图像进行一次预测,还要进行多次预测,并分析由多个前向传播生成的不同输出。我建议让模型在一张图像上预测3到5次。在本文末尾,我将介绍如何组合3或5个输出。
技巧2:深层集成
第二种估计模型不确定性的技术利用了创建模型集合的优势。与其使用一个模型并预测5次,不如使用同一类型的多个模型,随机初始化它们的权重,并根据相同的数据对它们进行训练。
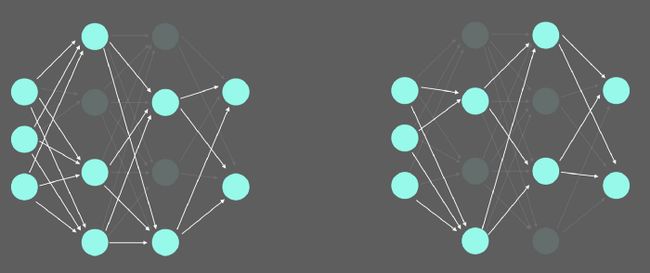
多个神经网络集成的可视化:
这也将在模型参数中创建变化。如果模型经过稳健训练,并且对图像有把握,它将为每个前向传播输出类似的值。
要初始化模型,最好将其保存为模型列表:
# 我们的集成中要有多少个模型
n_ensemble = 5
# 初始化集合
ensemble = [Model() for e_model in range(n_ensemble)]初始化后,所有模型都将在相同的训练数据上进行训练。就像MC Dropout者一样,3或5个模型是一个不错的选择。
为了获得给定图像上模型的不确定性,将其传递到集合中的每个模型中,并将其预测组合起来进行分析。
组合来自多个前向传播的模型输出
假设我们为MC Dropout定义了5次前向传播过程,集成模型包含5个模型。
现在,我们预计这些输出之间会出现一些变化,从而显示出模型的不确定性。
为了得到不确定性的最终值,必须首先对这些输出进行叠加。这段代码是一个例子,说明了如何实现MCDropout:
import numpy as np
fwd_passes = 5
predictions = []
for fwd_pass in range(fwd_passes):
output = model(image)
np_output = output.detach().cpu().numpy()
if fwd_pass == 0:
predictions = np_output
else:
predictions = np.vstack((predictions, np_output))首先,我们定义要执行的前向传播及保存所有预测的空列表。然后我们前向传播5次。第一个输出用作结果numpy数组的初始化,所有其他输出都堆叠在顶部。
这是具有相同基本原则的深层集成代码:
import numpy as np
predictions = []
for i_model, model in enumerate(ensemble):
output = model(image)
np_output = output.detach().cpu().numpy()
if i_model == 0:
predictions = np_output
else:
predictions = np.vstack((predictions, np_output))现在我们已经组合了所有输出,让我们看看如何从这些输出计算模型的不确定性。
获取模型不确定性
为了简单起见,我们将使用预测熵来估计给定图像上模型的不确定性。
预测熵的数学公式为y(标签)、x(输入图像)、Dtrain(训练数据)、c(类)、p(概率)。
一般来说,预测不确定性告诉你模型看到这张图像时有多“惊讶”。如果该值较低,则模型对其预测是确定的。如果结果为高,则模型不知道图像中的内容。
计算预测不确定度可以通过这段代码来实现,这段代码接收预测数组作为输入。
import sys
import numpy as np
def predictive_entropy(predictions):
epsilon = sys.float_info.min
predictive_entropy = -np.sum( np.mean(predictions, axis=0) * np.log(np.mean(predictions, axis=0) + epsilon),
axis=-1)
return predictive_entropy方程中的ε阻止了除0,这在数学上是没有定义的。
好吧现在,你有了一个图像的不确定性值。如前所述,值越高,模型的不确定性越大。
结尾
在本文中,你已经学会了估计模型的不确定性。这项技术也可以通过一些调整应用于目标检测,它非常强大。
参考资料:
[1] Uncertainty in Deep Learning, Yarin Gal. http://mlg.eng.cam.ac.uk/yarin/thesis/thesis.pdf
☆ END ☆
如果看到这里,说明你喜欢这篇文章,请转发、点赞。微信搜索「uncle_pn」,欢迎添加小编微信「 woshicver」,每日朋友圈更新一篇高质量博文。
↓扫描二维码添加小编↓