算法笔记(10)支持向量机SVM及Python代码实现
支持向量:在训练数据集中,只有一部分数据对于边界的确定是有帮助的,而这些数据点就是正好位于决定边界上的,这些数据被称为“支持向量”。
最大边界间隔超平面:两类样本分别分割在该超平面的两侧,两侧距离超平面最近的样本点到超平面的距离被最大化了。
SVM算法的核函数功能:将数据投射到高维空间。
SVM算法常用核函数:线性核函数 LINEAR、高斯径向基核函数 RBF、多项式核函数 POLY、神经元的非线性作用核函数 Sigmoid。
优点:SVM算法对高维数据集和低维数据集都表现不错,
缺点:数据集规模不太大,对于数据预处理和参数调节要求非常高
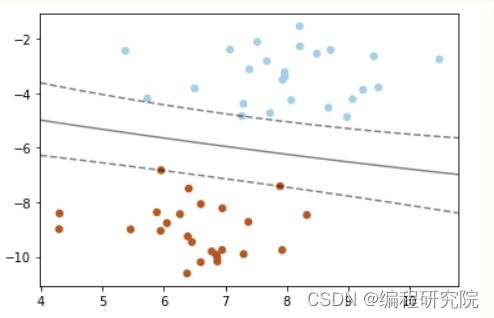
线性内核的SVM分类器
python代码实现
# 创建一个线性内核的支持向量机模型
clf = svm.SVC(kernel='linear', C=1000)
clf.fit(X, y)
# 把数据点画出来
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.Paired)
#建立图像坐标
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)
# 把分类的决定边界画出来
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=100,
linewidth=1, facecolors='none')
plt.show()输出结果展示如下:
RBF内核的SVM分类器
python代码实现
# 创建一个RBF内核的支持向量机模型
clf_rbf = svm.SVC(kernel='rbf', C=1000)
clf_rbf.fit(X, y)
# 把数据点画出来
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.Paired)
#建立图像坐标
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = clf_rbf.decision_function(xy).reshape(XX.shape)
# 把分类的决定边界画出来
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
ax.scatter(clf_rbf.support_vectors_[:, 0], clf_rbf.support_vectors_[:, 1], s=100,
linewidth=1, facecolors='none')
plt.show()输出结果展示如下:
想要完整代码的朋友,可toutiao号搜索“编程研究坊”关注后私信我,回复“算法笔记10“免费获取