机器学习-Sklearn-05（逻辑回归）

机器学习-Sklearn-05（逻辑回归与评分卡）

学习05

sklearn中的逻辑回归

1 概述

1.1 名为“回归”的分类器

在过去的四周中，我们接触了不少带“回归”二字的算法，回归树，随机森林的回归，无一例外他们都是区别于分类算法们，用来处理和预测连续型标签的算法。然而逻辑回归，是一种名为“回归”的线性分类器，其本质是由线性回归变化而来的，一种广泛使用于分类问题中的广义回归算法。

要理解逻辑回归从何而来，得要先理解线性回归。线性回归是机器学习中最简单的的回归算法，它写作一个几乎人人熟悉的方程：

θ被统称为模型的参数，其中θ0被称为截距(intercept)，θ1~θn 被称为系数(coefficient)，这个表达式，其实就和我们小学时就无比熟悉的 y = ax + b 是同样的性质。我们可以使用矩阵来表示这个方程，其中x和θ都可以被看做是一个列矩阵，则有：

线性回归的任务，就是构造一个预测函数 来映射输入的特征矩阵x和标签值y的线性关系，而构造预测函数的核心就是找出模型的参数：θ^T和θ0 ，著名的最小二乘法就是用来求解线性回归中参数的数学方法。

通过函数 ，线性回归使用输入的特征矩阵X来输出一组连续型的标签值y_pred，以完成各种预测连续型变量的任务（比如预测产品销量，预测股价等等）。那如果我们的标签是离散型变量，尤其是，如果是满足0-1分布的离散型变量，我们要怎么办呢？我们可以通过引入联系函数(link function)，将线性回归方程z变换为g(z)，并且令g(z)的值分布在(0,1)之间，且当g(z)接近0时样本的标签为类别0，当g(z)接近1时样本的标签为类别1，这样就得到了一个分类模型。而这个联系函数对于逻辑回归来说，就是Sigmoid函数：


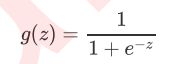
面试高危问题：Sigmoid函数的公式和性质
Sigmoid函数是一个S型的函数，当自变量z趋近正无穷时，因变量g(z)趋近于1，而当z趋近负无穷时，g(z)趋近于0，它能够将任何实数映射到(0,1)区间，使其可用于将任意值函数转换为更适合二分类的函数。

因为这个性质，Sigmoid函数也被当作是归一化的一种方法，与我们之前学过的MinMaxSclaer同理，是属于数据预处理中的“缩放”功能，可以将数据压缩到[0,1]之内。区别在于，MinMaxScaler归一化之后，是可以取到0和1的（最大值归一化后就是1，最小值归一化后就是0），但Sigmoid函数只是无限趋近于0和1。

而 就是我们逻辑回归返回的标签值。此时， 的取值都在[0,1]之间，因此y(x)和1-y(x)相加必然为1。如果我们令y(x)除以1-y(x)可以得到形似几率(odds)的 y(x)/(1 - y(x))，在此基础上取对数，可以容易就得到：

不难发现，y(x)的形似几率取对数的本质其实就是我们的线性回归z，我们实际上是在对线性回归模型的预测结果取对数几率来让其的结果无限逼近0和1。因此，其对应的模型被称为**”对数几率回归“（logistic Regression），也就是我们的逻辑回归**，这个名为“回归”却是用来做分类工作的分类器。

之前我们提到过，线性回归的核心任务是通过求解 构建 这个预测函数，并希望预测函数 能够尽量拟合数据，因此逻辑回归的核心任务也是类似的：求解 来构建一个能够尽量拟合数据的预测函数 ，并通过向预测函数中输入特征矩阵来获取相应的标签值y。

思考：y(x)代表了样本为某一类标签的概率吗？

1.2 为什么需要逻辑回归

无论机器学习领域如何折腾，逻辑回归依然是一个受工业商业热爱，使用广泛的模型，因为它有着不可替代的优点：
1、逻辑回归对线性关系的拟合效果好到丧心病狂；
2、逻辑回归计算快；
3、逻辑回归返回的分类结果不是固定的0，1，而是以小数形式呈现的类概率数字；
由此，我们已经了解了逻辑回归的本质，它是一个返回对数几率的，在线性数据上表现优异的分类器，它主要被应用在金融领域。**其数学目的是求解能够让模型对数据拟合程度最高的参数θ的值，以此构建预测函数 ，然后将特征矩阵输入预测函数来计算出逻辑回归的结果y。**注意，虽然我们熟悉的逻辑回归通常被用于处理二分类问题，但逻辑回归也可以做多分类。

1.3 sklearn中的逻辑回归

2 linear_model.LogisticRegression

2.1 二元逻辑回归的损失函数

2.1.1 损失函数的概念与解惑

在学习决策树和随机森林时，我们曾经提到过两种模型表现：在训练集上的表现，和在测试集上的表现。我们建模，是追求模型在测试集上的表现最优，因此模型的评估指标往往是用来衡量模型在测试集上的表现的。然而，逻辑回归有着基于训练数据求解参数 的需求，并且希望训练出来的模型能够尽可能地拟合训练数据，即模型在训练集上的预测准确率越靠近100%越好。

因此，我们使用**”损失函数“**这个评估指标，**来衡量参数为θ的模型拟合训练集时产生的信息损失的大小，并以此衡量参数θ的优劣。**如果用一组参数建模后，模型在训练集上表现良好，那我们就说模型拟合过程中的损失很小，损失函数的值很小，这一组参数就优秀；相反，如果模型在训练集上表现糟糕，损失函数就会很大，模型就训练不足，效果较差，这一组参数也就比较差。即是说，我们在求解参数 时，追求损失函数最小，让模型在训练数据上的拟合效果最优，即预测准确率尽量靠近100%。

关键概念：损失函数

衡量参数 的优劣的评估指标，用来求解最优参数的工具
损失函数小，模型在训练集上表现优异，拟合充分，参数优秀
损失函数大，模型在训练集上表现差劲，拟合不足，参数糟糕
我们追求，能够让损失函数最小化的参数组合

注意：没有”求解参数“需求的模型（即不需要求解θ的模型）没有损失函数，比如KNN，决策树。

逻辑回归的损失函数是由极大似然估计推导出来的，具体结果可以写作：

逻辑回归的损失函数是由极大似然估计推导出来的，具体结果可以写作：


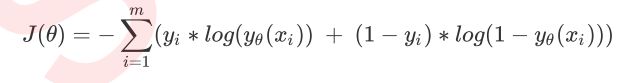
由于我们追求损失函数的最小值，让模型在训练集上表现最优，可能会引发另一个问题：**如果模型在训练集上表示优秀，却在测试集上表现糟糕，模型就会过拟合。**虽然逻辑回归和线性回归是天生欠拟合的模型，但我们还是需要控制过拟合的技术来帮助我们调整模型，对逻辑回归中过拟合的控制，通过正则化来实现。

2.2 重要参数penalty & C

2.2.1 正则化

正则化是用来防止模型过拟合的过程，常用的有L1正则化和L2正则化两种选项，分别通过在损失函数后加上参数向量 的L1范式和L2范式的倍数来实现。这个增加的范式，被称为“正则项”，也被称为"惩罚项"。损失函数改变，基于损失函数的最优化来求解的参数取值必然改变，我们以此来调节模型拟合的程度。其中L1范式表现为参数向量中的每个参数的绝对值之和，L2范数表现为参数向量中的每个参数的平方和的开方值。

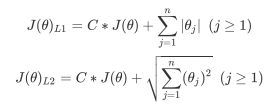
其中 是我们之前提过的损失函数，C是用来控制正则化程度的超参数，n是方程中特征的总数，也是方程中参数的总数，j代表每个参数。在这里，j要大于等于1，是因为我们的参数向量 中，第一个参数是 ，是我们的截距，它通常是不参与正则化的。
在许多书籍和博客中，大家可能也会见到如下的写法：

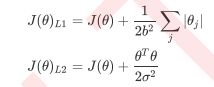
其实和上面我们展示的式子的本质是一模一样的。不过在大多数教材和博客中，常数项是乘以正则项，通过调控正则项来调节对模型的惩罚。而sklearn当中，常数项C是在损失函数的前面，通过调控损失函数本身的大小，来调节对模型的惩罚。

L1正则化和L2正则化虽然都可以控制过拟合，但它们的效果并不相同。当正则化强度逐渐增大（即C逐渐变小），参数 的取值会逐渐变小，但L1正则化会将参数压缩为0，L2正则化只会让参数尽量小，不会取到0。

在L1正则化在逐渐加强的过程中，携带信息量小的、对模型贡献不大的特征的参数，会比携带大量信息的、对模型有巨大贡献的特征的参数更快地变成0，所以L1正则化本质是一个特征选择的过程，掌管了参数的“稀疏性”。L1正则化越强，参数向量中就越多的参数为0，参数就越稀疏，选出来的特征就越少，以此来防止过拟合。因此，如果特征量很大，数据维度很高，我们会倾向于使用L1正则化。由于L1正则化的这个性质，逻辑回归的特征选择可以由Embedded嵌入法来完成。

相对的，L2正则化在加强的过程中，会尽量让每个特征对模型都有一些小的贡献，但携带信息少，对模型贡献不大的特征的参数会非常接近于0。通常来说，如果我们的主要目的只是为了防止过拟合，选择L2正则化就足够了。但是如果选择L2正则化后还是过拟合，模型在未知数据集上的效果表现很差，就可以考虑L1正则化。

而两种正则化下C的取值，都可以通过学习曲线来进行调整。

建立两个逻辑回归，L1正则化和L2正则化的差别就一目了然了：
#L1正则化和L2正则化的差别
#导入类
from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer #乳腺癌数据集
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

data = load_breast_cancer()
data.data #特征矩阵

data.target #标签矩阵

X = data.data
y = data.target
data.data.shape

lrl1 = LR(penalty=“l1”,solver=“liblinear”,C=0.5,max_iter=1000)
lrl2 = LR(penalty=“l2”,solver=“liblinear”,C=0.5,max_iter=1000)

#逻辑回归的重要属性coef_，查看每个特征所对应的参数
lrl1 = lrl1.fit(X,y)
lrl1.coef_ #虽然有30个特征，但有很多特征都是0

lrl1.coef_ != 0

(lrl1.coef_ != 0).sum(axis=1)

lrl2 = lrl2.fit(X,y)
lrl2.coef_ #有30个特征，但有没有特征为0

lrl2.coef_ != 0

(lrl2.coef_ != 0).sum(axis=1)

#绘制C超参数学习曲线
l1 = []
l2 = []
l1test = []
l2test = []

Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)

for i in np.linspace(0.05,2,19):

lrl1 = LR(penalty="l1",solver="liblinear",C=i,max_iter=1000)
lrl2 = LR(penalty="l2",solver="liblinear",C=i,max_iter=1000)

lrl1 = lrl1.fit(Xtrain,Ytrain)
l1.append(accuracy_score(lrl1.predict(Xtrain),Ytrain))
l1test.append(accuracy_score(lrl1.predict(Xtest),Ytest))

lrl2 = lrl2.fit(Xtrain,Ytrain)
l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain))
l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest))

graph = [l1,l2,l1test,l2test]
color = [“green”,“black”,“lightgreen”,“gray”]
label = [“L1”,“L2”,“L1test”,“L2test”]

plt.figure(figsize=(6,6))
for i in range(len(graph)):
plt.plot(np.linspace(0.05,2,19),graph[i],color[i],label=label[i])
plt.legend(loc=4) #图例的位置在哪里?4表示，右下角
plt.show()

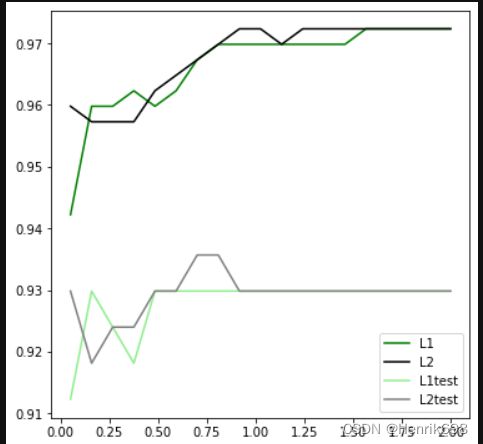
可见，至少在我们的乳腺癌数据集下，两种正则化的结果区别不大。但随着C的逐渐变大，正则化的强度越来越小，模型在训练集和测试集上的表现都呈上升趋势，直到C=0.8左右，训练集上的表现依然在走高，但模型在未知数据集上的表现开始下跌，这时候就是出现了过拟合。我们可以认为，C设定为0.8会比较好。在实际使用时，基本就默认使用l2正则化，如果感觉到模型的效果不好，那就换L1试试看。

2.2.2 逻辑回归中的特征工程

当特征的数量很多的时候，我们出于业务考虑，也出于计算量的考虑，希望对逻辑回归进行特征选择来降维。比如，在判断一个人是否会患乳腺癌的时候，医生如果看5~8个指标来确诊，会比需要看30个指标来确诊容易得多。

业务选择
说到降维和特征选择，首先要想到的是利用自己的业务能力进行选择，肉眼可见明显和标签有关的特征就是需要留下的。当然，如果我们并不了解业务，或者有成千上万的特征，那我们也可以使用算法来帮助我们。或者，可以让算法先帮助我们筛选过一遍特征，然后在少量的特征中，我们再根据业务常识来选择更少量的特征。

PCA和SVD一般不用
说到降维，我们首先想到的是之前提过的高效降维算法，PCA和SVD，遗憾的是，这两种方法大多数时候不适用于逻辑回归。逻辑回归是由线性回归演变而来，线性回归的一个核心目的是通过求解参数来探究特征X与标签y之间的关系，而逻辑回归也传承了这个性质，我们常常希望通过逻辑回归的结果，来判断什么样的特征与分类结果相关，因此我们希望保留特征的原貌。PCA和SVD的降维结果是不可解释的，因此一旦降维后，我们就无法解释特征和标签之间的关系了。当然，在不需要探究特征与标签之间关系的线性数据上，降维算法PCA和SVD也是可以使用的。

统计方法可以使用，但不是非常必要
既然降维算法不能使用，我们要用的就是特征选择方法。逻辑回归对数据的要求低于线性回归，由于我们不是使用最小二乘法来求解，所以逻辑回归对数据的总体分布和方差没有要求，也不需要排除特征之间的共线性，但如果我们确实希望使用一些统计方法，比如方差，卡方，互信息等方法来做特征选择，也并没有问题。过滤法中所有的方法，都可以用在逻辑回归上。

在一些博客中有这样的观点：多重共线性会影响线性模型的效果。对于线性回归来说，多重共线性会影响比较大，所以我们需要使用方差过滤和方差膨胀因子VIF(variance inflation factor)来消除共线性。但是对于逻辑回归，其实不是非常必要，甚至有时候，我们还需要多一些相互关联的特征来增强模型的表现。当然，如果我们无法通过其他方式提升模型表现，并且你感觉到模型中的共线性影响了模型效果，那懂得统计学的你可以试试看用VIF消除共线性的方法，遗憾的是现在sklearn中并没有提供VIF的功能。

高效的嵌入法embedded
但是更有效的方法，毫无疑问会是我们的embedded嵌入法。我们已经说明了，由于L1正则化会使得部分特征对应的参数为0，因此L1正则化可以用来做特征选择，结合嵌入法的模块SelectFromModel，我们可以很容易就筛选出让模型十分高效的特征。注意，此时我们的目的是，尽量保留原数据上的信息，让模型在降维后的数据上的拟合效果保持优秀，因此我们不考虑训练集测试集的问题，把所有的数据都放入模型进行降维。

#高效的嵌入法embedded
#导库
from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectFromModel

data = load_breast_cancer()#乳腺癌数据的实例化
data.data.shape

LR_ = LR(solver=“liblinear”,C=0.8,random_state=420)
cross_val_score(LR_,data.data,data.target,cv=10).mean()

#对数据进行降维
X_embedded = SelectFromModel(LR_,norm_order=1).fit_transform(data.data,data.target)
X_embedded.shape

X_embedded.shape

data.target.shape

cross_val_score(LR_,X_embedded,data.target,cv=10).mean()

看看结果，特征数量被减小到个位数，并且模型的效果却没有下降太多，如果我们要求不高，在这里其实就可以停下了。但是，能否让模型的拟合效果更好呢？在这里，我们有两种调整方式：

1）调节SelectFromModel这个类中的参数threshold，这是嵌入法的阈值，表示删除所有参数的绝对值低于这个阈值的特征。现在threshold默认为None，所以SelectFromModel只根据L1正则化的结果来选择了特征，即选择了所有L1正则化后参数不为0的特征。我们此时，只要调整threshold的值（画出threshold的学习曲线），就可以观察不同的threshold下模型的效果如何变化。一旦调整threshold，就不是在使用L1正则化选择特征，而是使用模型的属性.coef_中生成的各个特征的系数来选择。coef_虽然返回的是特征的系数，但是系数的大小和决策树中的feature_ importances_以及降维算法中的可解释性方差explained_vairance_概念相似，其实都是衡量特征的重要程度和贡献度的，因此SelectFromModel中的参数threshold可以设置为coef_的阈值，即可以剔除系数小于threshold中输入的数字的所有特征。

#查看所有系数
LR_.fit(data.data,data.target).coef_

#取绝对值和最大值
abs(LR_.fit(data.data,data.target).coef_).max()

#学习曲线
fullx = []
fsx = []
threshold = np.linspace(0,abs((LR_.fit(data.data,data.target).coef_)).max(),20)
k=0
for i in threshold:

X_embedded = SelectFromModel(LR_,threshold=i).fit_transform(data.data,data.target)
fullx.append(cross_val_score(LR_,data.data,data.target,cv=5).mean())
fsx.append(cross_val_score(LR_,X_embedded,data.target,cv=5).mean())
print((threshold[k],X_embedded.shape[1]))
k+=1

plt.figure(figsize=(20,5))
plt.plot(threshold,fullx,label=“full”)
plt.plot(threshold,fsx,label=“feature selection”)
plt.xticks(threshold)
plt.legend()
plt.show()


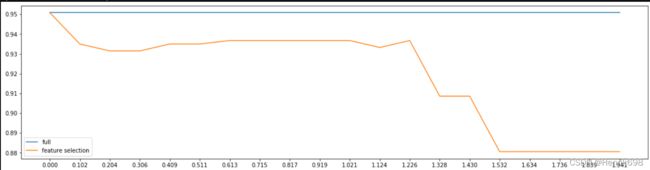
然而，这种方法其实是比较无效的，大家可以用学习曲线来跑一跑：当threshold越来越大，被删除的特征越来越多，模型的效果也越来越差，模型效果最好的情况下需要保证有17个以上的特征。实际上我画了细化的学习曲线，如果要保证模型的效果比降维前更好，我们需要保留25个特征，这对于现实情况来说，是一种无效的降维：需要30个指标来判断病情，和需要25个指标来判断病情，对医生来说区别不大。

2）第二种调整方法，是调逻辑回归的类LR_，通过画C的学习曲线来实现：
#第二种调整方法，通过画C的学习曲线来实现。
fullx = []
fsx = []
C=np.arange(0.01,10.01,0.5)
C

for i in C:

LR_ = LR(solver="liblinear",C=i,random_state=420)

fullx.append(cross_val_score(LR_,data.data,data.target,cv=10).mean())

X_embedded = SelectFromModel(LR_,norm_order=1).fit_transform(data.data,data.target)
fsx.append(cross_val_score(LR_,X_embedded,data.target,cv=10).mean())

print(max(fsx),C[fsx.index(max(fsx))])
plt.figure(figsize=(20,5))
plt.plot(C,fullx,label=“full”)
plt.plot(C,fsx,label=“feature selection”)
plt.xticks©
plt.legend()
plt.show()


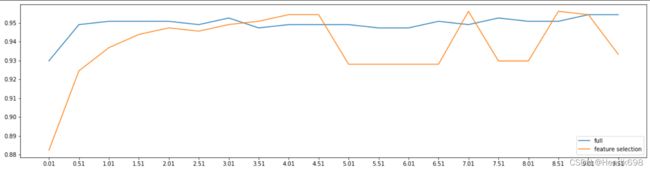
继续细化学习曲线：
#继续细化学习曲线：
fullx = []
fsx = []
C=np.arange(6.05,7.05,0.005)
for i in C:

LR_ = LR(solver="liblinear",C=i,random_state=420)

fullx.append(cross_val_score(LR_,data.data,data.target,cv=10).mean())

X_embedded = SelectFromModel(LR_,norm_order=1).fit_transform(data.data,data.target)
fsx.append(cross_val_score(LR_,X_embedded,data.target,cv=10).mean())

print(max(fsx),C[fsx.index(max(fsx))])
plt.figure(figsize=(20,5))
plt.plot(C,fullx,label=“full”)
plt.plot(C,fsx,label=“feature selection”)
plt.xticks©
plt.legend()
plt.show()


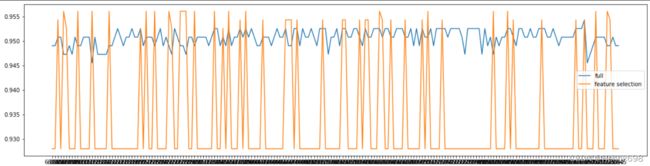
#验证模型效果：降维之前
LR_ = LR(solver=“liblinear”,C=6.069999999999999,random_state=420)
cross_val_score(LR_,data.data,data.target,cv=10).mean()

#验证模型效果：降维之后
LR_ = LR(solver=“liblinear”,C=6.069999999999999,random_state=420)
X_embedded = SelectFromModel(LR_,norm_order=1).fit_transform(data.data,data.target)
cross_val_score(LR_,X_embedded,data.target,cv=10).mean()

X_embedded.shape

这样我们就实现了在特征选择的前提下，保持模型拟合的高效，现在，如果有一位医生可以来为我们指点迷津，看看剩下的这些特征中，有哪些是对针对病情来说特别重要的，也许我们还可以继续降维。当然，除了嵌入法，系数累加法或者包装法也是可以使用的。

比较麻烦的系数累加法
系数累加法的原理非常简单。在PCA中，我们通过绘制累积可解释方差贡献率曲线来选择超参数，在逻辑回归中我们可以使用系数coef_来这样做，并且我们选择特征个数的逻辑也是类似的：找出曲线由锐利变平滑的转折点，转折点之前被累加的特征都是我们需要的，转折点之后的我们都不需要。不过这种方法相对比较麻烦，因为我们要先对特征系数进行从大到小的排序，还要确保我们知道排序后的每个系数对应的原始特征的位置，才能够正确找出那些重要的特征。如果要使用这样的方法，不如直接使用嵌入法来得方便。

简单快速的包装法
相对的，包装法可以直接设定我们需要的特征个数，逻辑回归在现实中运用时，可能会有”需要5~8个变量”这种需求，包装法此时就非常方便了。不过逻辑回归的包装法的使用和其他算法一样，并不具有特别之处，因此在这里就不在赘述，具体大家可以参考03期：数据预处理和特征工程中的代码。

2.3 梯度下降：重要参数max_iter

逻辑回归的数学目的是求解能够让模型最优化，拟合程度最好的参数 的值，即求解能够让损失函数 最小化的值。对于二元逻辑回归来说，有多种方法可以用来求解参数 ，最常见的有梯度下降法(Gradient Descent)，坐标下降法(Coordinate Descent)，牛顿法(Newton-Raphson method)等，其中又以梯度下降法最为著名。每种方法都涉及复杂的数学原理，但这些计算在执行的任务其实是类似的。

2.3.1 梯度下降求解逻辑回归

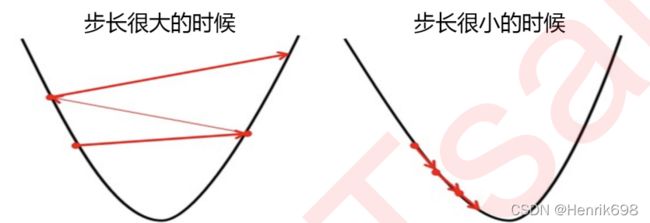
我们以最著名也最常用的梯度下降法为例，来看看逻辑回归的参数求解过程究竟实在做什么。现在有一个带两个特征并且没有截距的逻辑回归 ，两个特征所对应的参数分别为 。下面这个华丽的平面就是我们的损失函数 在以 ， 和 为坐标轴的三维立体坐标系上的图像。现在，我们寻求的是损失函数的最小值，也就是图像的最低点。

那我们怎么做呢？我在这个图像上随机放一个小球，当我松手，这个小球就会顺着这个华丽的平面滚落，直到滚到深蓝色的区域——损失函数的最低点。为了严格监控这个小球的行为，我让小球每次滚动的距离有限，不让他一次性滚到最低点，并且最多只允许它滚动100步，还要记下它每次滚动的方向，直到它滚到图像上的最低点。

可以看见，小球从高处滑落，在深蓝色的区域中来回震荡，最终停留在了图像凹陷处的某个点上。非常明显，我们可以观察到几个现象：

首先，小球并不是一开始就直向着最低点去的，它先一口气冲到了蓝色区域边缘，后来又折回来，我们已经规定了小球是多次滚动，所以可见，小球每次滚动的方向都是不同的。

另外，小球在进入深蓝色区域后，并没有直接找到某个点，而是在深蓝色区域中来回震荡了数次才停下。这有两种可能：1) 小球已经滚到了图像的最低点，所以停下了，2) 由于我设定的步数限制，小球还没有找到最低点，但也只好在100步的时候停下了。也就是说，小球不一定滚到了图像的最低处。

但无论如何，小球停下的就是我们在现有状况下可以获得的唯一点了。如果我们够幸运，这个点就是图像的最低点，那我们只要找到这个点的对应坐标(
)，就可以获取能够让损失函数最小的参数取值
了。如此，梯度下降的过程就已经完成。

在这个过程中，小球其实就是一组组的坐标点（θ1, θ2, J）；小球每次滚动的方向就是那一个坐标点的梯度向量的方向，因为每滚动一步，小球所在的位置都发生变化，坐标点和坐标点对应的梯度向量都发生了变化，所以每次滚动的方向也都不一样；人为设置的100次滚动限制，就是sklearn中逻辑回归的参数max_iter，代表着能走的最大步数，即最大迭代次数。

所以梯度下降，其实就是在众多[θ1, θ2]可能的值中遍历，一次次求解坐标点的梯度向量，不断让损失函数的取值 J 逐渐逼近最小值，再返回这个最小值对应的参数取值
的过程。

2.3.2 梯度下降的概念与解惑

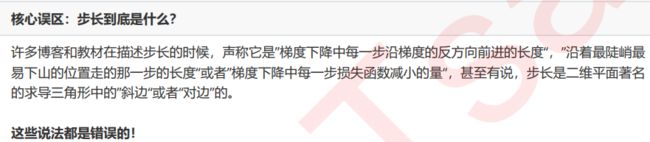
核心误区：到底在哪个函数上，求什么的偏导数？

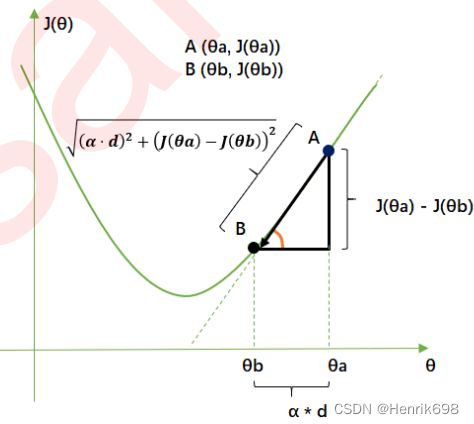
那梯度有什么含义呢？梯度是一个向量，因此它有大小也有方向。它的大小，就是偏导数组成的向量的大小，又叫做向量的模，记作 。它的方向，几何上来说，就是损失函数J(θ)的值增加最快的方向，就是小球每次滚动的方向的反方向。只要沿着梯度向量的反方向移动坐标，损失函数J(θ)的取值就会减少得最快，也就最容易找到损失函数的最小值。

在逻辑回归中，我们的损失函数如下所示：

我们对这个函数上的自变量θ求偏导，就可以得到梯度向量在第 j 组θ的坐标点上的表示形式：

2.3.3 步长的概念与解惑

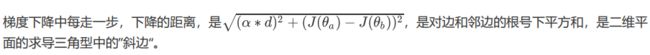
所以，步长不是任何物理距离，它甚至不是梯度下降过程中任何距离的直接变化，它是梯度向量的大小 d上的一个比例，影响着参数向量θ每次迭代后改变的部分。



来看看乳腺癌数据集下，max_iter的学习曲线：
#控制步长max_iter
#导入类
from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer #乳腺癌数据集
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

data = load_breast_cancer()
data.data #特征矩阵

X = data.data
y = data.target
data.data.shape

l2 = []
l2test = []
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)

for i in np.arange(1,201,10):

lrl2 = LR(penalty="l2",solver="liblinear",C=0.8,max_iter=i)
lrl2 = lrl2.fit(Xtrain,Ytrain)
l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain))
l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest))

graph = [l2,l2test]
color = [“black”,“gray”]
label = [“L2”,“L2test”]

plt.figure(figsize=(20,5))

for i in range(len(graph)):

plt.plot(np.arange(1,201,10),graph[i],color[i],label=label[i])

plt.legend(loc=4)
plt.xticks(np.arange(1,201,10))
plt.show()

#我们可以使用属性.n_iter_来调用本次求解中真正实现的迭代次数
lr = LR(penalty=“l2”,solver=“liblinear”,C=0.8,max_iter=300).fit(Xtrain,Ytrain)
lr.n_iter_

#我们可以使用属性.n_iter_来调用本次求解中真正实现的迭代次数
#如果max_iter为10时：
lr = LR(penalty=“l2”,solver=“liblinear”,C=0.8,max_iter=10).fit(Xtrain,Ytrain)
lr.n_iter_

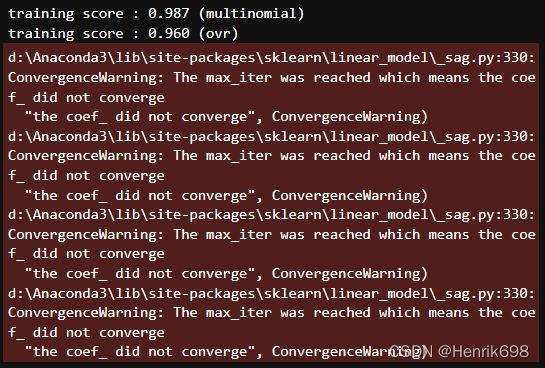
当max_iter中限制的步数已经走完了，逻辑回归却还没有找到损失函数的最小值，参数 的值还没有被收敛，sklearn就会弹出这样的红色警告：
当参数solver=“liblinear”：

当参数solver=“sag”：

虽然写法看起来略有不同，但其实都是一个含义，这是在提醒我们：参数没有收敛，请增大max_iter中输入的数字。但我们不一定要听sklearn的。max_iter很大，意味着步长小，模型运行得会更加缓慢。虽然我们在梯度下降中追求的是损失函数的最小值，但这也可能意味着我们的模型会过拟合（在训练集上表现得太好，在测试集上却不一定），因此，如果在max_iter报红条的情况下，模型的训练和预测效果都已经不错了，那我们就不需要再增大max_iter中的数目了，毕竟一切都以模型的预测效果为基准——只要最终的预测效果好，运行又快，那就一切都好，无所谓是否报红色警告了。

2.4 二元回归与多元回归：重要参数solver & multi_class

之前我们对逻辑回归的讨论，都是针对二分类的逻辑回归展开，其实sklearn提供了多种可以使用逻辑回归处理多分类问题的选项。比如说，我们可以把某种分类类型都看作1，其余的分类类型都为0值，和”数据预处理“中的二值化的思维类似，这种方法被称为"一对多"(One-vs-rest)，简称OvR，在sklearn中表示为“ovr"。又或者，我们可以把好几个分类类型划为1，剩下的几个分类类型划为0值，这是一种”多对多“(Many-vs-Many)的方法，简称MvM，在sklearn中表示为"Multinominal"。每种方式都配合L1或L2正则项来使用。

在sklearn中，我们使用参数multi_class来告诉模型，我们的预测标签是什么样的类型。

multi_class
输入"ovr", “multinomial”, “auto"来告知模型，我们要处理的分类问题的类型。默认是"ovr”。
‘ovr’:表示分类问题是二分类，或让模型使用"一对多"的形式来处理多分类问题。
‘multinomial’：表示处理多分类问题，这种输入在参数solver是’liblinear’时不可用。
“auto”：表示会根据数据的分类情况和其他参数来确定模型要处理的分类问题的类型。比如说，如果数据是二分类，或者solver的取值为"liblinear"，“auto"会默认选择"ovr”。反之，则会选择"nultinomial"。
注意：默认值将在0.22版本中从"ovr"更改为"auto"。

我们之前提到的梯度下降法，只是求解逻辑回归参数 的一种方法，并且我们只讲解了求解二分类变量的参数时的各种原理。sklearn为我们提供了多种选择，让我们可以使用不同的求解器来计算逻辑回归。求解器的选择，由参数"solver"控制，共有五种选择。其中“liblinear”是二分类专用，也是现在的默认求解器。

来看看鸢尾花数据集上，multinomial和ovr的区别怎么样：

from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression as LR

iris = load_iris()
iris.target #三分类数据集

for multi_class in (‘multinomial’, ‘ovr’):

lf = LR(solver='sag', max_iter=100, random_state=42,
                         multi_class=multi_class).fit(iris.data, iris.target)
print("training score : %.3f (%s)" % (lf.score(iris.data, iris.target), multi_class))

#打印两种multi_class模式下的训练分数
#%的用法，用%来代替打印的字符串中，想由变量替换的部分。%.3f表示，保留三位小数的浮点数。%s表示，字符串。
#字符串后的%后使用元祖来容纳变量，字符串中有几个%，元祖中就需要有几个变量

2.5 样本不平衡与参数class_weight

样本不平衡是指在一组数据集中，标签的一类天生占有很大的比例，或误分类的代价很高，即我们想要捕捉出某种特定的分类的时候的状况。

什么情况下误分类的代价很高？例如，我们现在要对潜在犯罪者和普通人进行分类，如果没有能够识别出潜在犯罪者，那么这些人就可能去危害社会，造成犯罪，识别失败的代价会非常高，但如果，我们将普通人错误地识别成了潜在犯罪者，代价却相对较小。所以我们宁愿将普通人分类为潜在犯罪者后再人工甄别，但是却不愿将潜在犯罪者分类为普通人，有种"宁愿错杀不能放过"的感觉。

再比如说，在银行要判断“一个新客户是否会违约”，通常不违约的人vs违约的人会是99：1的比例，真正违约的人其实是非常少的。这种分类状况下，即便模型什么也不做，全把所有人都当成不会违约的人，正确率也能有99%，这使得模型评估指标变得毫无意义，根本无法达到我们的“要识别出会违约的人”的建模目的。

因此我们要使用参数class_weight对样本标签进行一定的均衡，给少量的标签更多的权重，让模型更偏向少数类，向捕获少数类的方向建模。该参数默认None，此模式表示自动给与数据集中的所有标签相同的权重，即自动1：1。当误分类的代价很高的时候，我们使用”balanced“模式，我们只是希望对标签进行均衡的时候，什么都不填就可以解决样本不均衡问题。

但是，sklearn当中的参数class_weight变幻莫测，大家用模型跑一跑就会发现，我们很难去找出这个参数引导的模型趋势，或者画出学习曲线来评估参数的效果，因此可以说是非常难用。我们有着处理样本不均衡的各种方法，其中主流的是采样法，是通过重复样本的方式来平衡标签，可以进行上采样（增加少数类的样本），比如SMOTE，或者下采样（减少多数类的样本）。对于逻辑回归来说，上采样是最好的办法。在案例中，会给大家详细来讲如何在逻辑回归中使用上采样。