机器学习--sklearn之逻辑回归
目录
- 线性回归
- Sigmoid函数
- 逻辑回归
- 逻辑回归的损失函数
- 正则化
-
-
- L1正则化
- L2正则化
- L1正则化和L2正则化的区别
-
- 梯度下降法
-
-
- 梯度下降法的代数方式描述
-
-
- 先决条件
- 算法相关参数初始化
- 算法过程
-
- 梯度下降法的矩阵方式描述
-
-
- 先决条件
- 算法相关参数初始化
- 算法过程
-
-
- 梯度下降法分类
-
-
- 批量梯度下降法BGD
- 随机梯度下降法SGD
- 小批量梯度下降法MBGD
- 总结
-
- 梯度下降的算法调优
- python中实现逻辑回归
线性回归
提到逻辑回归我们不得不提一下线性回归，逻辑回归和线性回归同属于广义线性模型，逻辑回归就是用线性回归模型的预测值去拟合真实标签的的对数几率（一个事件的几率（odds）是指该事件发生的概率与不发生的概率之比，如果该事件发生的概率是 P P P，那么该事件的几率是 P 1 − P \frac{P}{1-P} 1−PP，对数几率就是 l o g P 1 − P log\frac{P}{1-P} log1−PP）。
逻辑回归和线性回归本质上都是得到一条直线，不同的是，线性回归的直线是尽可能去拟合输入变量X的分布，使得训练集中所有样本点到直线的距离最短；而逻辑回归的直线是尽可能去拟合决策边界，使得训练集样本中的样本点尽可能分开。因此，两者的目的是不同的。
线性回归方程：
y = w x + b y=wx+b y=wx+b
此处，y为因变量，x为自变量。在机器学习中y是标签，x是特征。
Sigmoid函数
我们想要的函数应该是，能接受所有的输入然后预测出类别。例如在二分类的情况下，函数能输出0或1。那拥有这 类性质的函数称为海维赛德阶跃函数（Heaviside step function），又称之为单位阶跃函数（如下图所示）。
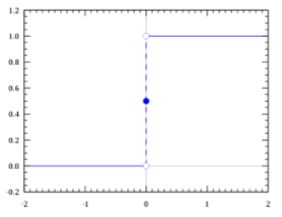
单位阶跃函数的问题在于：在0点位置该函数从0瞬间跳跃到1，这个瞬间跳跃过程很难处理（不好求导）。幸运的是，Sigmoid函数也有类似的性质，且数学上更容易处理。
Sigmoid函数公式：
σ ( x ) = 1 1 + e − x \sigma_{(x)}=\frac{1}{1+e^{-x}} σ(x)=1+e−x1
其图像为：
逻辑回归
通过将线性模型和Sigmoid函数结合，我们可以得到逻辑回归的公式：
y = 1 1 + e − ( ω x + b ) y=\frac{1}{1+e^{-(\omega x+b)}} y=1+e−(ωx+b)1
这样一来，y的取值范围就是（0,1）。
对于二项回归：
对于多项回归：
逻辑回归的损失函数
LR损失函数为：
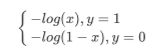我们把这两个损失函数综合起来：
y就是标签，分别取0和1。
对于m个样本，总的损失函数为对数损失函数：
这个式子中，m是样本数，y是标签，取值0或1，i表示第i个样本，p(x)表示预测的输出，是一个概率。
讨论：
损失函数为什么是对数损失函数（交叉熵），而不是MSE？ 假设目标函数是MSE而不是交叉熵，即
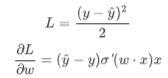这里Sigmoid的导数项：
根据 ω \omega ω的初始化，导数值可能很小（Sigmoid函数在输入较大时的梯度）而导致收敛变慢，而训练途中也可能因为该值过小而提早终止训练。
另一方面，对数损失函数的梯度如下，当模型输出概率偏离于真实概率时，梯度较大，加快训练速度，当拟合值接近于真实概率时训练速度变缓慢，没有MSE存在的问题。
正则化
不过当损失过于小的时候，也就是模型能够拟合绝大部分的数据，这时候就容易出现过拟合。为了防止过拟合，我们会引入正则化。
L1正则化
Lasso 回归，相当于为模型添加了这样一个先验知识： ω \omega ω服从零均值拉普拉斯分布。
拉普拉斯分布：
其中μ,b为常数，且μ>0。
由于引入了先验知识，所以似然函数写成：
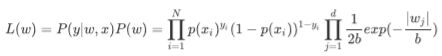取对数再取负，得到目标函数：
等价于原始的cross−entropy后面加上了L1正则，因此L1正则的本质其实是为模型增加了“模型参数服从零均值拉普拉斯分布”这一先验知识。
L2正则化
Ridge 回归，相当于为模型添加了这样一个先验知识： ω \omega ω服从零均值正态分布。
正态分布公式：
由于引入了先验知识，所以似然函数写成：
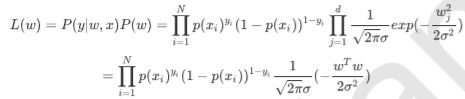取对数再取负，得到目标函数：
等价于原始的cross−entropy后面加上了L2正则，因此L2正则的本质其实是为模型增加了“模型参数服从零均值正态分布”这一先验知识。
L1正则化和L2正则化的区别
- 两者引入的关于模型参数的先验知识不一样，L1是拉普拉斯分布，L2是正态分布。
- L1偏向于使模型参数变得稀疏(但实际上并不那么容易)，L2偏向于使模型每一个参数都很小，但是更加稠密，从而防止过拟合。
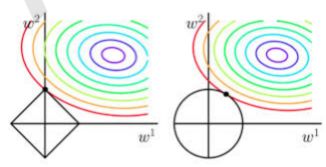
为什么L1偏向于稀疏，L2偏向于稠密呢？ 看下面两张图，每一个圆表示loss的等高线，即在该圆上loss都是相同的，可以看到L1更容易在坐标轴上达到，而L2则容易在象限里达到。
梯度下降法
梯度下降法的代数方式描述
先决条件
确认优化模型的假设函数和损失函数。 比如对于线性回归，假设函数表示为 h θ ( x 1 , x 2 , … … , x n ) = θ 0 + θ 1 x 1 + … … + θ n x n h_{\theta}(x_1,x_2,……,x_n)=\theta_0+\theta_1x_1+……+\theta_nx_n hθ(x1,x2,……,xn)=θ0+θ1x1+……+θnxn，其中 θ i ( i = 0 , 1 , … … , n ) \theta_i \ (i=0,1,……,n) θi (i=0,1,……,n)为模型参数， x i ( i = 0 , 1 , … … , n ) x_i \ (i=0,1,……,n) xi (i=0,1,……,n)为每个样本的n个特征值。这个表达式可以简化，我们增加一个特征 x 0 = 1 x_0=1 x0=1，这样 h θ ( x 1 , x 2 , … … , x n ) = ∑ i = 0 n θ i x i h_{\theta}(x_1,x_2,……,x_n)=\sum_{i=0}^{n}\theta_ix_i hθ(x1,x2,……,xn)=∑i=0nθixi。 同样是线性回归，对应于上面的假设函数，损失函数为（此处在损失函数之前加上 1 2 m \frac{1}{2m} 2m1，主要是为了修正损失函数让计算公式结果更加美观）：
算法相关参数初始化
主要是初始化 θ i ( i = 0 , 1 , … … , n ) \theta_i \ (i=0,1,……,n) θi (i=0,1,……,n)，算法终止距离 ϵ \epsilon ϵ以及步长 α \alpha α。在没有任何先验知识的时候， 我们比较倾向于将所有的 θ \theta θ初始化为0，将步长初始化为1。在调优的时候再进行优化。
算法过程
(1).确定当前位置的损失函数的梯度，对于 θ i \theta_i θi，其梯度表达式如下：
(2).用步长乘以损失函数的梯度，得到当前位置下降的距离，即：
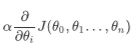(3).确定是否对于所有的 θ i \theta_i θi，梯度下降的距离都小于 ϵ \epsilon ϵ，如果小于 ϵ \epsilon ϵ则算法终止，当前所有的 θ i ( i = 0 , 1 , … … , n ) \theta_i \ (i=0,1,……,n) θi (i=0,1,……,n)即为终结果。否则进入步骤4。
(4).更新所有的KaTeX parse error: Expected group after '_' at position 7: \theta_̲，对于 θ i \theta_i θi，其更新表达式如下。更新完毕后继续转入步骤1。
下面用线性回归的例子来具体描述梯度下降。假设我们的样本是：
损失函数如前面先决条件所述：
则在算法过程步骤1中对于 θ i \theta_i θi的偏导数计算如下：
由于样本中没有 x 0 x_0 x0上式中令所有的 x 0 ( j ) x_0^{(j)} x0(j)为1。步骤4中 θ i \theta_i θi的更新表达式如下：
梯度下降法的矩阵方式描述
先决条件
需要确认优化模型的假设函数和损失函数。对于线性回归，假设函数 h θ ( x 1 , x 2 , … … , x n ) = θ 0 + θ 1 x 1 + … … + θ n x n h_{\theta}(x_1,x_2,……,x_n)=\theta_0+\theta_1x_1+……+\theta_nx_n hθ(x1,x2,……,xn)=θ0+θ1x1+……+θnxn的矩阵表达方式为：
其中，假设函数 h θ ( x ) h_{\theta}(\bf x) hθ(x)为 m ∗ 1 m*1 m∗1的向量, θ \theta θ为 ( n + 1 ) ∗ 1 (n+1)*1 (n+1)∗1的向量，里面有n个代数法的模型参数。 X \bf X X为 m ∗ ( n + 1 ) m*(n+1) m∗(n+1)维的矩阵。 m代表样本的个数，n+1代表样本的特征数。 损失函数的表达式为：
其中 Y \bf Y Y是样本的输出向量，维度为 m ∗ 1 m*1 m∗1。
算法相关参数初始化
在没有任何先验知识的时候， 我们比较倾向于将所有的 θ \theta θ初始化为0，将步长初始化为1。在调优的时候再进行优化。
算法过程
(1).确定当前位置的损失函数的梯度，对于 θ \theta θ向量，其梯度表达式如下：
(2).用步长乘以损失函数的梯度，得到当前位置下降的距离，即 α ∂ ∂ θ J ( θ ) \alpha\frac{\partial} {\partial\theta}J(\theta) α∂θ∂J(θ)对应于前面登山例子中的某一步。
(3).确定 θ \mathbf\theta θ向量里面的每个值,梯度下降的距离都小于 ε \varepsilon ε，如果小于 ε \varepsilon ε则算法终止，当前 θ \mathbf\theta θ向量即为终结果。否则进入步骤4.
(4).更新 θ \theta θ向量，其更新表达式如下。更新完毕后继续转入步骤1.
还是用线性回归的例子来描述具体的算法过程。 损失函数对于 向量的偏导数计算如下：
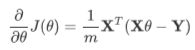步骤4中 θ \theta θ向量的更新表达式如下：
可以看到矩阵法要简洁很多。这里面用到了矩阵求导链式法则，和下面两个矩阵求导的公式：
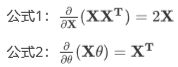
梯度下降法分类
批量梯度下降法BGD
批量梯度下降法（Batch Gradient Descent，BGD）是梯度下降法常用的形式，具体做法也就是在更新参数时使用所有的样本来进行更新。
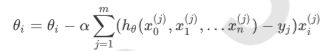由于我们有m个样本，这里求梯度的时候就用了所有样本的梯度数据。
随机梯度下降法SGD
随机梯度下降法，其实和批量梯度下降法原理类似，区别在与求梯度时没有用所有的m个样本的数据，而是仅仅选取一个样本j来求梯度。对应的更新公式是：
随机梯度下降法和批量梯度下降法是两个极端，一个采用所有数据来梯度下降，一个用一个样本来梯度下降。自然各自的优缺点都非常突出。对于训练速度来说，随机梯度下降法由于每次仅仅采用一个样本来迭代，训练速度很快，而批量梯度下降法在样本量很大的时候，训练速度不能让人满意。对于准确度来说，随机梯度下降法用于仅仅用一个样本决定梯度方向，导致解很有可能不是最优。对于收敛速度来说，由于随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不能很快的收敛到局部优解。 但值得一提的是，随机梯度下降法在处理非凸函数优化的过程当中有非常好的表现，由于其下降方向具有一定随机性，因此能很好的绕开局部优解，从而逼近全局最优解。
小批量梯度下降法MBGD
小批量梯度下降法是批量梯度下降法和随机梯度下降法的折衷，也就是对于m个样本，我们采用x个子样本来迭代，1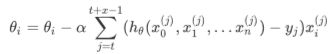
总结
BGD会获得全局优解，缺点是在更新每个参数的时候需要遍历所有的数据，计算量会很大，并且会有很多的冗余计算，导致的结果是当数据量大的时候，每个参数的更新都会很慢。
SGD以高方差频繁更新，优点是使得SGD会跳到新的和潜在更好的局部优解，缺点是使得收敛到局部优解的过程更加的复杂。
MBGD降结合了BGD和SGD的优点，每次更新的时候使用n个样本。减少了参数更新的次数，可以达到更加稳定收敛结果，一般在深度学习当中可以采用这种方法，将数据一个batch一个batch的送进去训练。
梯度下降的算法调优
- 算法的步长选择。步长的选择实际上取值取决于数据样本，可以多取一些值，从大到小，分别运行算法，看看迭代效果，如果损失函数在变小，说明取值有效，否则要增大步长。前面说了，步长太大，会导致迭代过快，甚至有可能错过最优解。步长太小，迭代速度太慢，很长时间算法都不能结束。所以算法的步长需要多次运行后才能得到一个较优的值。
- 算法参数的初始值选择。 初始值不同，获得的最小值也有可能不同，因此梯度下降求得的只是局部最小值； 当然如果损失函数是凸函数则一定是优解。由于有局部最优解的风险，需要多次用不同初始值运行算法，选择损失函数小化的初值。
- 标准化。由于样本不同特征的取值范围不一样，可能导致迭代很慢，为了减少特征取值的影响，可以对特征数据标准化，也就是对于每个特征x，求出它的期望和标准差，然后转化为：
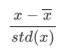这样一来，特征的新期望为0，新方差为1，收敛速度可以大大加快。
python中实现逻辑回归
from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score#精确性分数
data = load_breast_cancer()#乳腺癌数据集
X = data.data
y = data.target
X.data.shape#(569, 30)
lrl1 = LR(penalty="l1",solver="liblinear",C=0.5,max_iter=1000)
lrl2 = LR(penalty="l2",solver="liblinear",C=0.5,max_iter=1000)
#逻辑回归的重要属性coef_，查看每个特征所对应的参数（theta）
lrl1 = lrl1.fit(X,y)
lrl1.coef_
(lrl1.coef_ != 0).sum(axis=1)#array([10]) 30个特征中有10个特征的系数不为0
lrl2 = lrl2.fit(X,y)
lrl2.coef_
那么，L1和L2正则化哪个更好呢？
l1 = []
l2 = []
l1test = []
l2test = []
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
for i in np.linspace(0.05,1.5,19):
lrl1 = LR(penalty="l1",solver="liblinear",C=i,max_iter=1000)
lrl2 = LR(penalty="l2",solver="liblinear",C=i,max_iter=1000)
lrl1 = lrl1.fit(Xtrain,Ytrain)
l1.append(accuracy_score(lrl1.predict(Xtrain),Ytrain))
l1test.append(accuracy_score(lrl1.predict(Xtest),Ytest))
lrl2 = lrl2.fit(Xtrain,Ytrain)
l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain))
l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest))
graph = [l1,l2,l1test,l2test]
color = ["green","black","lightgreen","gray"]
label = ["L1","L2","L1test","L2test"]
plt.figure(figsize=(6,6))
for i in range(len(graph)):
plt.plot(np.linspace(0.05,1.5,19),graph[i],color[i],label=label[i])
plt.legend(loc=4) #图例的位置在哪里?----4表示，在右下角
plt.show()