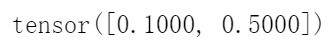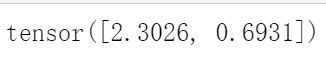【线性神经网络】softmax回归
one - hot 编码
一般用于分类问题,其特征是离散的
很简单,用n个状态表示表示n个特征,其中只有一个状态取值为1,其他全为0
交叉熵
使用真实概率与预测概率的区别来作为损失
损失函数
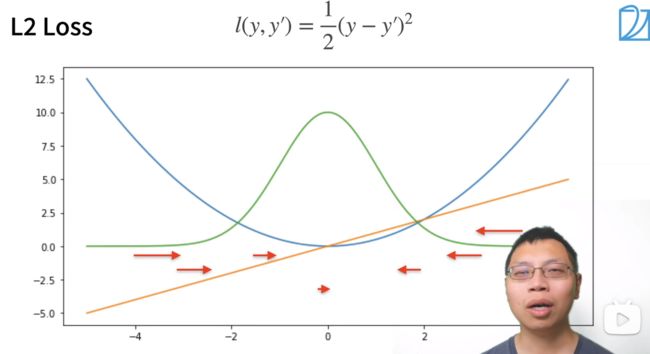
均方损失 L2 Loss
绿色曲线是似然函数,黄色为梯度
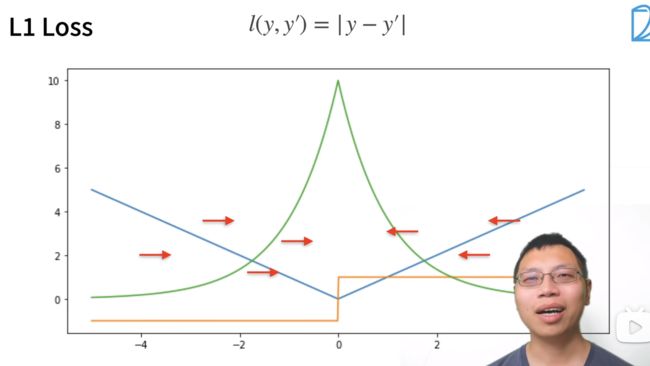
当离原点较远的时候,对参数的更新幅度可能较大,这里引出L1 Loss
绝对值损失 L1 Loss
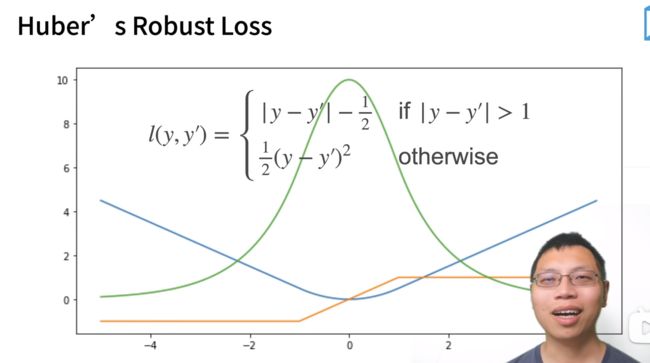
Huber's Rubust Loss
结合L1 Loss 和 L2 Loss的损失函数
Softmax从0实现
读数据
import torch
from IPython import display
from d2l import torch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)数据集是Fashion-MNIST,10个种类的图像,每个种类6000张,训练集为60000,测试集为10000,批量大小256
num_inputs = 784
num_outputs = 10
W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)每张图片为28 * 28,展开为784维向量,输出层为10个种类
这里权重W为(784,10)的矩阵,输入数据x为长度784的向量,对于O(1 -> 10),每个Oj对应
Oj = < W[j],X > + bj,所以W的列数为num_outputs,也就是O的个数(种类)
显然,b也要和O对应
softmax
顾名思义,softmax与hardmax对应,常规对序列求最值就是hardmax,而在分类中,采用one hot编码,以及引入置信度,根据softmax引入的e的指数,我们只关心是否能让正确类别的预测值以及置信度足够大,而不关心非正确类别。模型能够把真正的类别和其他的类别拉开一个距离。
def softmax(X):
X_exp = torch.exp(X)
partition = X_exp.sum(1, keepdim=True)
return X_exp / partition # 这里应用了广播机制模型
def net(X):
return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)交叉熵
y = torch.tensor([0, 2])
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y_hat[[0, 1], y]y记录真实类别的索引,y_hat[ [0,1] , y ]返回的是第一组[0.1,0.3,0.6]的真实类别索引的元素0.1和第二组的0.5
def cross_entropy(y_hat, y):
return - torch.log(y_hat[range(len(y_hat)), y])
cross_entropy(y_hat, y)softmax简洁实现
导入
import torch
from torch import nn
from d2l import torch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)初始化模型参数
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights);nn.Flatten()用来调整网络输入的形状
trainer = torch.optim.SGD(net.parameters(), lr=0.1)损失函数
loss = nn.CrossEntropyLoss(reduction='none')优化算法
trainer = torch.optim.SGD(net.parameters(), lr=0.1)训练
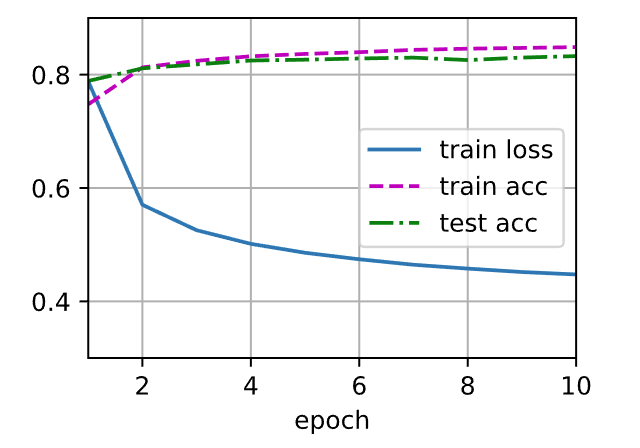
num_epochs = 10
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)